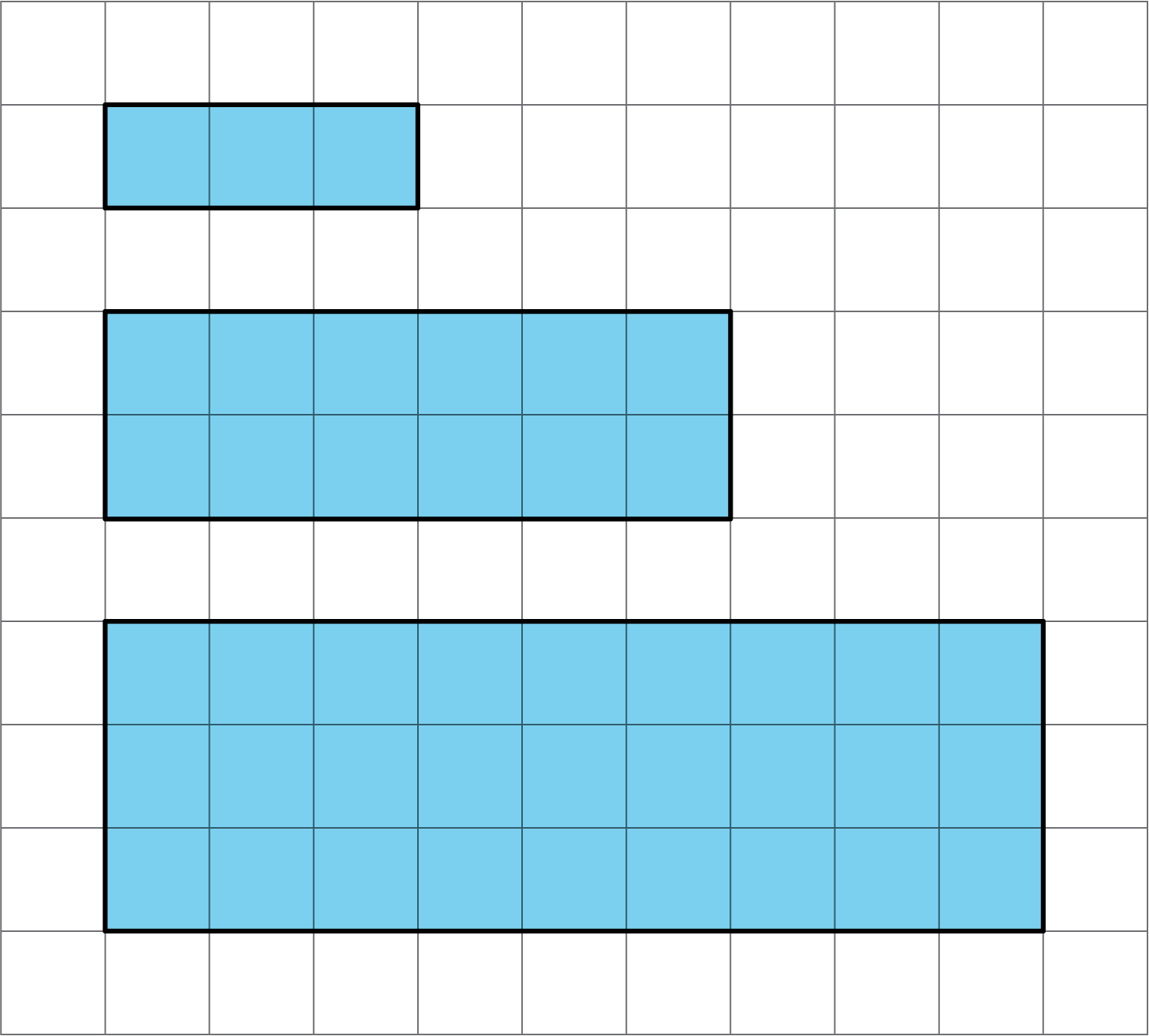
8.1: Notice and Wonder: Patterns with Rectangles
Let’s develop methods for deciding if a relationship is proportional.

The other day you worked with converting meters, centimeters, and millimeters. Here are some more unit conversions.
| temperature $(^\circ\text{C})$ | temperature $(^\circ\text{F})$ | |
|---|---|---|
| row 1 | 20 | |
| row 2 | 4 | |
| row 3 | 175 |
| length (in) | length (cm) | |
|---|---|---|
| row 1 | 10 | |
| row 2 | 8 | |
| row 3 | 3$\frac12$ |
Here are some cubes with different side lengths. Complete each table. Be prepared to explain your reasoning.
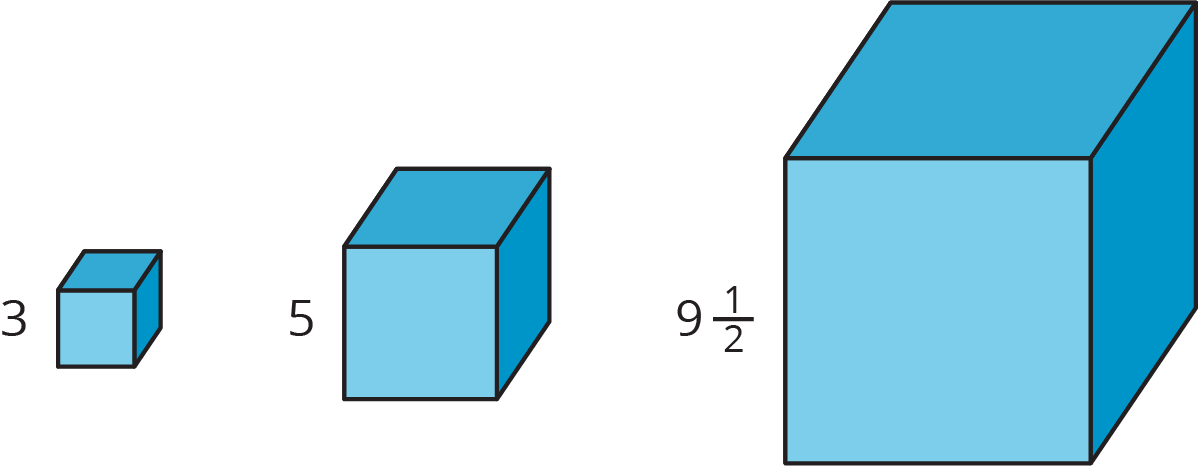
| row 1 | side length |
total edge length |
|---|---|---|
| row 2 | 3 | |
| row 3 | 5 | |
| row 4 | $9\frac12$ | |
| row 4 | $s$ |
| row 1 | side length |
surface area |
|---|---|---|
| row 2 | 3 | |
| row 3 | 5 | |
| row 4 | $9\frac12$ | |
| row 5 | $s$ |
| row 1 | side length |
volume |
|---|---|---|
| row 2 | 3 | |
| row 3 | 5 | |
| row 4 | $9\frac12$ | |
| row 5 | $s$ |
Write equations for the total edge length $E$, total surface area $A$, and volume $V$ of a cube with side length $s$.
Here are six different equations.
$y = 4 + x$
$y = \frac{x}{4}$
$y = 4x$
$y = 4^{x}$
$y = \frac{4}{x}$
$y = x^{4}$

If two quantities are in a proportional relationship, then their quotient is always the same. This table represents different values of $a$ and $b$, two quantities that are in a proportional relationship.
| row 1 | $a$ | $b$ | $\frac{b}{a}$ |
|---|---|---|---|
| row 2 | 20 | 100 | 5 |
| row 3 | 3 | 15 | 5 |
| row 4 | 11 | 55 | 5 |
| row 5 | 1 | 5 | 5 |
Notice that the quotient of $b$ and $a$ is always 5. To write this as an equation, we could say $\frac{b}{a}=5$. If this is true, then $b=5a$. (This doesn’t work if $a=0$, but it works otherwise.)
If quantity $y$ is proportional to quantity $x$, we will always see this pattern: $\frac{y}{x}$ will always have the same value. This value is the constant of proportionality, which we often refer to as $k$. We can represent this relationship with the equation $\frac{y}{x} = k$ (as long as $x$ is not 0) or $y=kx$.
Note that if an equation cannot be written in this form, then it does not represent a proportional relationship.