6.1: Which One Doesn’t Belong: Triangles
Which triangle doesn’t belong?
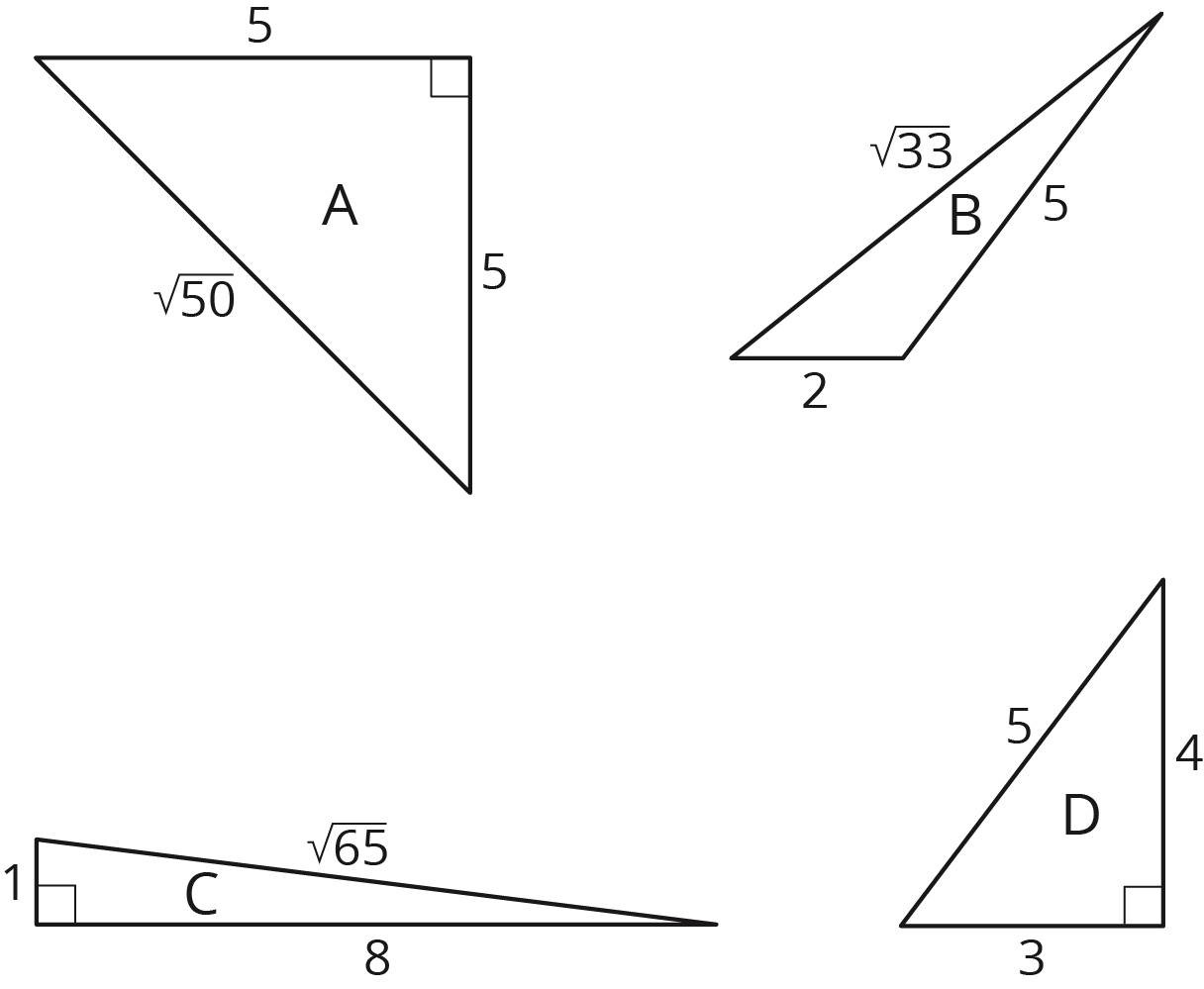
Let’s find triangle side lengths.
Which triangle doesn’t belong?

Complete the tables for these three triangles:
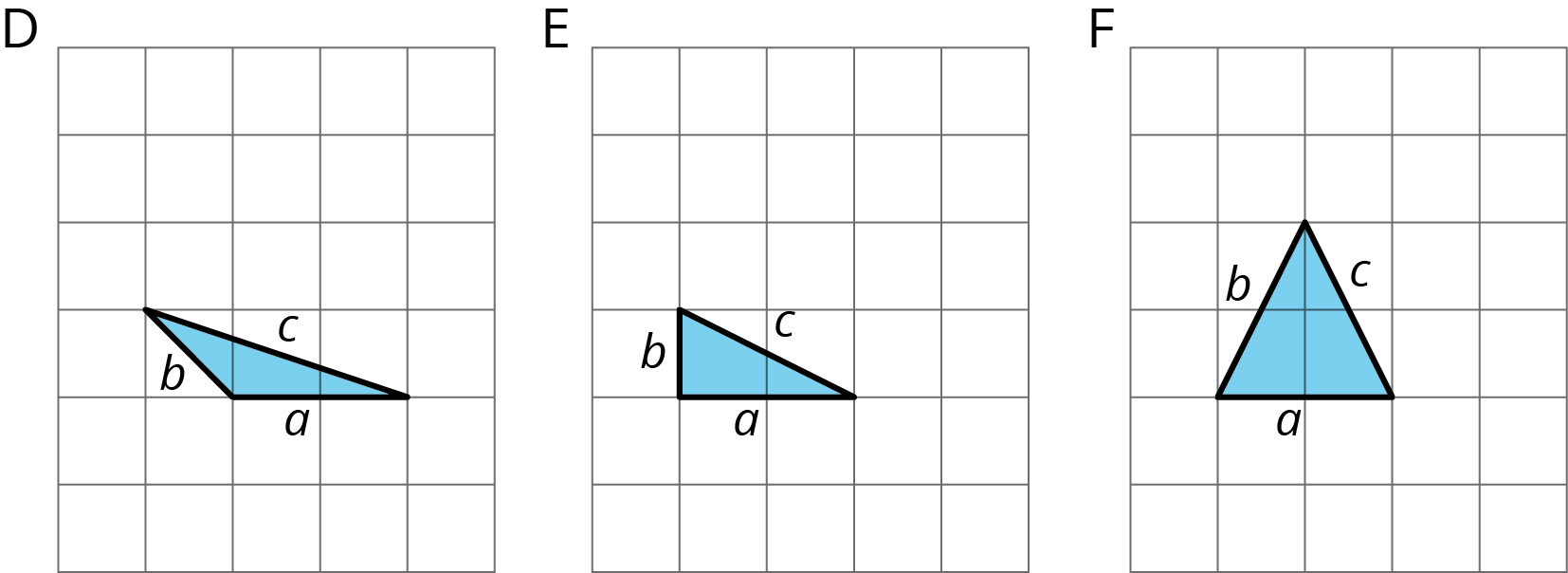
| triangle | \(a\) | \(b\) | \(c\) | |
|---|---|---|---|---|
| row 1 | D | |||
| row 2 | E | |||
| row 3 | F |
| triangle | \(a^2\) | \(b^2\) | \(c^2\) | |
|---|---|---|---|---|
| row 1 | D | |||
| row 2 | E | |||
| row 3 | F |
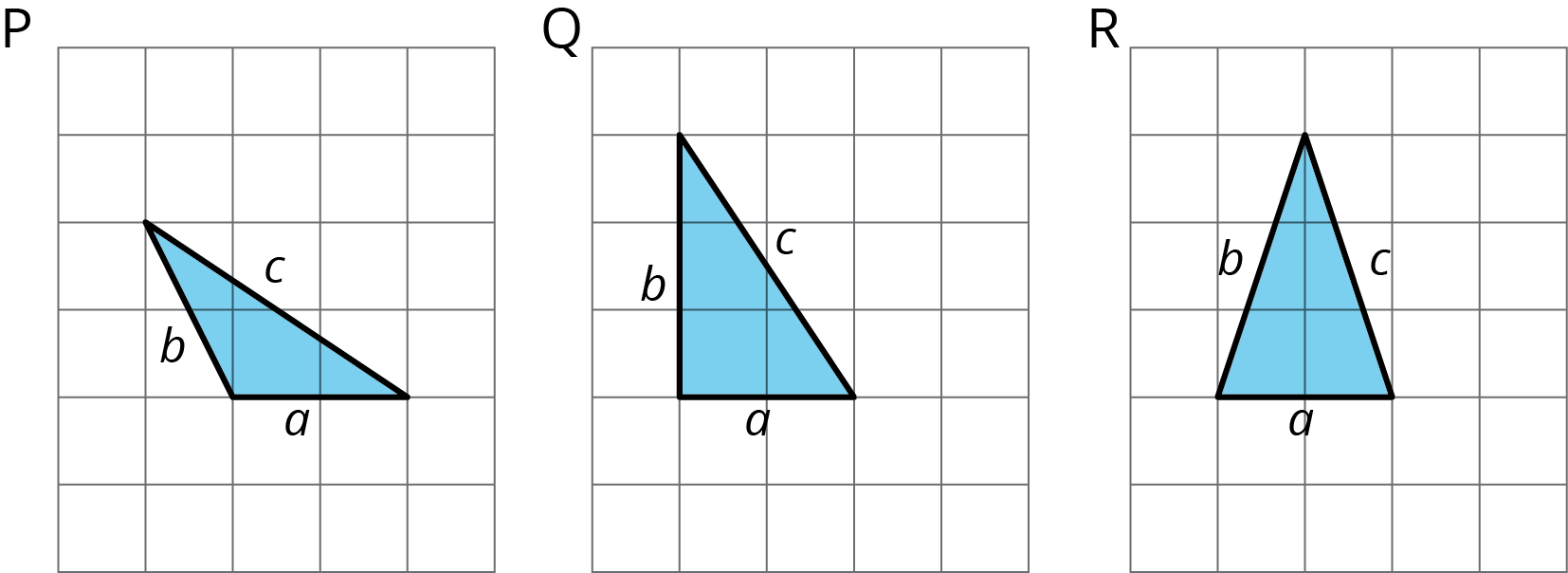
| triangle | \(a\) | \(b\) | \(c\) | |
|---|---|---|---|---|
| row 1 | P | |||
| row 2 | Q | |||
| row 3 | R |
| triangle | \(a^2\) | \(b^2\) | \(c^2\) | |
|---|---|---|---|---|
| row 1 | P | |||
| row 2 | Q | |||
| row 3 | R |



If the four shaded triangles in the figure are congruent right triangles, does the inner quadrilateral have to be a square? Explain how you know.

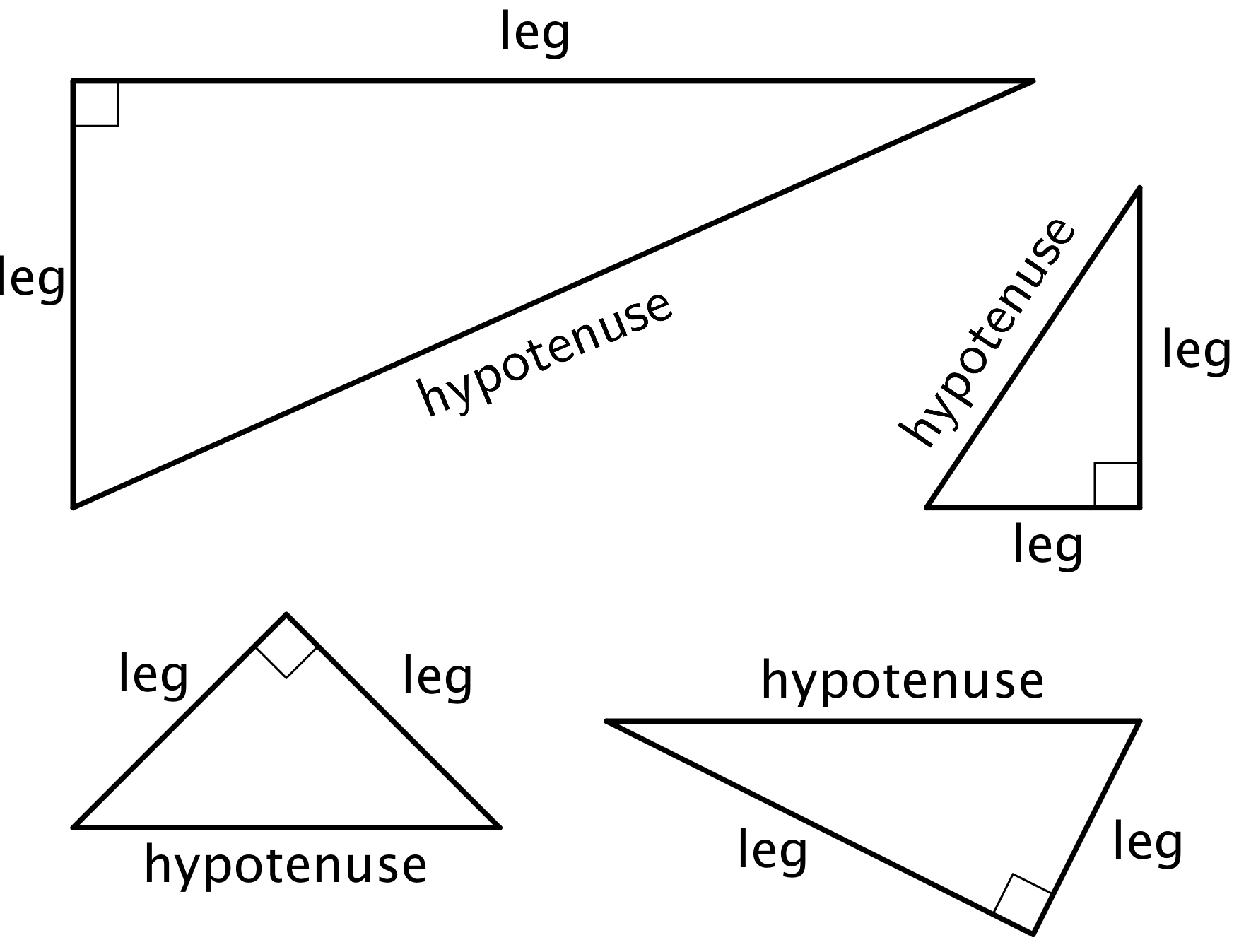
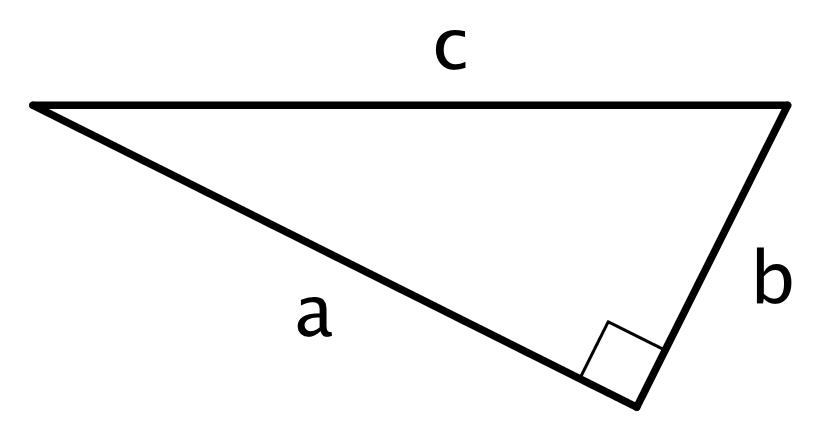
A right triangle is a triangle with a right angle. In a right triangle, the side opposite the right angle is called the hypotenuse, and the two other sides are called its legs. Here are some right triangles with the hypotenuse and legs labeled:
We often use the letters $a$ and $b$ to represent the lengths of the shorter sides of a triangle and $c$ to represent the length of the longest side of a right triangle. If the triangle is a right triangle, then $a$ and $b$ are used to represent the lengths of the legs, and $c$ is used to represent the length of the hypotenuse (since the hypotenuse is always the longest side of a right triangle). For example, in this right triangle, $a=\sqrt{20}$, $b=\sqrt5$, and $c=5$.
Here are some right triangles:

Notice that for these examples of right triangles, the square of the hypotenuse is equal to the sum of the squares of the legs. In the first right triangle in the diagram, $9+16=25$, in the second, $1+16=17$, and in the third, $9+9=18$. Expressed another way, we have $$a^2+b^2=c^2$$ This is a property of all right triangles, not just these examples, and is often known as the Pythagorean Theorem. The name comes from a mathematician named Pythagoras who lived in ancient Greece around 2,500 BCE, but this property of right triangles was also discovered independently by mathematicians in other ancient cultures including Babylon, India, and China. In China, a name for the same relationship is the Shang Gao Theorem. In future lessons, you will learn some ways to explain why the Pythagorean Theorem is true for any right triangle.
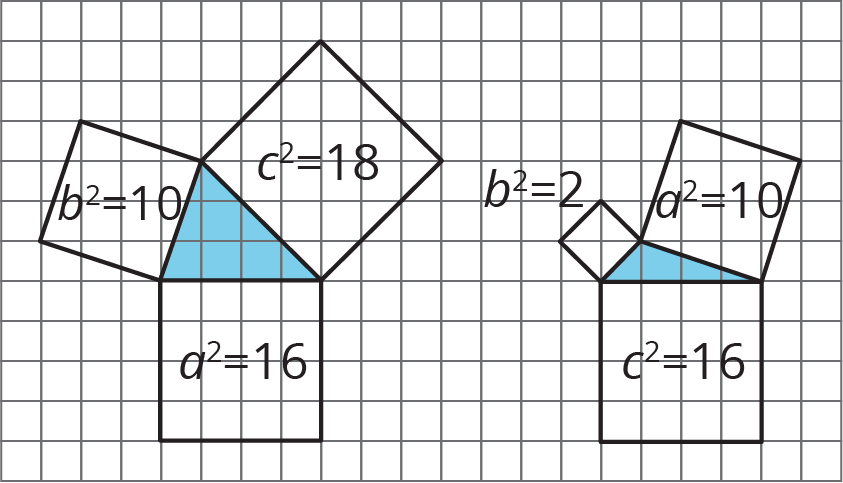
It is important to note that this relationship does not hold for all triangles. Here are some triangles that are not right triangles, and notice that the lengths of their sides do not have the special relationship $a^2+b^2=c^2$. That is, $16+10$ does not equal 18, and $2+10$ does not equal 16.
The Pythagorean Theorem is a name for the property of all right triangles that the square of the hypotenuse is equal to the sum of the squares of the legs. It is often expressed as $a^2+b^2=c^2$.
In a right triangle, the side opposite the right angle is called the hypotenuse.
In a right triangle, the sides that are adjacent to the right angle are called the legs.