What are Ratios?
A ratio is an association between two or more quantities. For example, say we have a drink recipe made with cups of juice and cups of soda water. Ratios can be represented with diagrams like those below.

Here are some correct ways to describe this diagram:
- The ratio of cups of juice to cups of soda water is $6:4$.
- The ratio of cups of soda water to cups of juice is 4 to 6.
- There are 3 cups of juice for every 2 cups of soda water.
The ratios $6:4$, $3:2$, and $12:8$ are equivalent because each ratio of juice to soda water would make a drink that tastes the same.
Here is a task to try with your student:
There are 4 horses in a stall. Each horse has 4 legs, 1 tail, and 2 ears.
- Draw a diagram that shows the ratio of legs, tails, and ears in the stall.
-
Complete each statement.
- The ratio of ________ to ________ to ________ is ________ : ________ : ________.
- There are ________ ears for every tail. There are ________ legs for every ear.
Solution:
- Answers vary. Sample response:

- Answers vary. Sample response: The ratio of legs to tails to ears is $16:4:8$. There are 2 ears for every tail. There are 2 legs for every ear.
Representing Equivalent Ratios
There are different ways to represent ratios.
Let’s say the 6th grade class is selling raffle tickets at a price of \$6 for 5 tickets. Some students may use diagrams with shapes to represent the situation. For example, here is a diagram representing 10 tickets for \$12.

Drawing so many shapes becomes impractical. Double number line diagrams are easier to work with. The one below represents the price in dollars for different numbers of raffle tickets all sold at the same rate of \$12 for 10 tickets.

Here is a task to try with your student:
Raffle tickets cost \$6 for 5 tickets.
- How many tickets can you get for \$90?
- What is the price of 1 ticket?
Solution:
- 75 tickets. Possible strategies: Extend the double number line shown and observe that \$90 is lined up with 75 tickets. Or, since 90 is 6 times 15, compute 5 times 15.
- \$1.20. Possible strategies: Divide the number line into 5 equal intervals, as shown. Reason that the price in dollars of 1 ticket must be $6 \div 5.$

Solving Ratio and Rate Problems
Over the course of this unit, your student has learned to use the language of ratios and to work with ratios using representations like diagrams and double number lines. In the final sections of the unit, they use tables to organize equivalent ratios. Double number lines are hard to use in problems with large amounts. Let’s think about an example we saw before: the 6th grade class is selling raffle tickets at a price of \$6 for 5 tickets. If we tried to extend the double number line below to represent the price of 300 raffle tickets, it would take 5 times more paper!

A table is a better choice to represent this situation. Tables of equivalent ratios are useful because you can arrange the rows in any order. For example, a student may find the price for 300 raffle tickets by making the table shown.
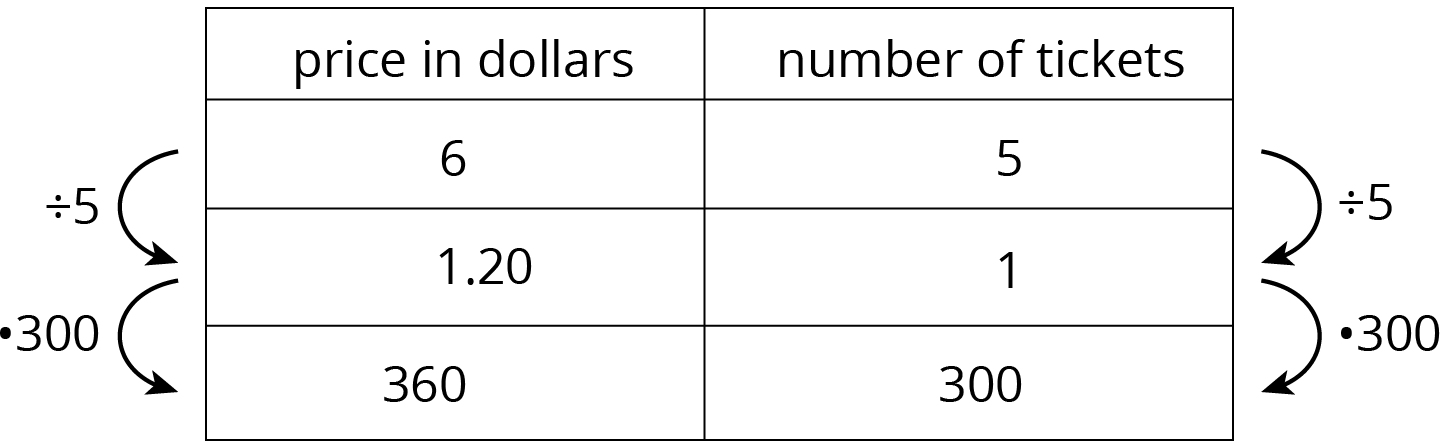
Although students can choose any representation that helps them solve a problem, it is important that they get comfortable with tables because they are used for a variety of purposes throughout high school and college mathematics courses.
Here is a task to try with your student:
At a constant speed, a train travels 45 miles in 60 minutes. At this rate, how far does the train travel in 12 minutes? If you get stuck, consider creating a table.
Solution:
9 miles. Possible strategy:
| time in minutes | distance in miles | |
|---|---|---|
| row 1 | 60 | 45 |
| row 2 | 1 | 0.75 |
| row 3 | 12 | 9 |