12.1: Covering the Cabinet (Part 1)
Your teacher will show you a video about a cabinet or some pictures of it.
Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?
Let’s cover the surfaces of some three-dimensional objects.
Your teacher will show you a video about a cabinet or some pictures of it.
Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?
Earlier, you learned about a cabinet being covered with sticky notes.
Here is a rectangular prism built from 12 cubes:

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units.
The applet has 12 blocks, too. They are all in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. To use a block, drag the red point to move it. Click on the red points to change from left/right movement to up/down movement.
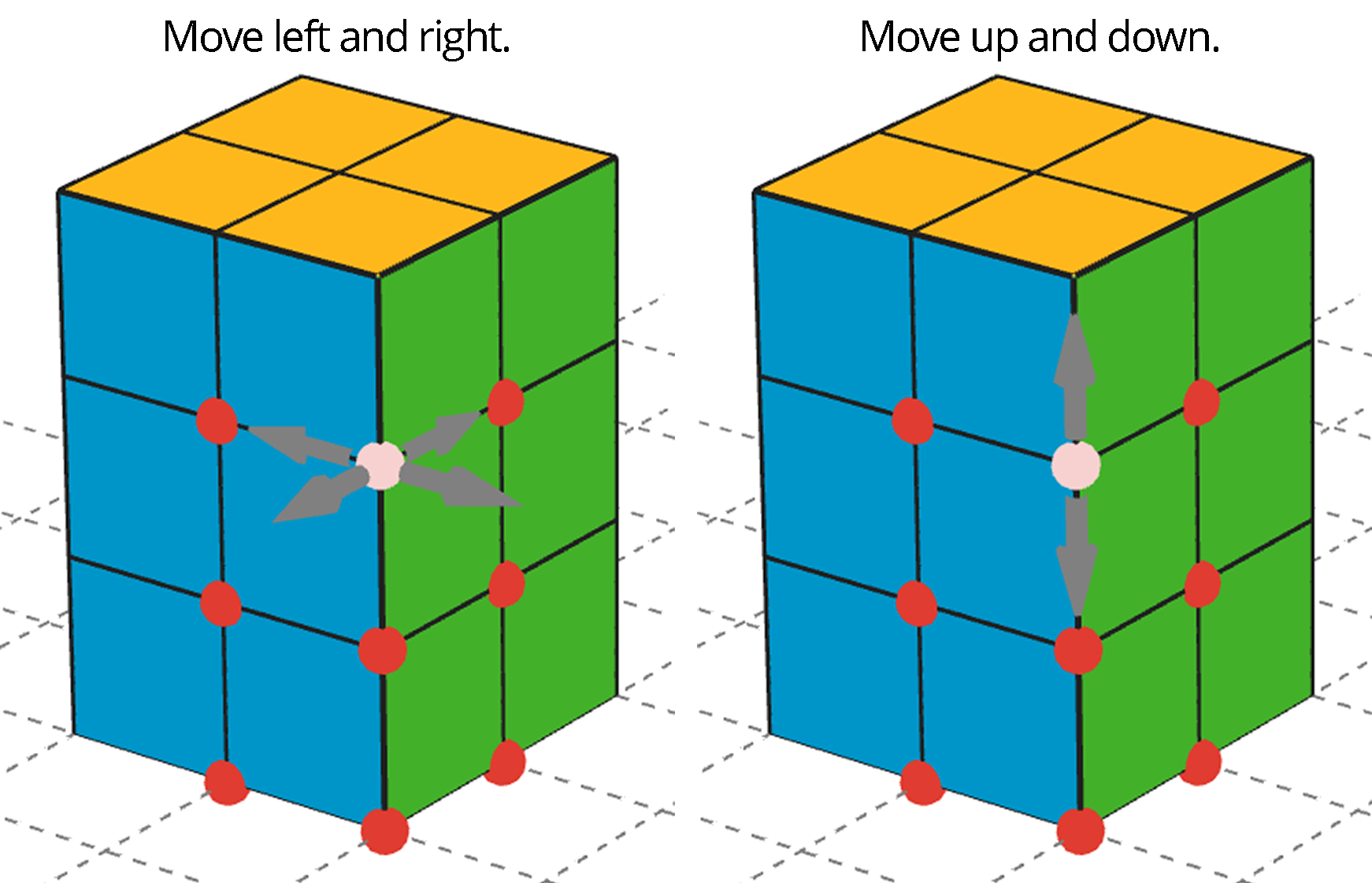
Use all 12 cubes to build a different rectangular prism (with different edge lengths than shown in the prism here). You can turn the view to see all of the faces of your figure.
For example, a rectangular prism has six faces. The surface area of the prism is the total of the areas of the six rectangular faces.

So the surface area of a rectangular prism that has edge-lengths 2 cm, 3 cm, and 4 cm has a surface area of $$(2\boldcdot 3)+ (2\boldcdot 3) + (2\boldcdot 4) + (2\boldcdot 4) + (3\boldcdot 4) + (3\boldcdot 4)$$ or 52 square centimeters.
The surface area (in square units) is the number of unit squares it takes to cover all the surfaces of a three-dimensional figure without gaps or overlaps.
Any flat surface on a three-dimensional figure is a face.