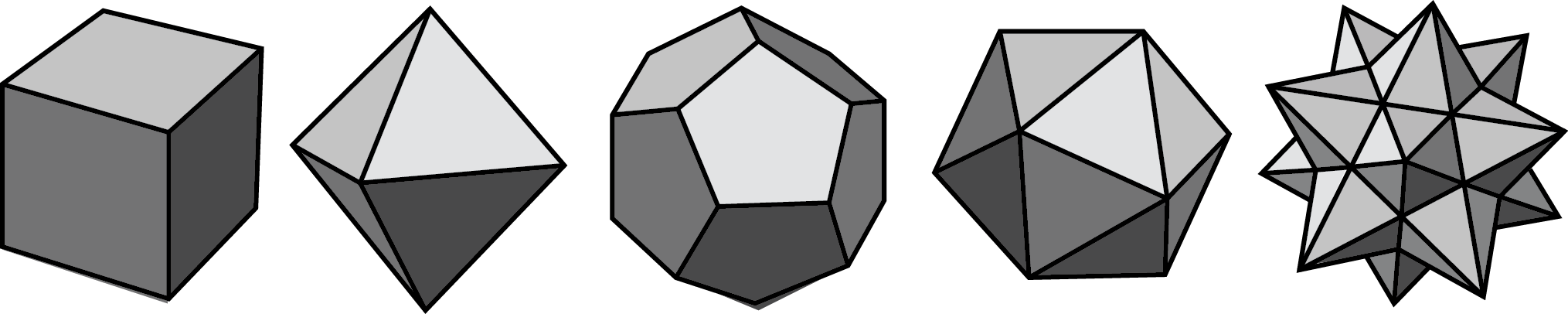
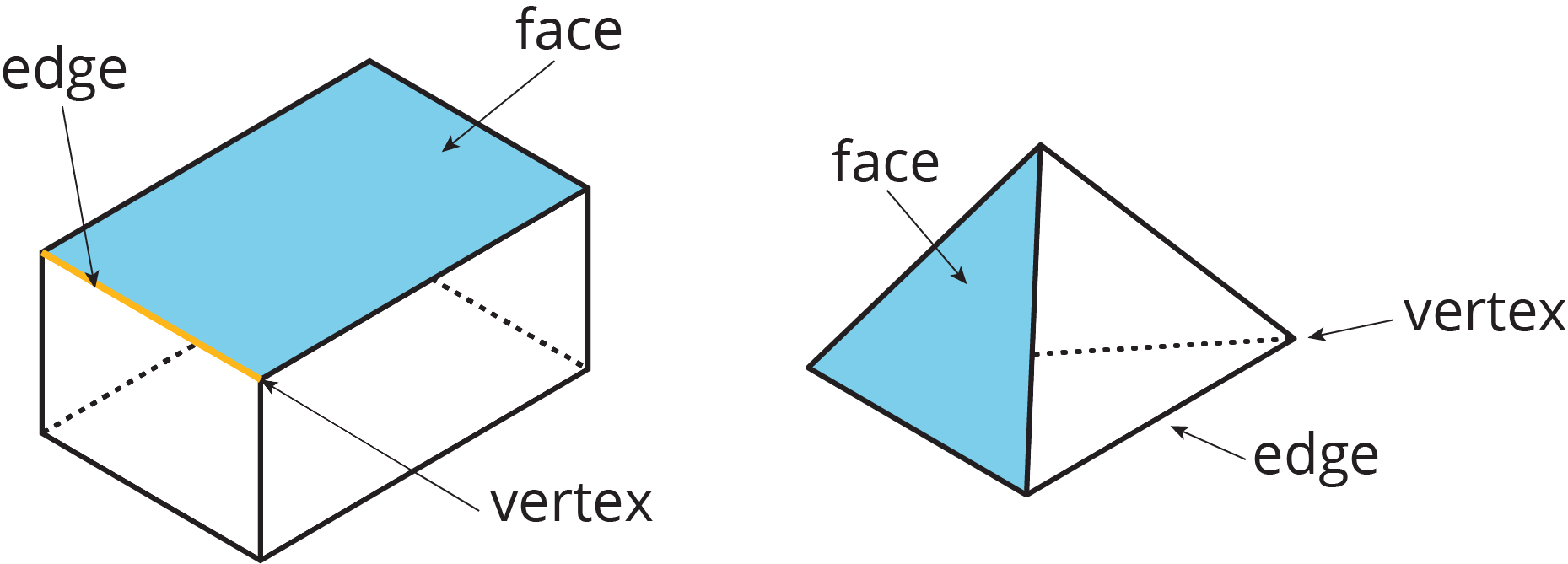
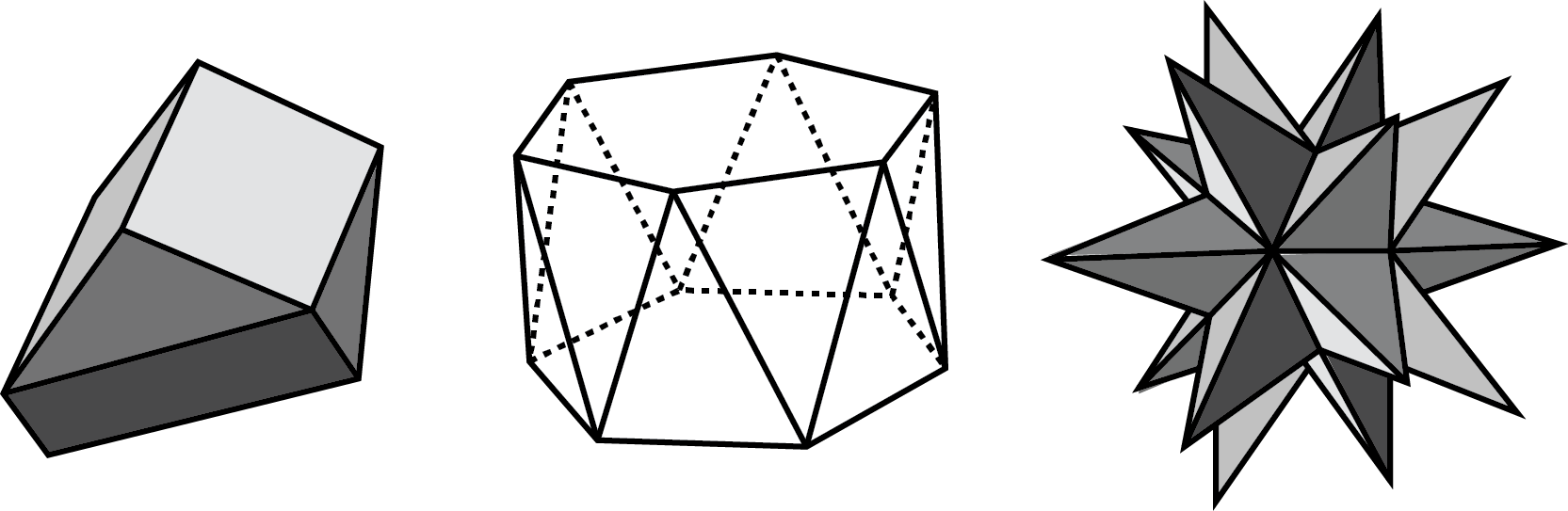
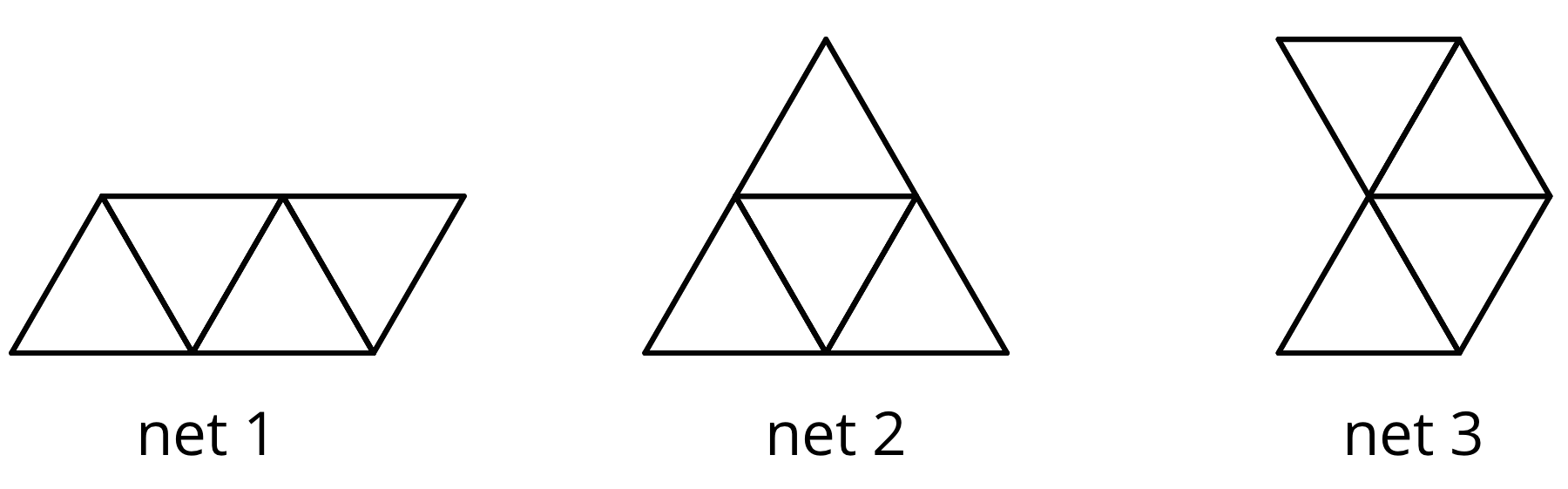A polyhedron is a three-dimensional figure composed of faces. Each face is a filled-in polygon and meets only one other face along a complete edge. The ends of the edges meet at points that are called vertices.
A polyhedron always encloses a three-dimensional region.
The plural of polyhedron is polyhedra. Here are some drawings of polyhedra:
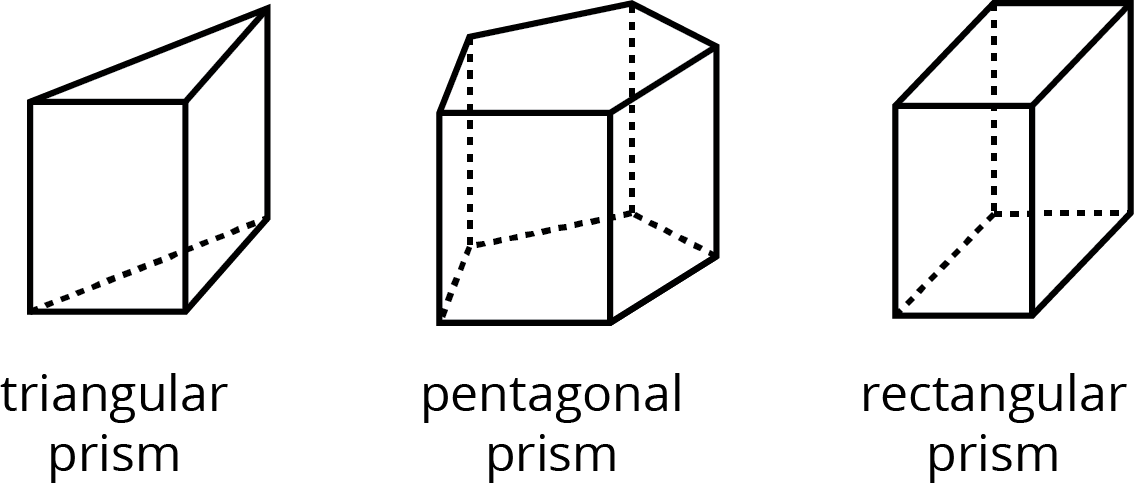
A prism is a type of polyhedron with two identical faces that are parallel to each other and that are called bases. The bases are connected by a set of rectangles (or sometimes parallelograms).
A prism is named for the shape of its bases. For example, if the base is a pentagon, then it is called a “pentagonal prism.”
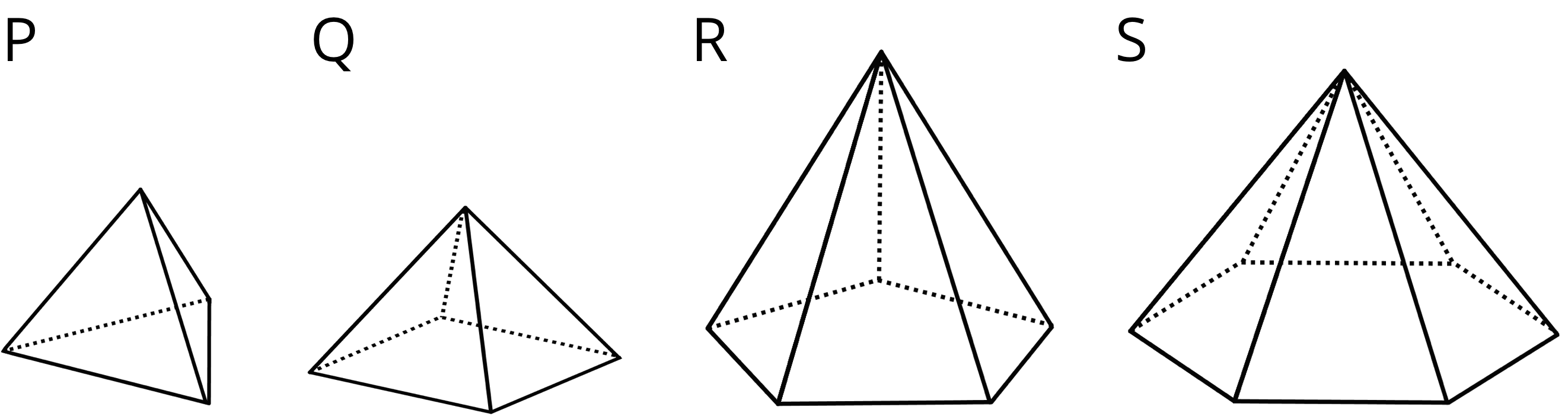
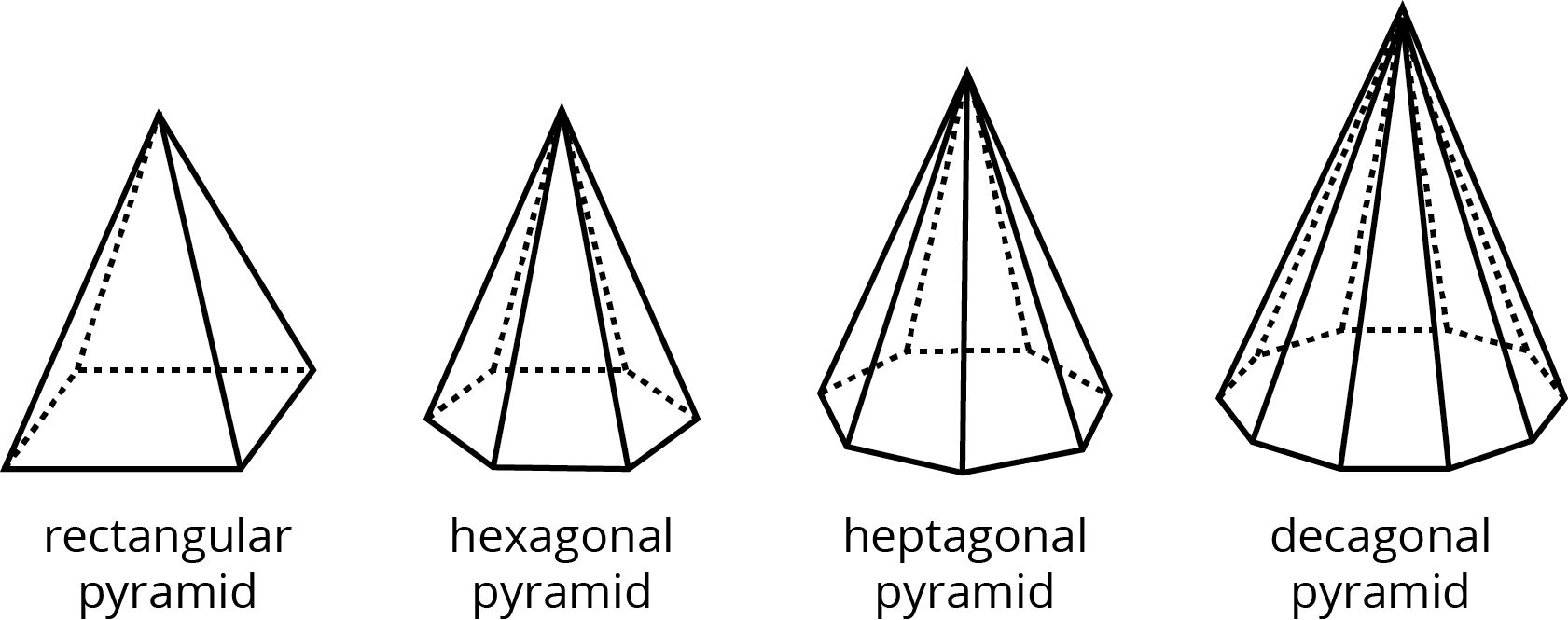
A pyramid is a type of polyhedron that has one special face called the base. All of the other faces are triangles that all meet at a single vertex.
A pyramid is named for the shape of its base. For example, if the base is a pentagon, then it is called a “pentagonal pyramid.”
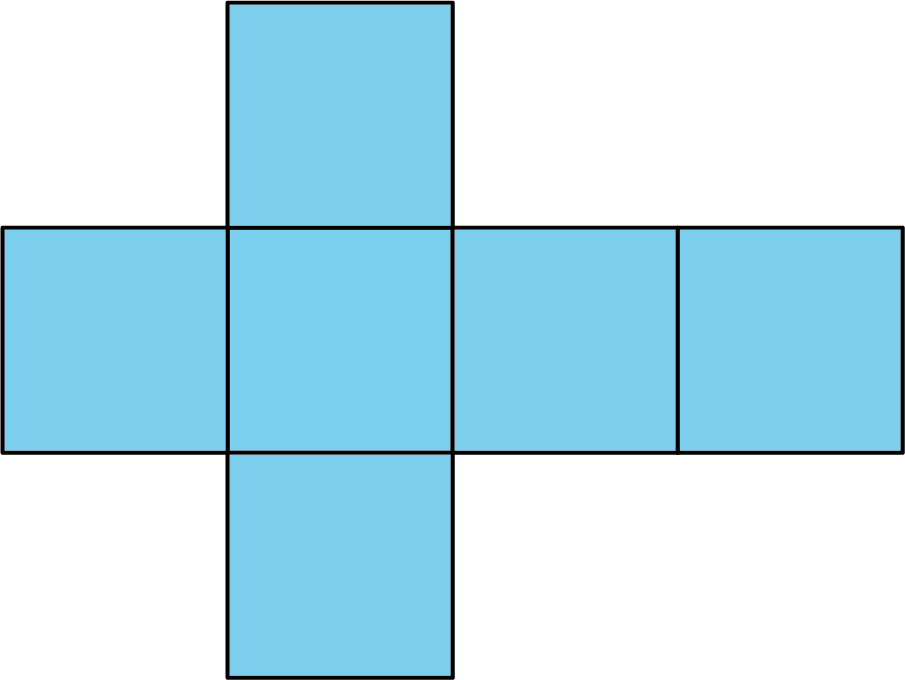
A net is a two-dimensional representation of a polyhedron. It is composed of polygons that form the faces of a polyhedron.
A cube has 6 square faces, so its net is composed of six squares, as shown here.
A net can be cut out and folded to make a model of the polyhedron.
In a cube, every face shares its edges with 4 other squares. In a net of a cube, not all edges of the squares are joined with another edge. When the net is folded, however, each of these open edges will join another edge.
It takes practice to visualize the final polyhedron by just looking at a net.