14.1: Matching Nets
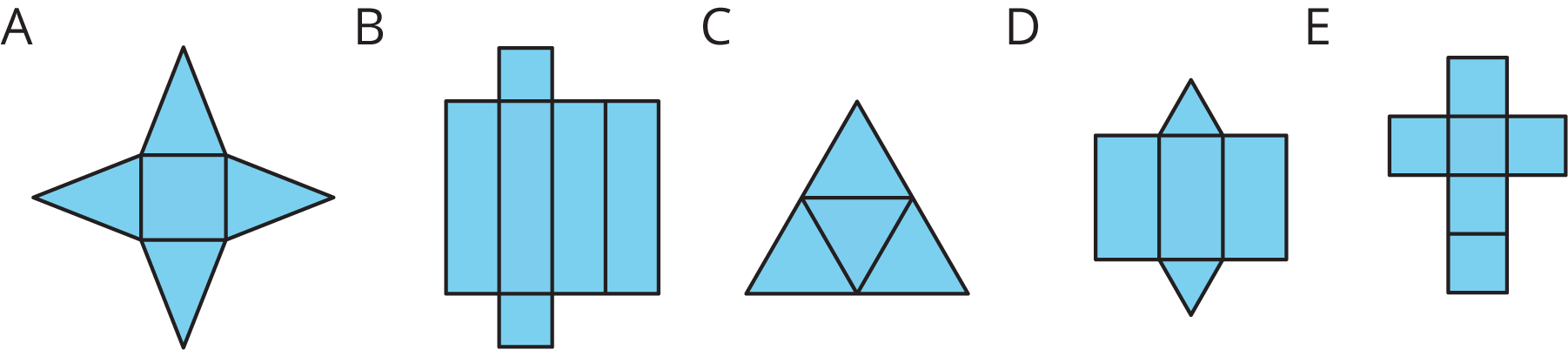
Each of the following nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.

Let’s use nets to find the surface area of polyhedra.
Each of the following nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.


Your teacher will give you the nets of three polyhedra to cut out and assemble.
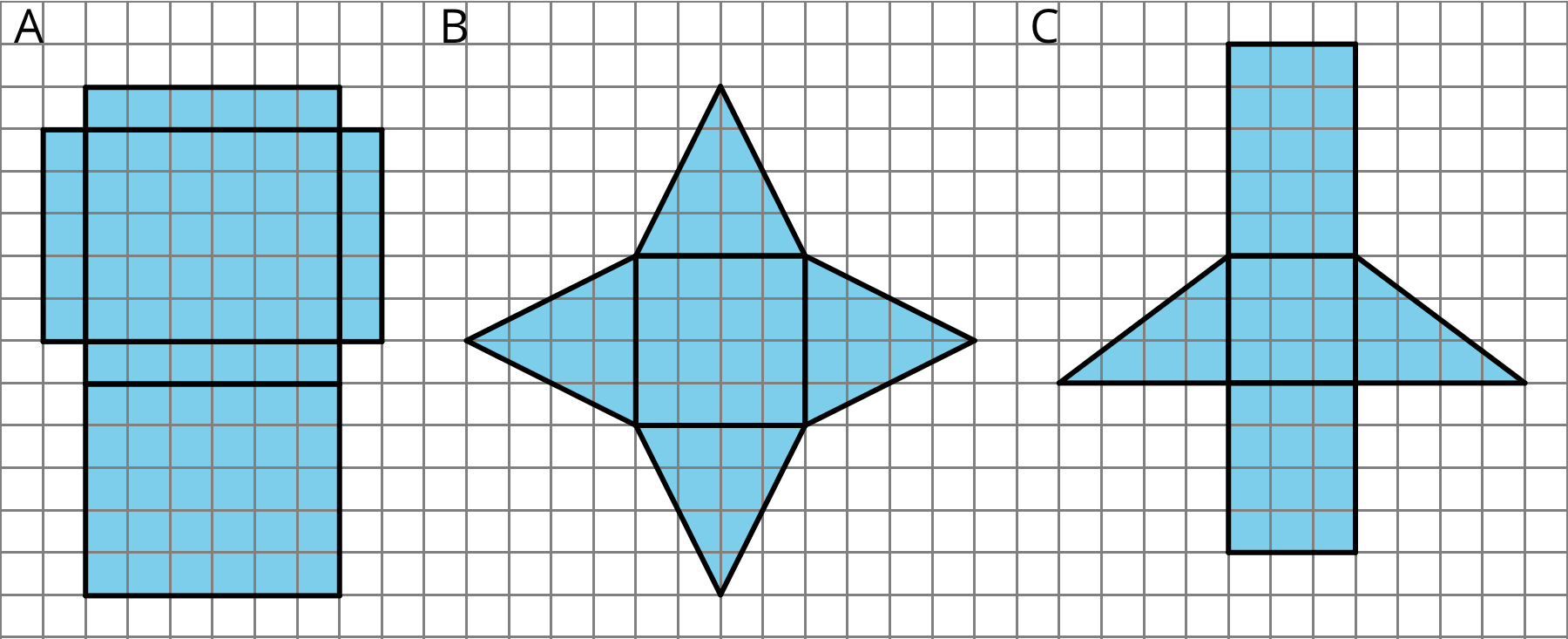
A:
B:
C:
Cut out your nets and use them to create three-dimensional shapes.
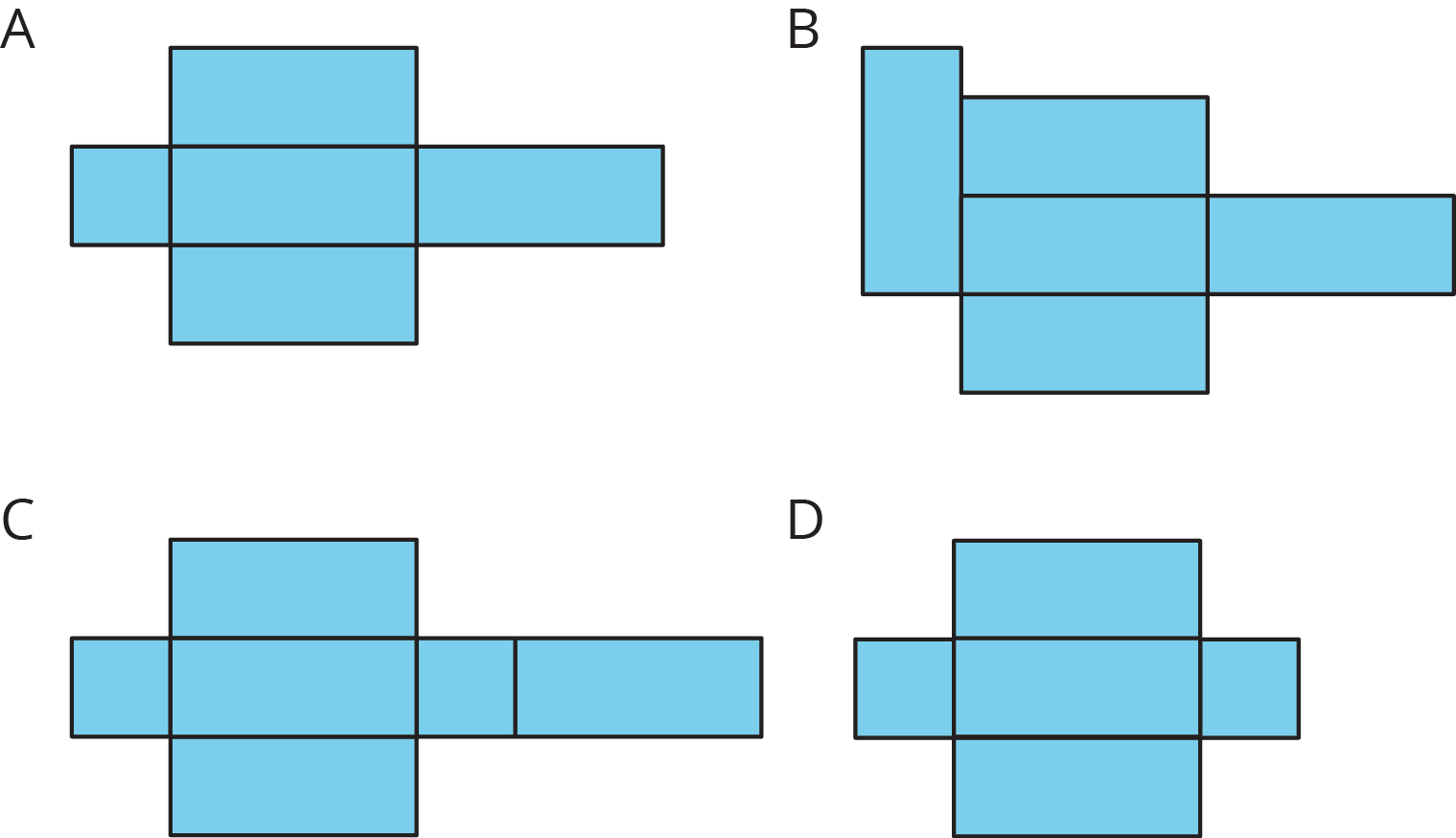
For each of these nets, decide if it can be assembled into a rectangular prism.
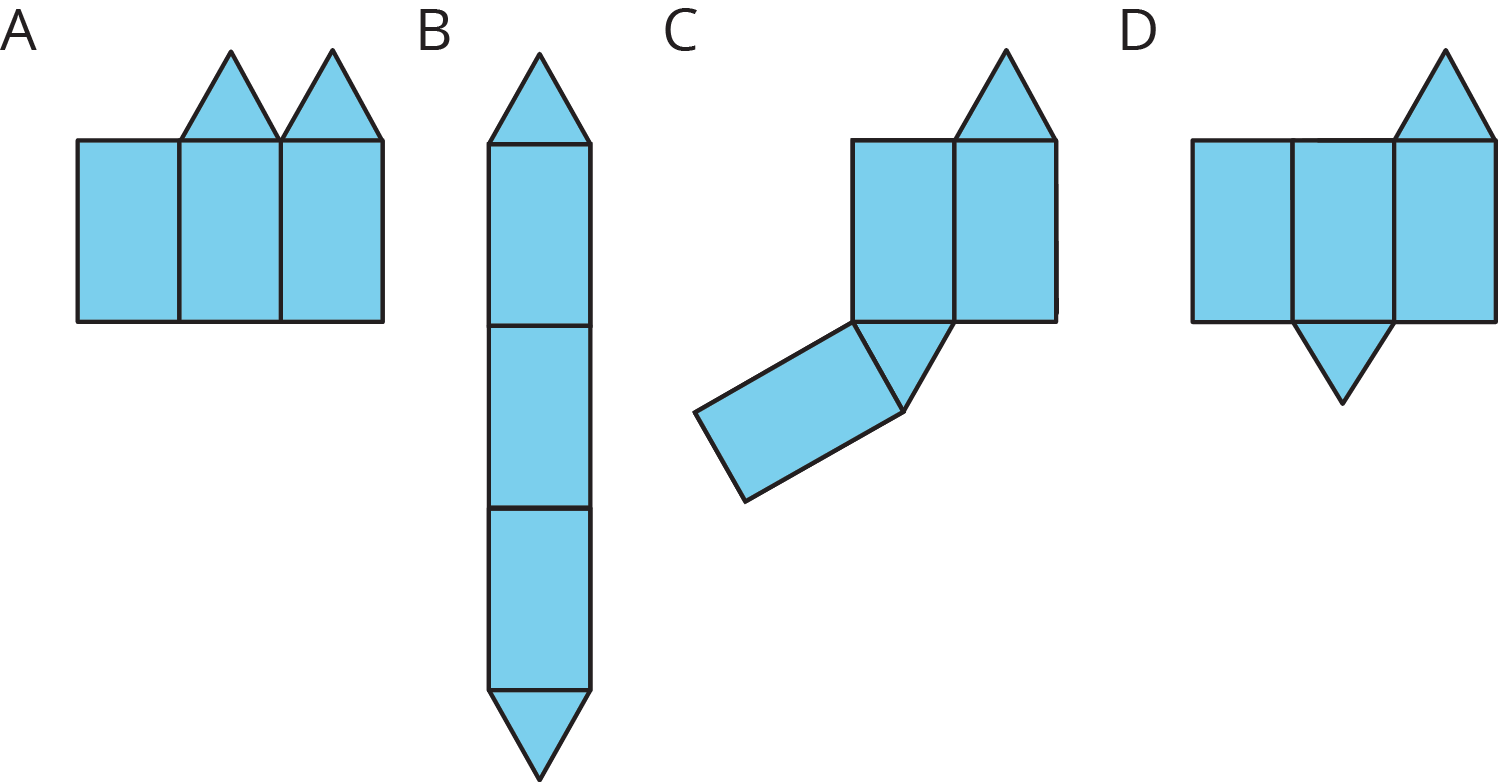
For each of these nets, decide if it can be folded into a triangular prism.
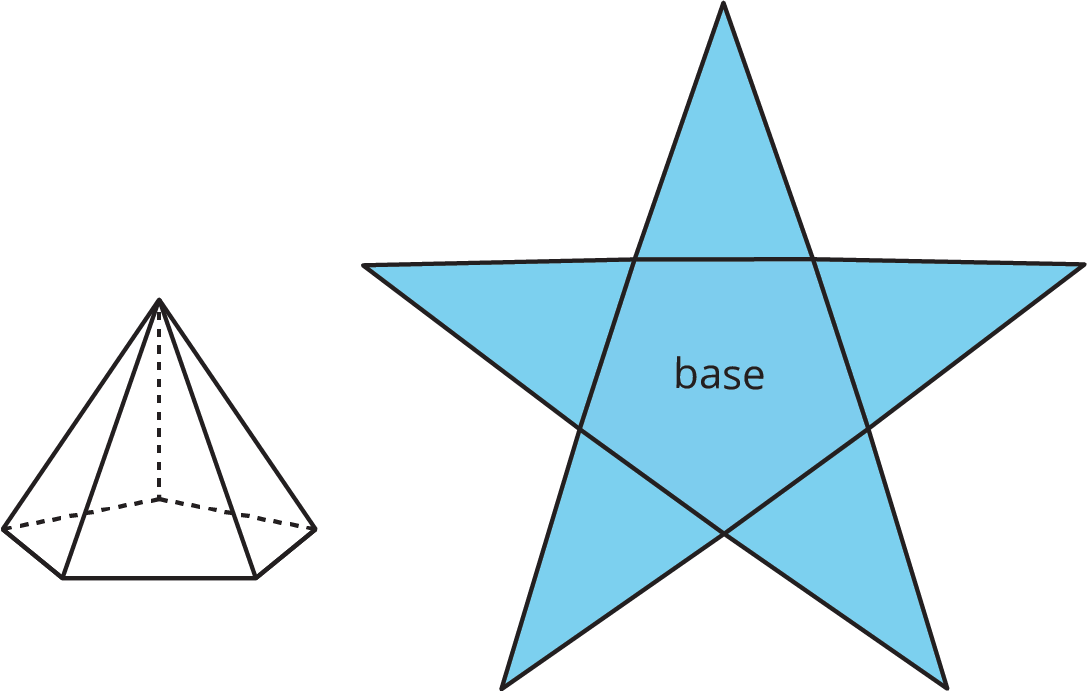
A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A pentagonal pyramid and its net are shown here.
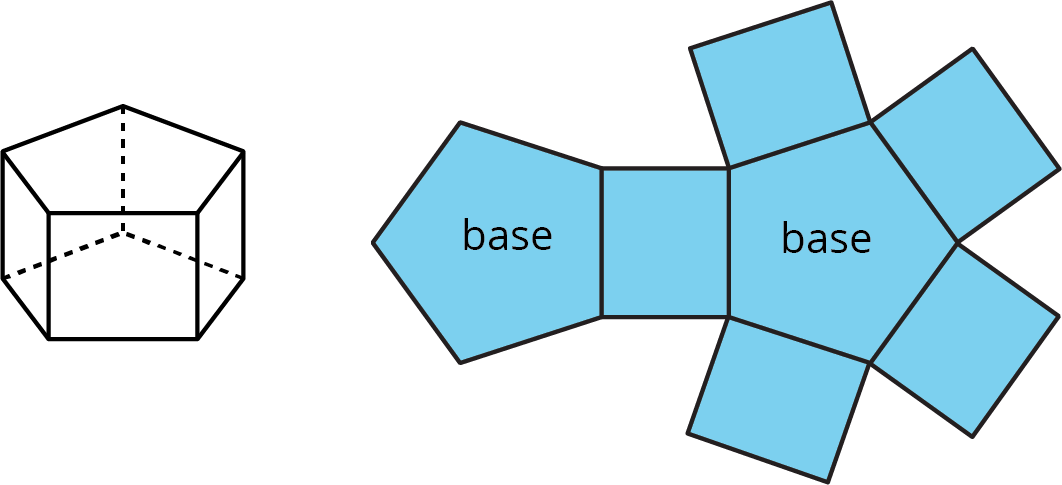
A net of a prism has two copies of the polygon that is the base. The rest of the polygons are rectangles. A pentagonal prism and its net are shown here.
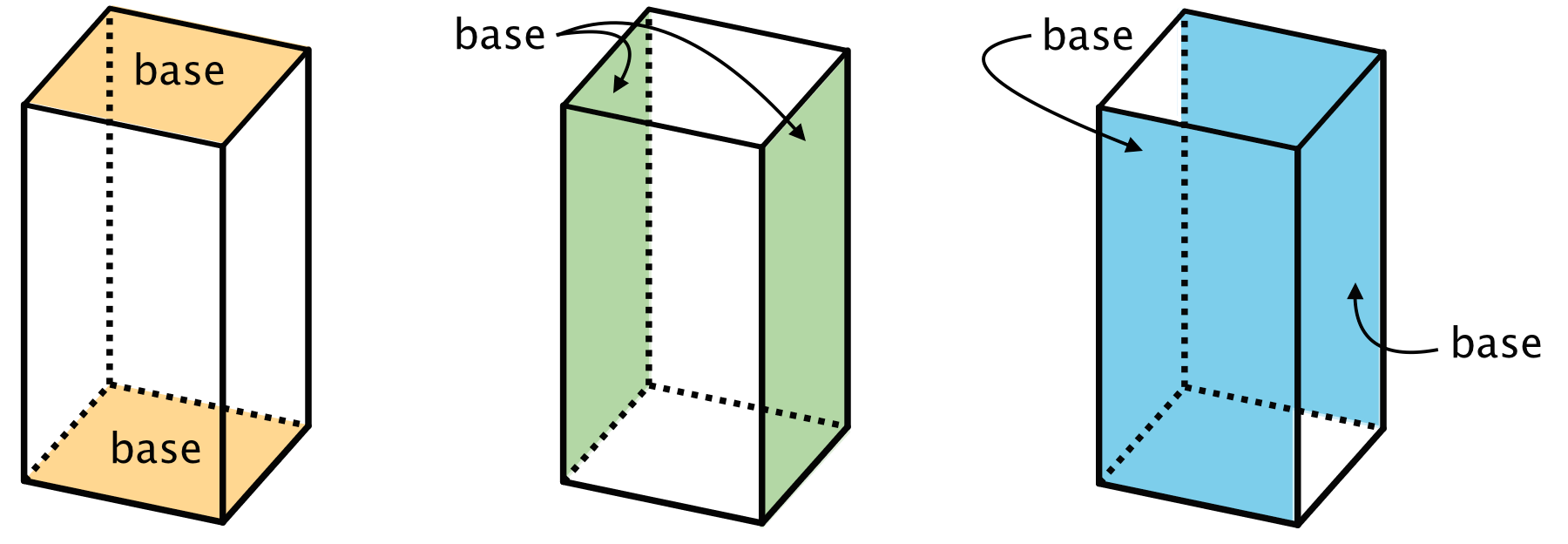
In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases.
For instance, the net of a rectangular prism shows three pairs of rectangles: 4 units by 2 units, 3 units by 2 units, and 4 units by 3 units.
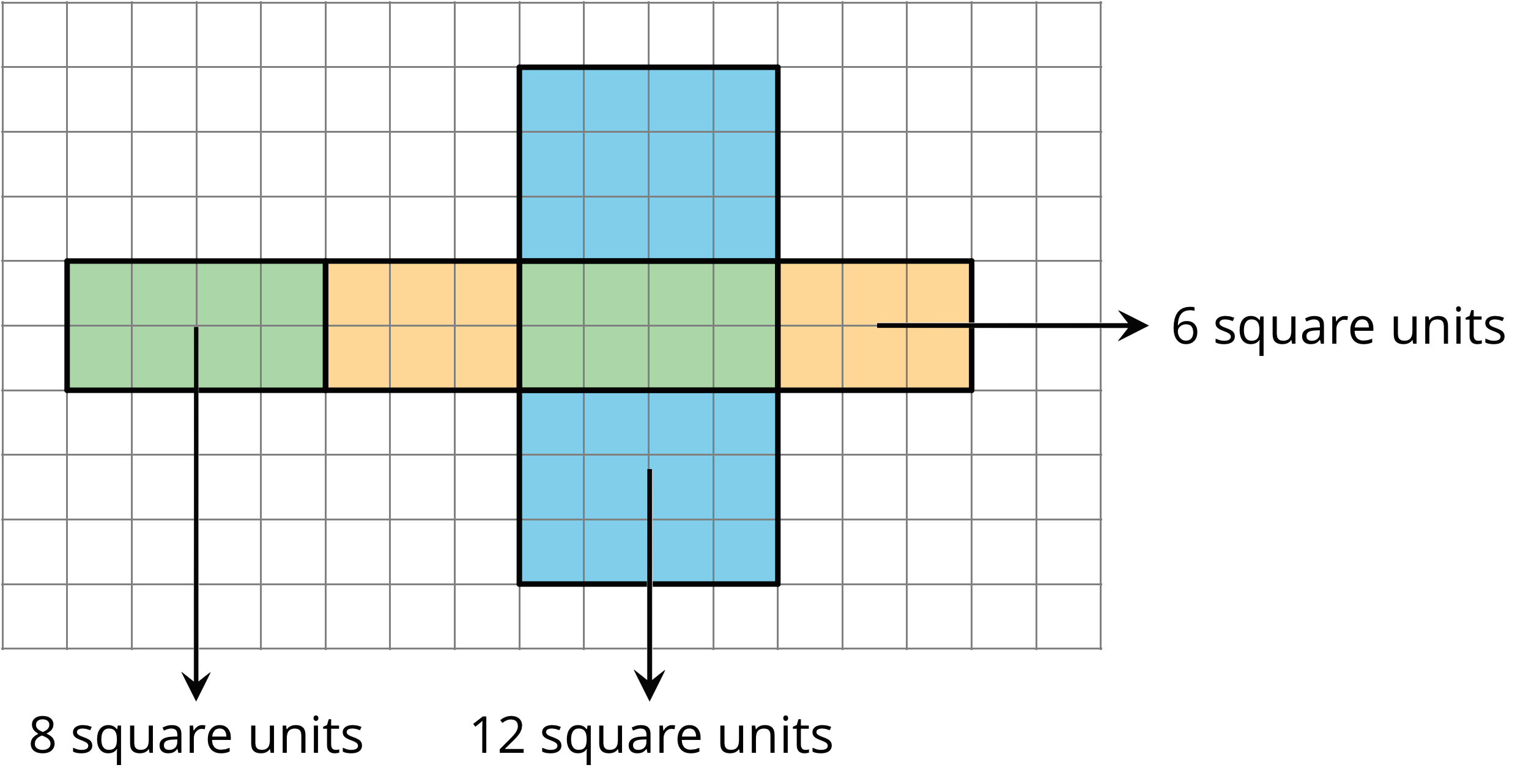
The surface area of the rectangular prism is 52 square units because $8+8+6+6+12+12=52$.