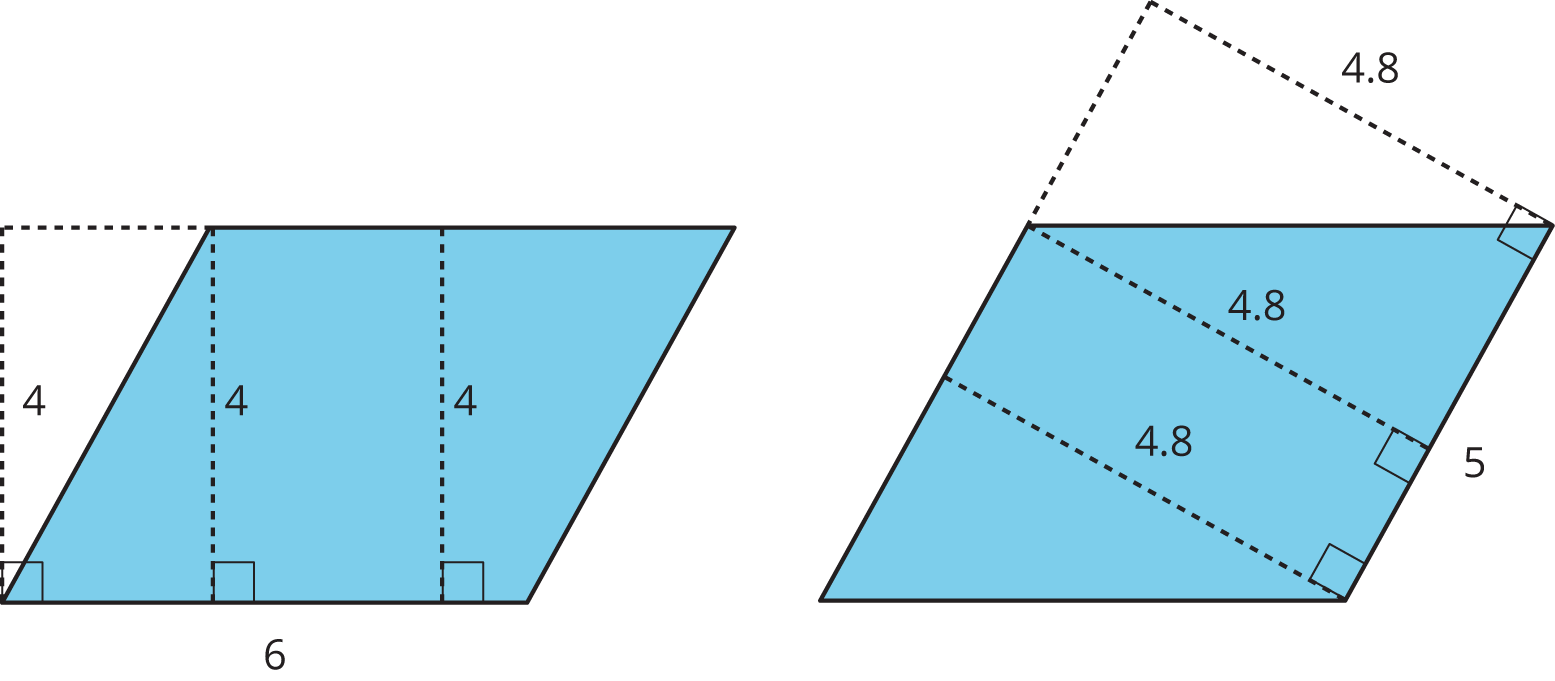
Here are two copies of the same parallelogram. On the left, the side that is the base is 6 units long. Its corresponding height is 4 units. On the right, the side that is the base is 5 units long. Its height is 4.8 units. For both, three different segments are shown to represent the height. We could draw in many more!
No matter which side is chosen as the base, the area of the parallelogram is the product of that base and its corresponding height. We can check it:
$$4 \times 6 = 24$$ and $$4.8 \times 5 = 24$$
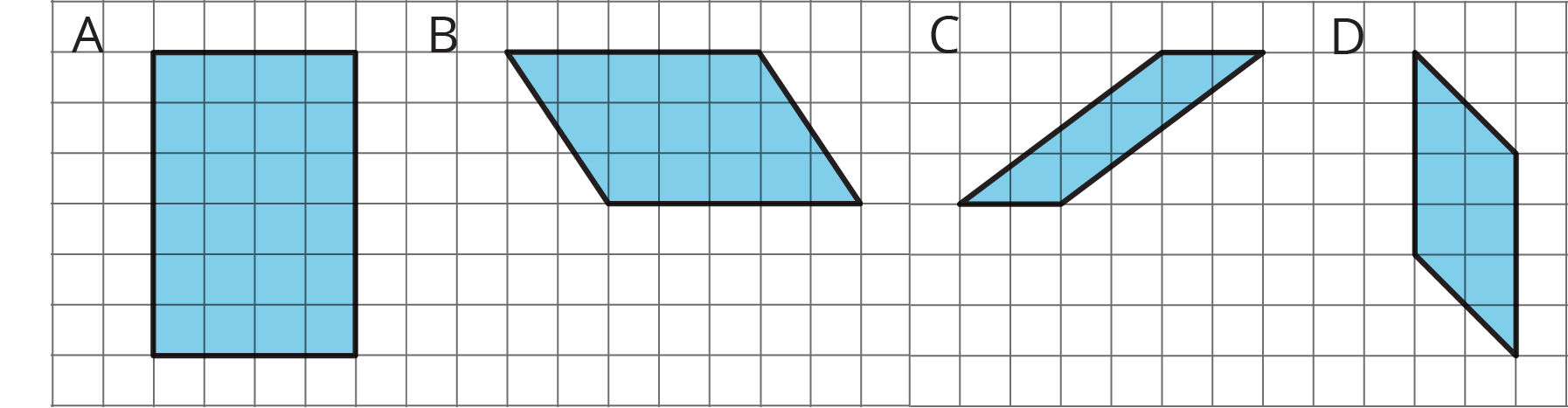
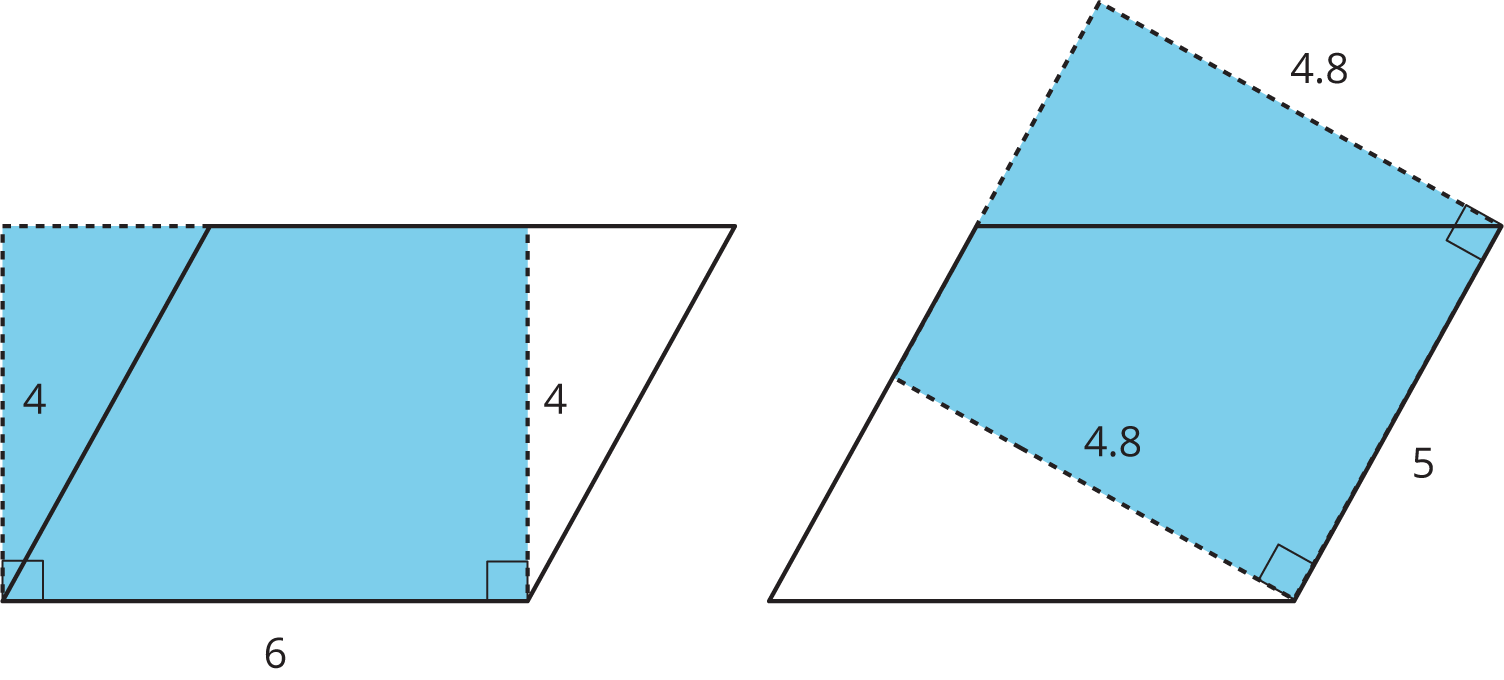
We can see why this is true by decomposing and rearranging the parallelograms into rectangles.
Notice that the side lengths of each rectangle are the base and height of the parallelogram. Even though the two rectangles have different side lengths, the products of the side lengths are equal, so they have the same area! And both rectangles have the same area as the parallelogram.
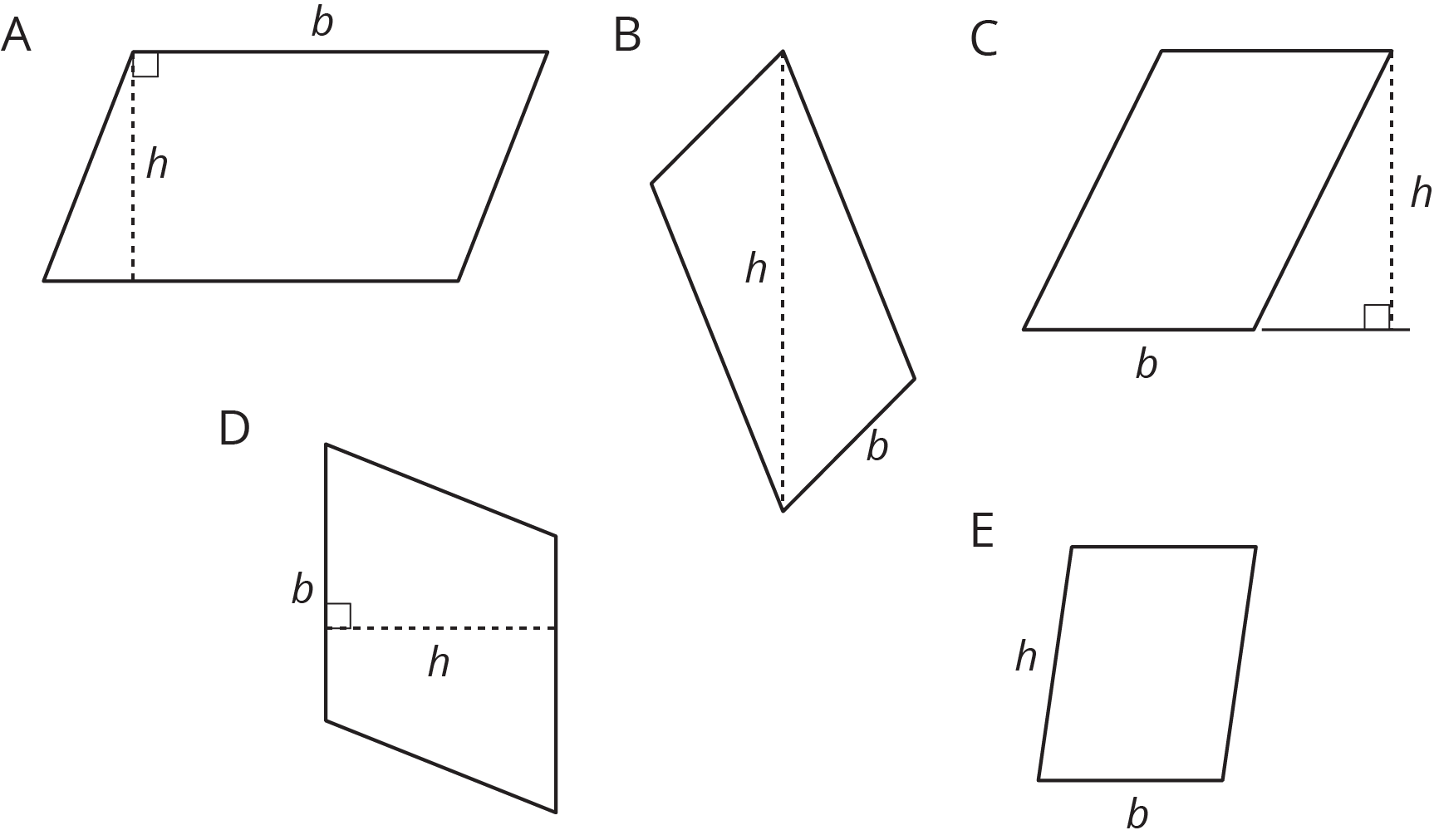
We often use letters to stand for numbers. If $b$ is base of a parallelogram (in units), and $h$ is the corresponding height (in units), then the area of the parallelogram (in square units) is the product of these two numbers. $$b \boldcdot h$$
Notice that we write the multiplication symbol with a small dot instead of a $\times$ symbol. This is so that we don’t get confused about whether $\times$ means multiply, or whether the letter $x$ is standing in for a number.
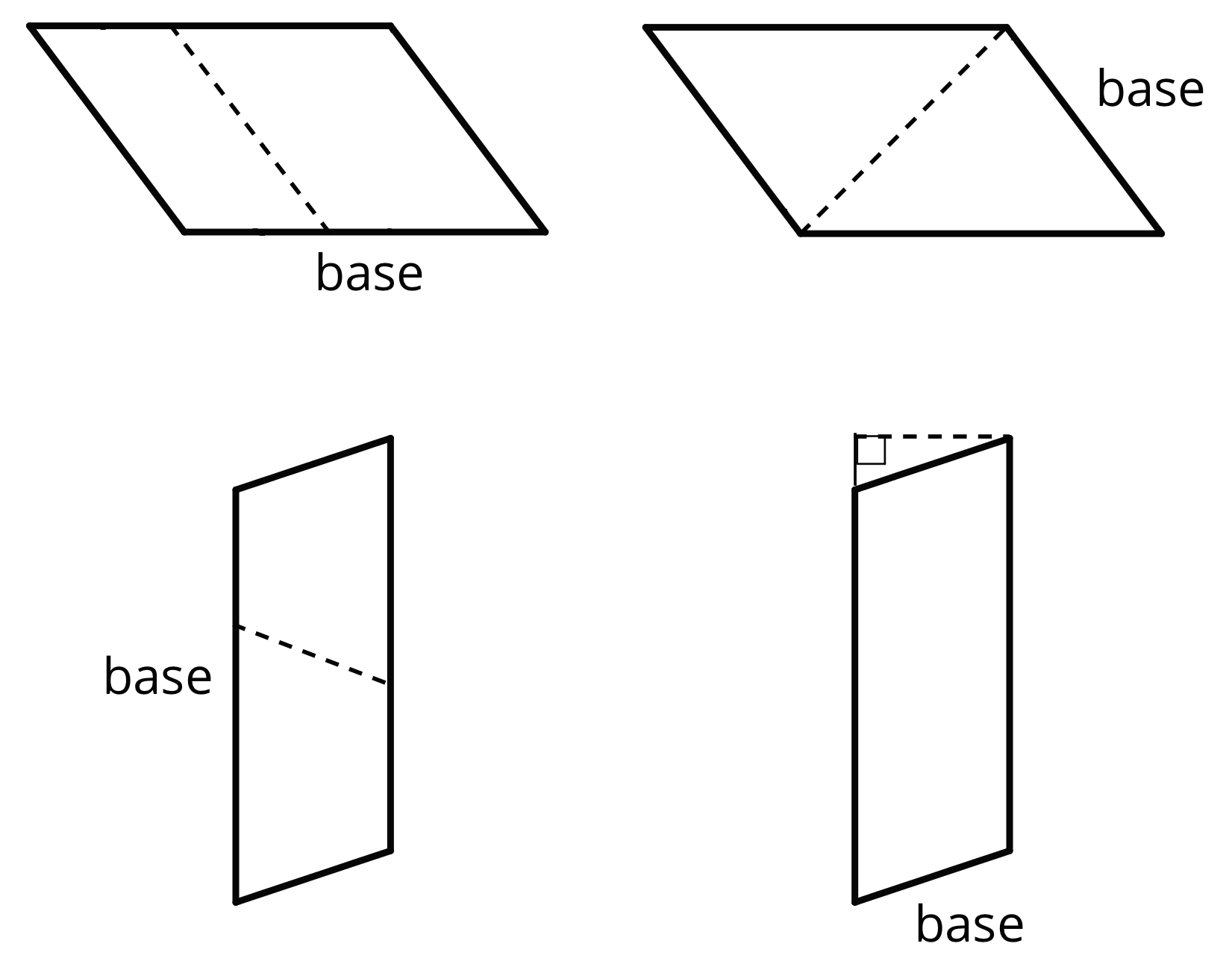
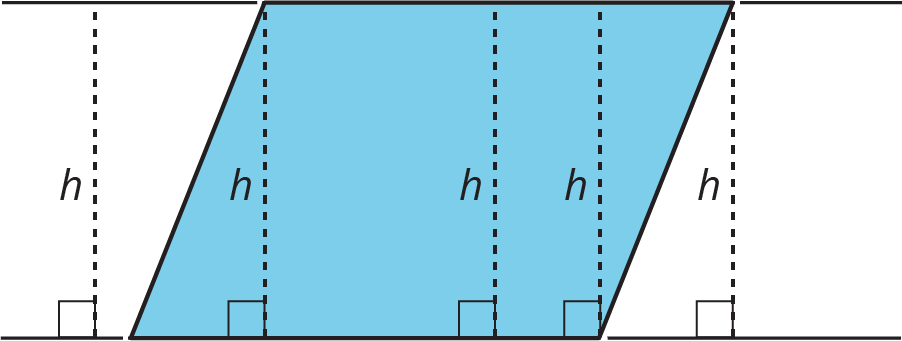
In high school, you will be able to prove that a perpendicular segment from a point on one side of a parallelogram to the opposite side will always have the same length.
You can see this most easily when you draw a parallelogram on graph paper. For now, we will just use this as a fact.