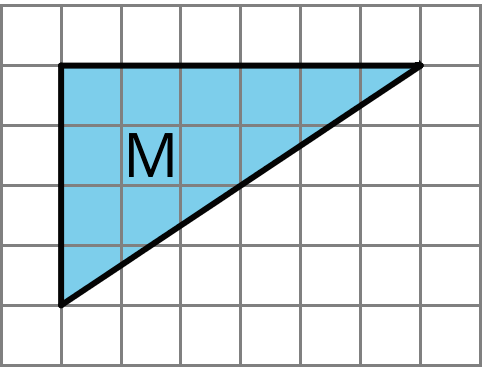
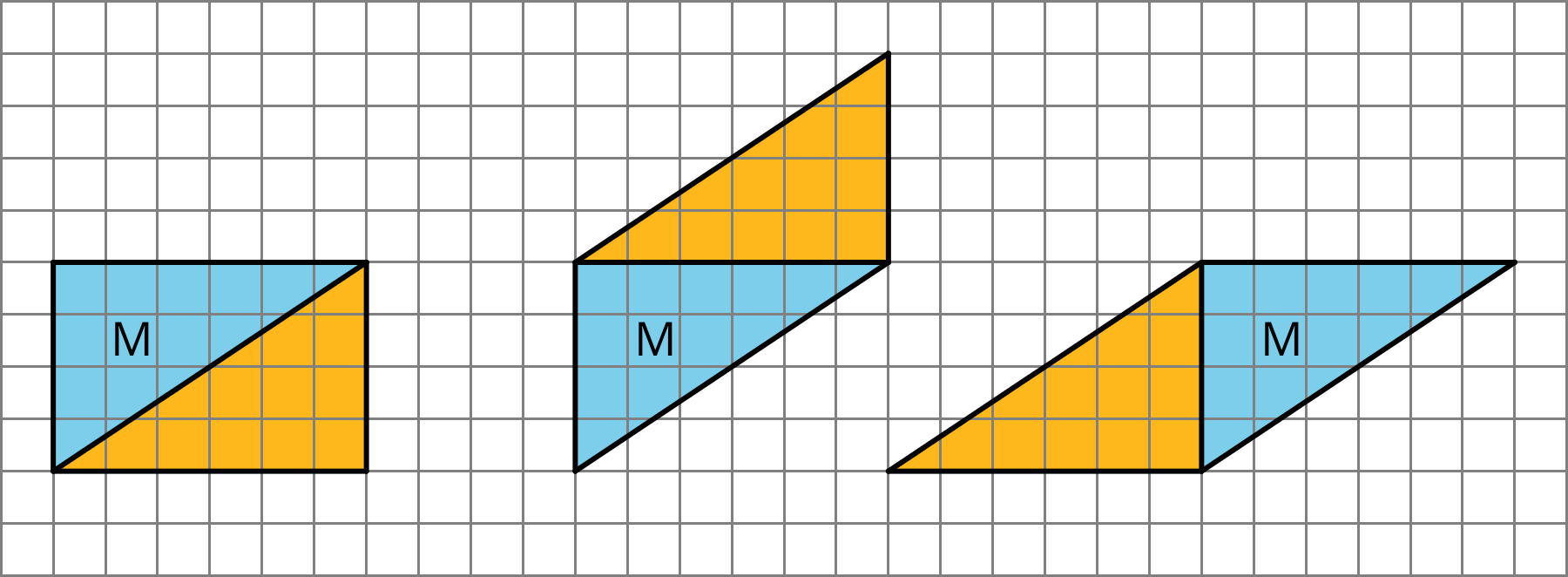
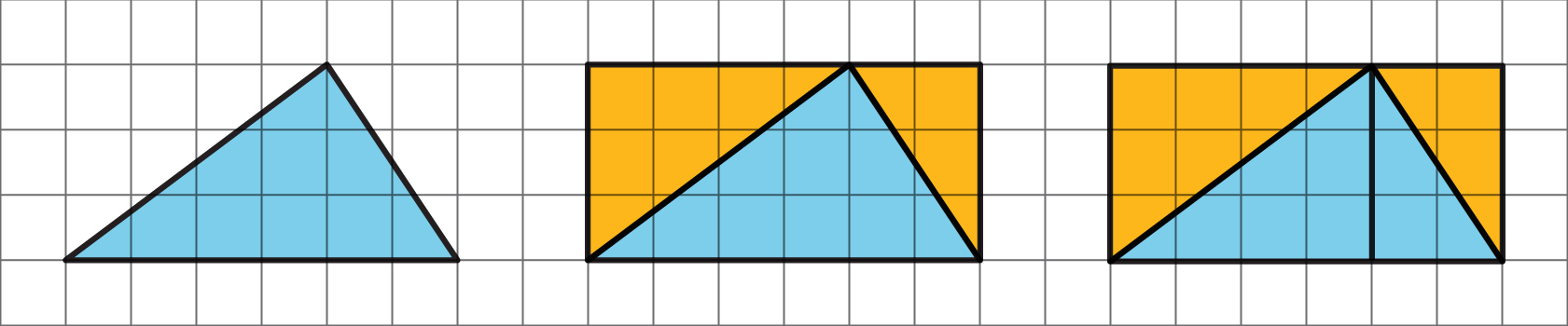
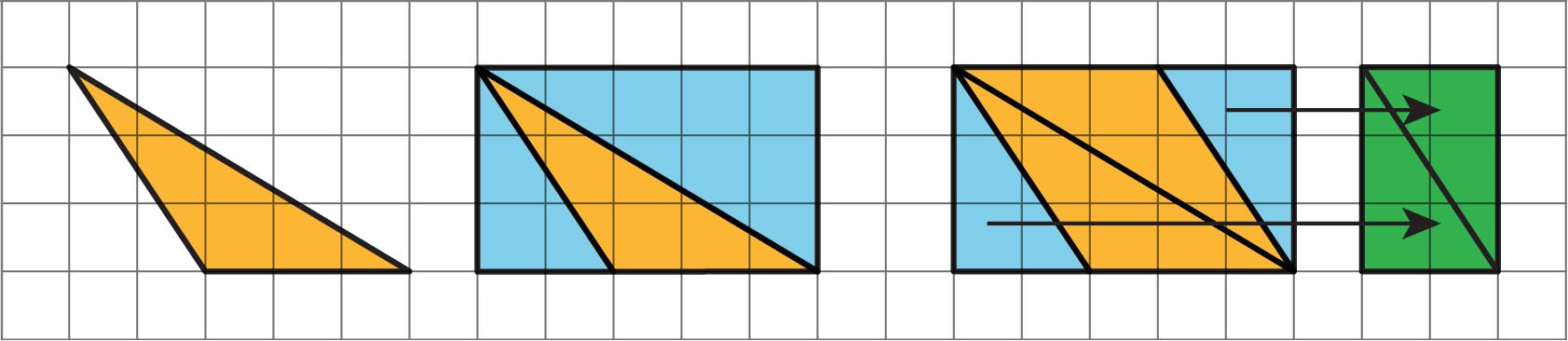
We can reason about the area of a triangle by using what we know about parallelograms. Here are three general ways to do this:
-
Make a copy of the triangle and join the original and the copy along an edge to create a parallelogram. Because the two triangles have the same area, one copy of the triangle has half the area of that parallelogram.
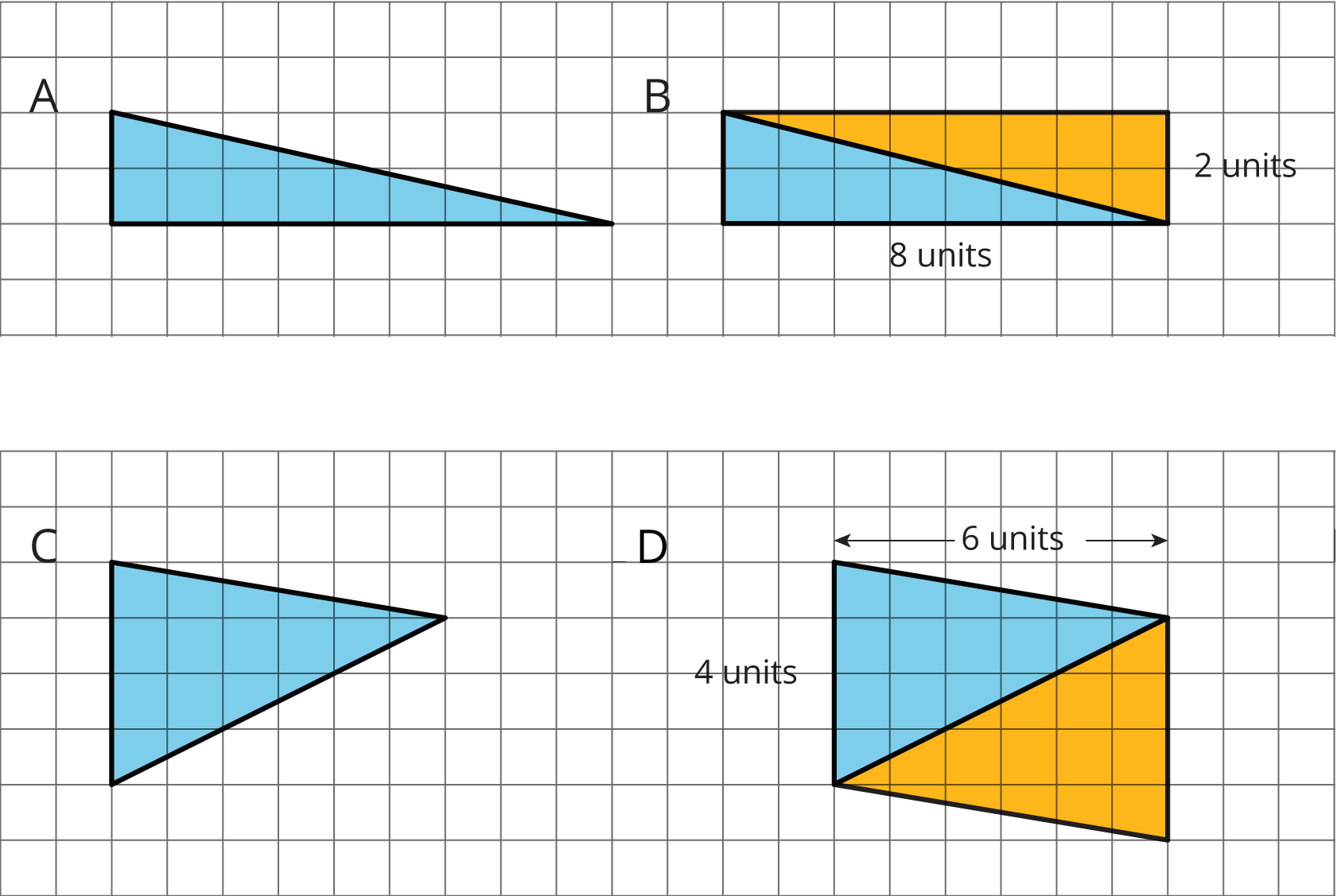
The area of Parallelogram B is 16 square units because the base is 8 units and the height 2 units. The area of Triangle A is half of that, which is 8 square units. The area of Parallelogram D is 24 square units because the base is 4 units and the height 6 units. The area of Triangle C is half of that, which is 12 square units.
-
Decompose the triangle into smaller pieces and compose them into a parallelogram.
In the new parallelogram, $b = 6$, $h = 2$, and $6 \boldcdot 2 = 12$, so its area is 12 square units. Because the original triangle and the parallelogram are composed of the same parts, the area of the original triangle is also 12 square units.
-
Draw a rectangle around the triangle. Sometimes the triangle has half of the area of the rectangle.
The large rectangle can be decomposed into smaller rectangles. The one on the left has area $4 \boldcdot 3$ or 12 square units; the one on the right has area $2 \boldcdot 3$ or 6 square units. The large triangle is also decomposed into two right triangles. Each of the right triangles is half of a smaller rectangle, so their areas are 6 square units and 3 square units. The large triangle has area 9 square units.
Sometimes, the triangle is half of what is left of the rectangle after removing two copies of the smaller right triangles.
The right triangles being removed can be composed into a small rectangle with area $(2 \boldcdot 3)$ square units. What is left is a parallelogram with area $5 \boldcdot 3 - 2 \boldcdot 3$, which equals $15-6$ or 9 square units. Notice that we can compose the same parallelogram with two copies of the original triangle! The original triangle is half of the parallelogram, so its area is $ \frac12 \boldcdot 9$ or 4.5 square units.