1.1: What Kind and How Many?
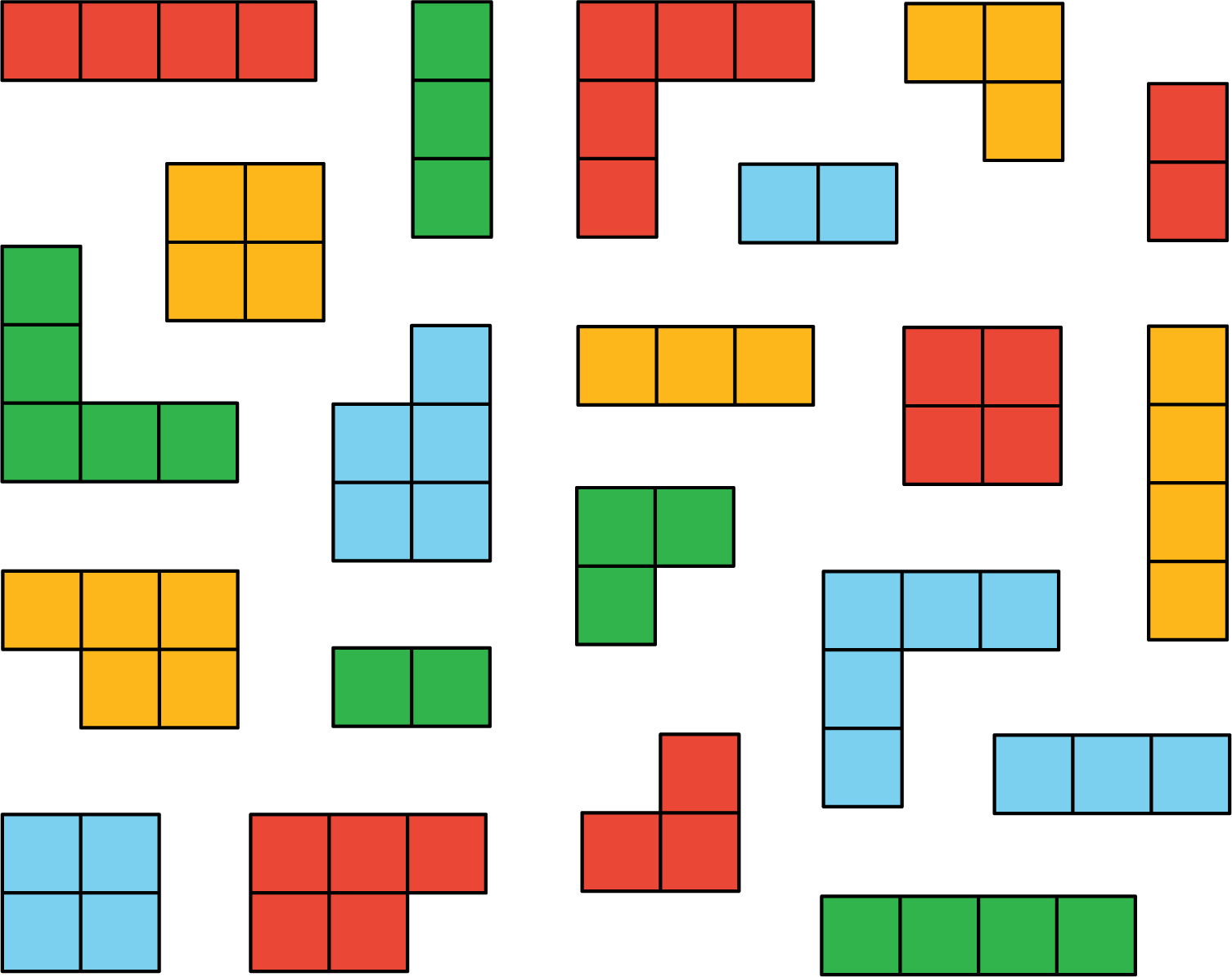
- If you sorted this set by color, how many groups would you have?
- If you sorted this set by area, how many groups would you have?
- Think of a third way you could sort these figures. What categories would you use? How many groups would you have?