Sometimes we want to know whether two situations are described by the same rate. To do that, we can write an equivalent ratio for one or both situations so that one part of their ratios has the same value. Then we can compare the other part of the ratios.
For example, do these two paint mixtures make the same shade of orange?
- Kiran mixes 9 teaspoons of red paint with 15 teaspoons of yellow paint.
- Tyler mixes 7 teaspoons of red paint with 10 teaspoons of yellow paint.
Here is a double number line that represents Kiran's paint mixture. The ratio $9:15$ is equivalent to the ratios $3:5$ and $6:10$.
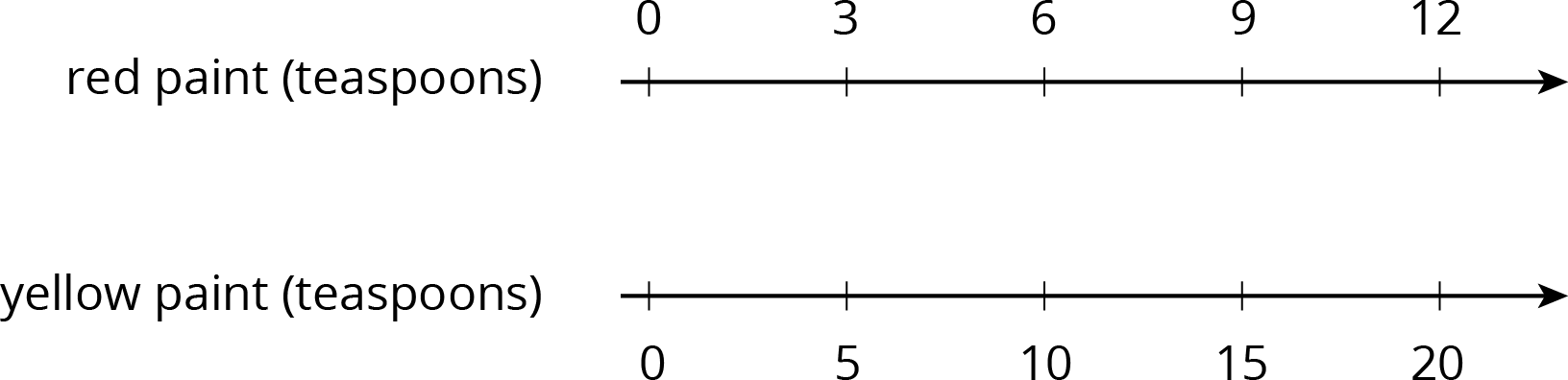
For 10 teaspoons of yellow paint, Kiran would mix in 6 teaspoons of red paint. This is less red paint than Tyler mixes with 10 teaspoons of yellow paint. The ratios $6:10$ and $7:10$ are not equivalent, so these two paint mixtures would not be the same shade of orange.
When we talk about two things happening at the same rate, we mean that the ratios of the quantities in the two situations are equivalent. There is also something specific about the situation that is the same.
- If two ladybugs are moving at the same rate, then they are traveling at the same constant speed.
- If two bags of apples are selling for the same rate, then they have the same unit price.
- If we mix two kinds of juice at the same rate, then the mixtures have the same taste.
- If we mix two colors of paint at the same rate, then the mixtures have the same shade.


