12.1: Number Talk: Multiplying by a Unit Fraction
Find the product mentally.
$\frac13\boldcdot 21$
$\frac16 \boldcdot 21$
$(5.6) \boldcdot \frac18$
$\frac14\boldcdot (5.6)$
Let’s use a table of equivalent ratios like a pro.
Find the product mentally.
$\frac13\boldcdot 21$
$\frac16 \boldcdot 21$
$(5.6) \boldcdot \frac18$
$\frac14\boldcdot (5.6)$
| number of tacos | price in dollars | |
|---|---|---|
| row 1 | ||
| row 2 | ||
| row 3 | ||
| row 4 | ||
| row 5 |
Use the table to help you solve these problems. Explain or show your reasoning.
Lin is paid \$90 for 5 hours of work. She used the following table to calculate how much she would be paid at this rate for 8 hours of work.
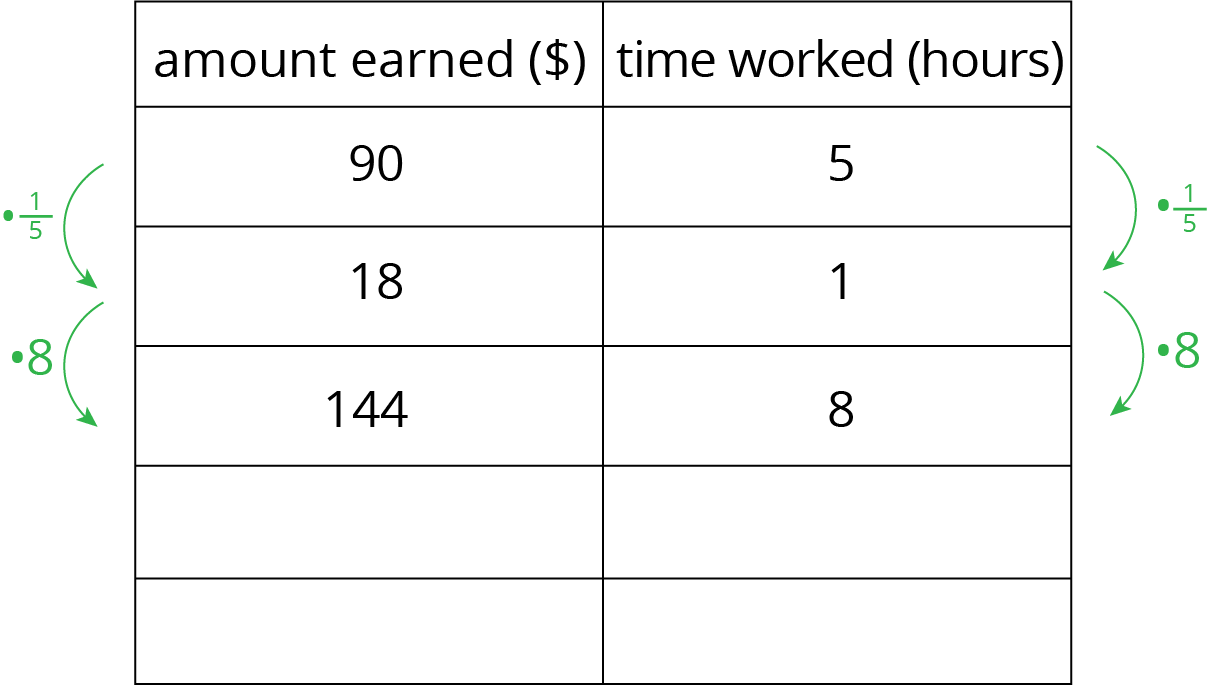
At this rate, how much would Lin be paid for 3 hours of work? For 2.1 hours of work?
In 2016, 128 gigabytes (GB) of portable computer memory cost \$32.
Here is a double number line that represents the situation:

One set of tick marks has already been drawn to show the result of multiplying 128 and 32 each by $\frac12$. Label the amount of memory and the cost for these tick marks.
Next, keep multiplying by $\frac12$ and drawing and labeling new tick marks, until you can no longer clearly label each new tick mark with a number.
Here is a table that represents the situation. Find the cost of 1 gigabyte. You can use as many rows as you need.
| memory (gigabytes) | cost (dollars) | |
|---|---|---|
| row 1 | 128 | 32 |
| row 2 | ||
| row 3 | ||
| row 4 | ||
| row 5 | ||
| row 6 | ||
| row 7 | ||
| row 8 |
A kilometer is 1,000 meters because kilo is a prefix that means 1,000. The prefix mega means 1,000,000 and giga (as in gigabyte) means 1,000,000,000. One byte is the amount of memory needed to store one letter of the alphabet. About how many of each of the following would fit on a 1-gigabyte flash drive?
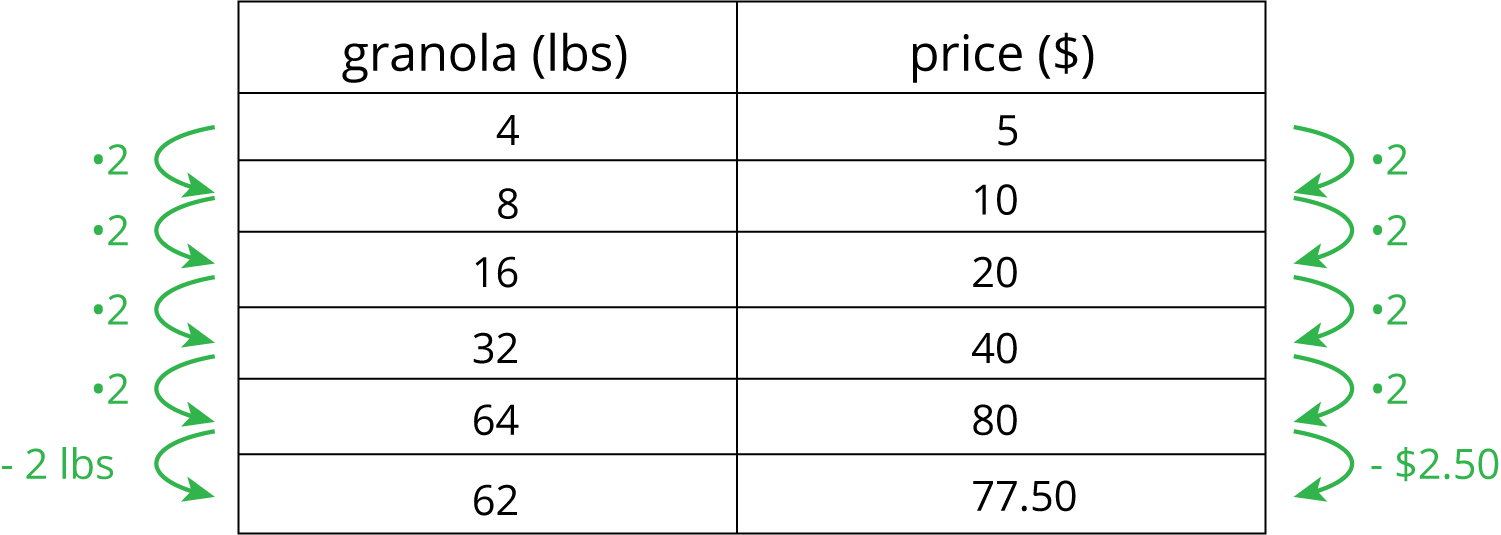
Finding a row containing a “1” is often a good way to work with tables of equivalent ratios. For example, the price for 4 lbs of granola is \$5. At that rate, what would be the price for 62 lbs of granola?
Here are tables showing two different approaches to solving this problem. Both of these approaches are correct. However, one approach is more efficient.
Less efficient
More efficient
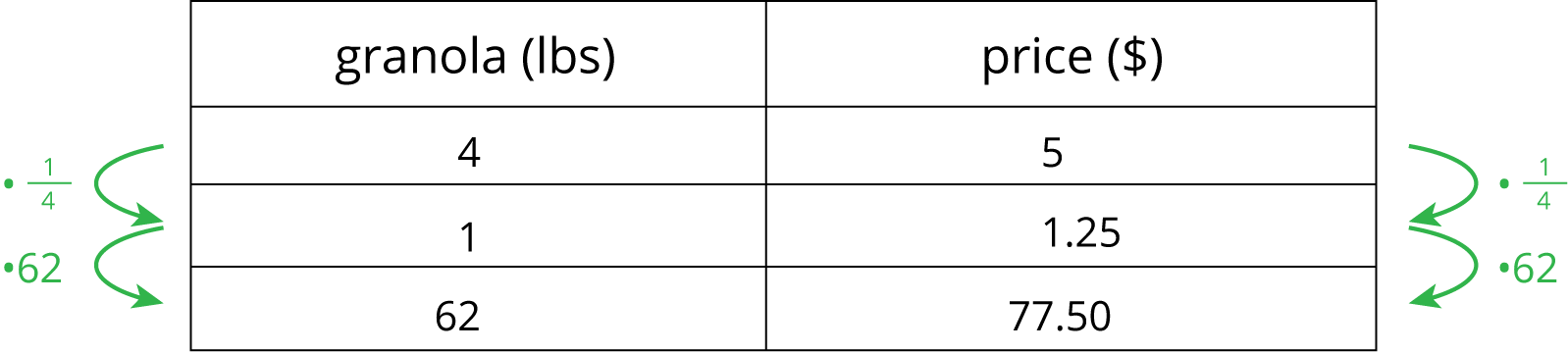
Notice how the more efficient approach starts by finding the price for 1 lb of granola.