6.1: Number Talk: Adjusting Another Factor
Find the value of each product mentally.
$(4.5)\boldcdot 4$
$(4.5)\boldcdot 8$
$\frac{1} {10}\boldcdot 65$
$\frac{2} {10}\boldcdot 65$
Let’s use number lines to represent equivalent ratios.
Find the value of each product mentally.
$(4.5)\boldcdot 4$
$(4.5)\boldcdot 8$
$\frac{1} {10}\boldcdot 65$
$\frac{2} {10}\boldcdot 65$
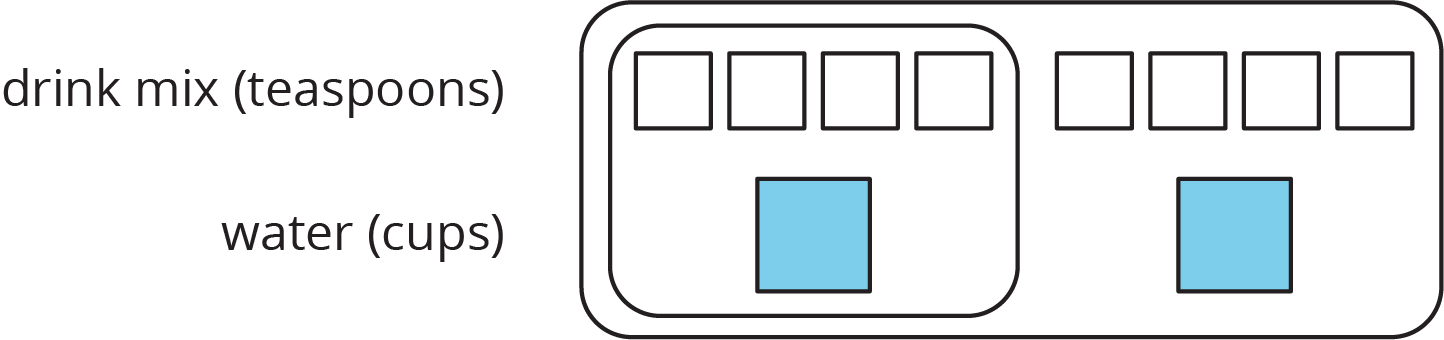
The other day, we made drink mixtures by mixing 4 teaspoons of powdered drink mix for every cup of water. Here are two ways to represent multiple batches of this recipe:
Recall that a perfect square is a number of objects that can be arranged into a square. For example, 9 is a perfect square because 9 objects can be arranged into 3 rows of 3. 16 is also a perfect square, because 16 objects can be arranged into 4 rows of 4. In contrast, 12 is not a perfect square because you can’t arrange 12 objects into a square.
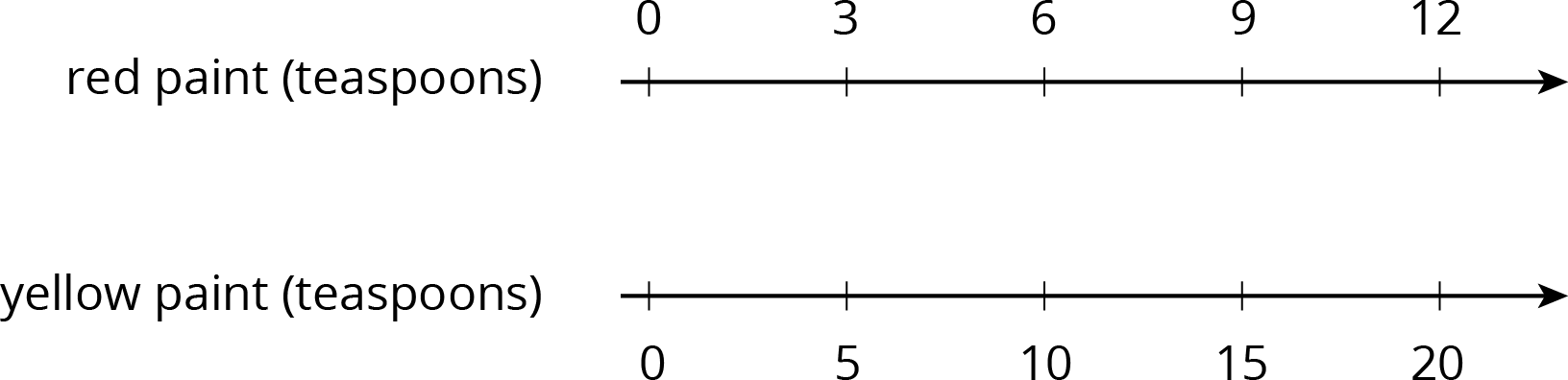
Here is a diagram showing Elena’s recipe for light blue paint.

Complete the double number line diagram to show the amounts of white paint and blue paint in different-sized batches of light blue paint.
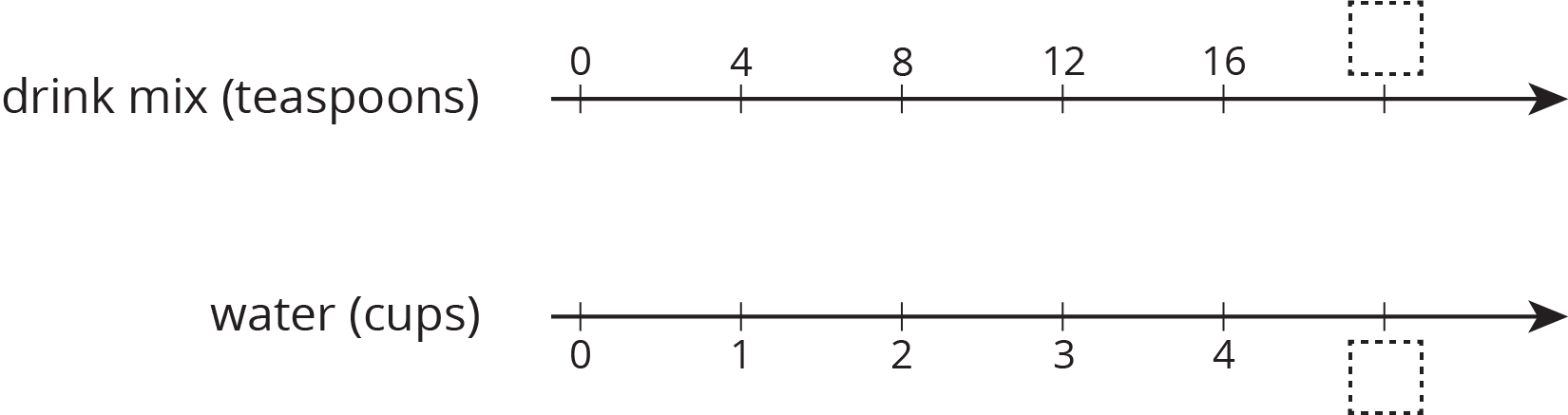
You can use a double number line diagram to find many equivalent ratios. For example, a recipe for fizzy juice says, “Mix 5 cups of cranberry juice with 2 cups of soda water.” The ratio of cranberry juice to soda water is $5:2$. Multiplying both ingredients by the same number creates equivalent ratios.
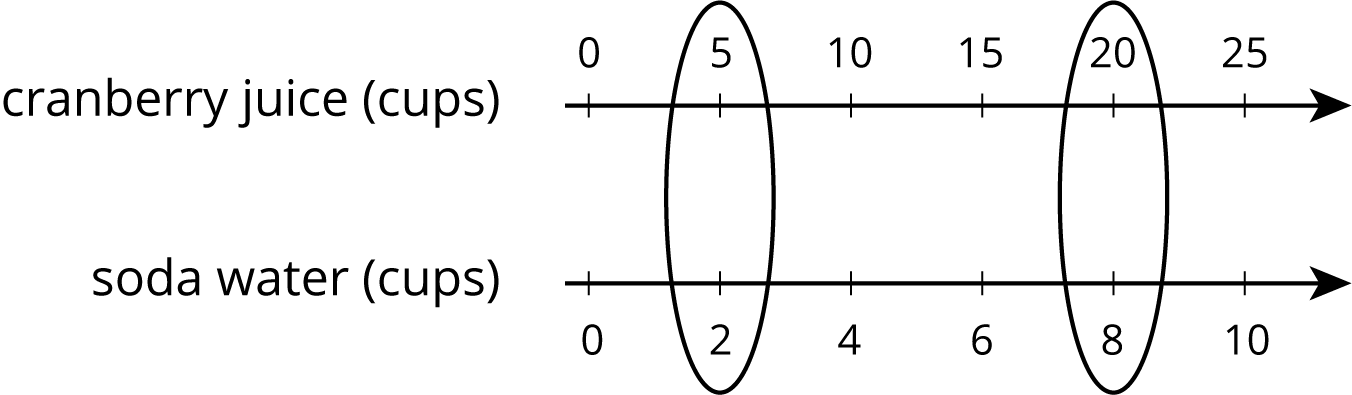
This double number line shows that the ratio $20:8$ is equivalent to $5:2$. If you mix 20 cups of cranberry juice with 8 cups of soda water, it makes 4 times as much fizzy juice that tastes the same as the original recipe.
A double number line diagram is a pair of parallel number lines with the numbers 0 aligned. Each number line is marked in equal increments and numbered. The tick marks are aligned, but the numbers on the two lines are often different. A pair of aligned numbers on the diagram represents a ratio that is equivalent to every other pair of aligned numbers on the diagram.