7.1: Ordering on a Number Line
-
Locate and label the following numbers on the number line:
$\frac12$
$\frac14$
$1\frac34$
1.5
1.75
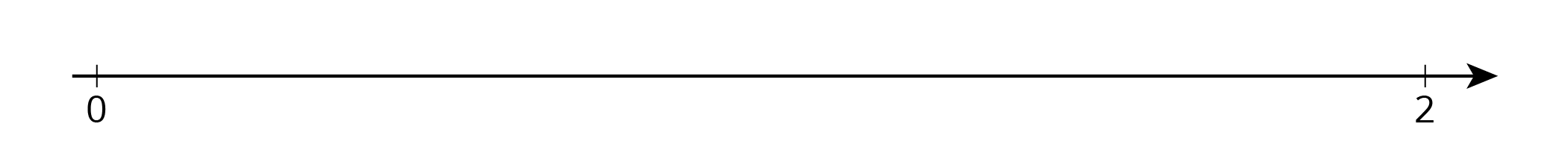
- Based on where you placed the numbers, locate and label four more fractions or decimals on the number line.
Let's draw double number line diagrams like a pro.
Locate and label the following numbers on the number line:
$\frac12$
$\frac14$
$1\frac34$
1.5
1.75
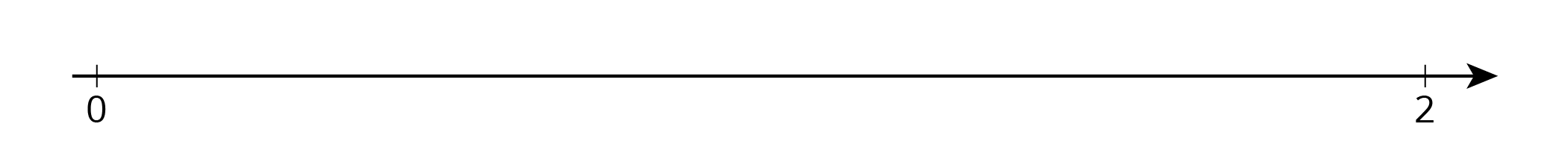
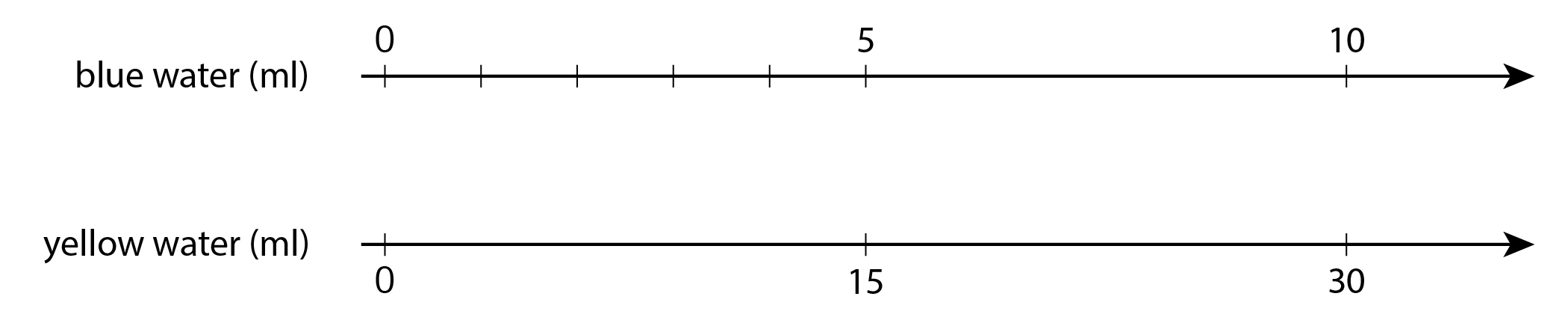
The other day, we made green water by mixing 5 ml of blue water with 15 ml of yellow water. We want to make a very small batch of the same shade of green water. We need to know how much yellow water to mix with only 1 ml of blue water.
A recipe for art paste says “For every 2 pints of water, mix in 8 cups of flour.”
Follow the instructions to draw a double number line diagram representing the recipe for art paste.
Compare your double number line diagram with your partner’s. Discuss your thinking. If needed, revise your diagram.
Next, use your double number line to answer these questions:
A square with side of 10 units overlaps a square with side of 8 units in such a way that its corner $B$ is placed exactly at the center of the smaller square. As a result of the overlapping, the two sides of the large square intersect the two sides of the small square exactly at points $C$ and $E$, as shown. The length of $CD$ is 6 units.

What is the area of the overlapping region $CDEB$?
The other day, we looked at a recipe for tuna casserole that called for 10 ounces of cream of chicken soup for every 3 cups of elbow-shaped pasta.
Here are some guidelines to keep in mind when drawing a double number line diagram:
For example, the ratio of the number of eggs to cups of milk in a recipe is $4:1$. Here is a double number line that represents the situation:
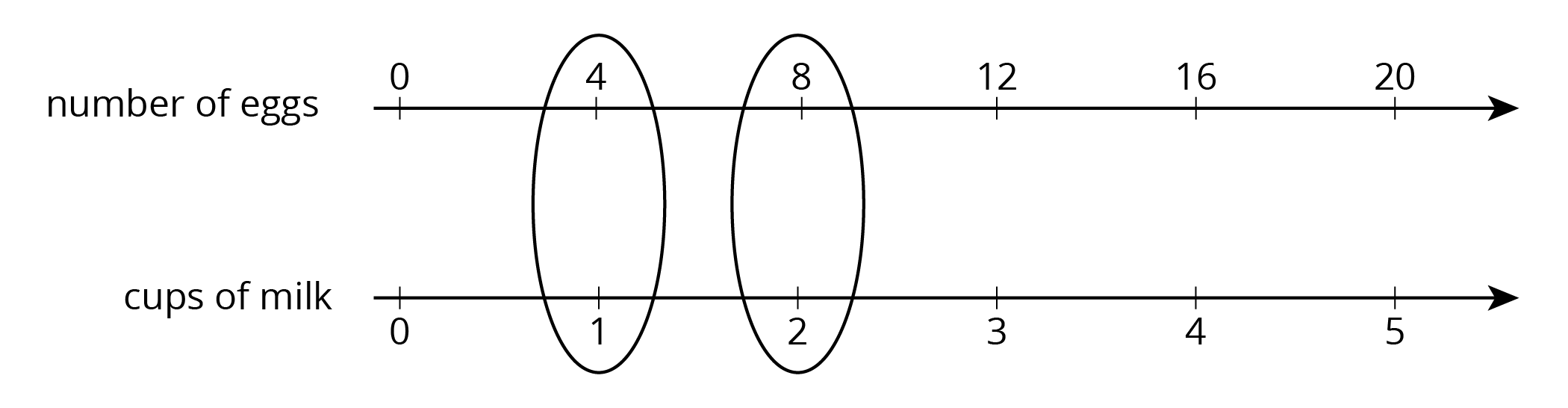
We can also say that this recipe uses “4 eggs per cup of milk” because the word per means “for each.”
The word per means “for each.” For example: he paid \$5 for each ticket, so the cost was \$5 per ticket.