
Unit 2: Practice Problem Sets
Lesson 1
Problem 1
In a fruit basket there are 9 bananas, 4 apples, and 3 plums.
- The ratio of bananas to apples is ________ : ________.
- The ratio of plums to apples is ________ to ________.
- For every ________ apples, there are ________ plums.
-
For every 3 bananas there is one ________.
Problem 2
Complete the sentences to describe this picture.

- The ratio of dogs to cats is _______.
- For every _____ dogs, there are _____ cats.
Problem 3
Write two different sentences that use ratios to describe the number of eyes and legs in this picture.

Problem 4 (from Unit 1, Lesson 17)
Choose an appropriate unit of measurement for each quantity.
- area of a rectangle
- volume of a prism
- side of a square
- area of a square
- volume of a cube
- cm
- cm3
- cm2
Problem 5 (from Unit 1, Lesson 16)
Find the volume and surface area of each prism.
- Prism A: 3 cm by 3 cm by 3 cm

- Prism B: 5 cm by 5 cm by 1 cm

-
Compare the volumes of the prisms and then their surface areas. Does the prism with the greater volume also have the greater surface area?
Problem 6 (from Unit 1, Lesson 13)
Which figure is a triangular prism? Select all that apply.

Lesson 2
Problem 1
Here is a diagram that describes the cups of green and white paint in a mixture.

Select all the statements that accurately describe this diagram.
- The ratio of cups of white paint to cups of green paint is 2 to 4.
- For every cup of green paint, there are two cups of white paint.
- The ratio of cups of green paint to cups of white paint is $4:2$.
- For every cup of white paint, there are two cups of green paint.
- The ratio of cups of green paint to cups of white paint is $2:4$.
Problem 2
To make a snack mix, combine 2 cups of raisins with 4 cups of pretzels and 6 cups of almonds.
- Create a diagram to represent the quantities of each ingredient in this recipe.
-
Use your diagram to complete each sentence.
- The ratio of __________________ to __________________ to __________________ is ________ : ________ : ________.
- There are ________ cups of pretzels for every cup of raisins.
- There are ________ cups of almonds for every cup of raisins.
Problem 3 (from Unit 1, Lesson 17)
- A square is 3 inches by 3 inches. What is its area?
- A square has a side length of 5 feet. What is its area?
- The area of a square is 36 square centimeters. What is the length of each side of the square?
Problem 4 (from Unit 1, Lesson 11)
Find the area of this quadrilateral. Explain or show your strategy.

Problem 5 (from Unit 2, Lesson 1)
Complete each equation with a number that makes it true.
- $\frac18 \boldcdot 8 = \text{_______}$
- $\frac38 \boldcdot 8 = \text{_______}$
- $\frac18 \boldcdot 7 = \text{_______}$
- $\frac38 \boldcdot 7 = \text{_______}$
Lesson 3
Problem 1
A recipe for 1 batch of spice mix says, “Combine 3 teaspoons of mustard seeds, 5 teaspoons of chili powder, and 1 teaspoon of salt.” How many batches are represented by the diagram? Explain or show your reasoning.

Problem 2
Priya makes chocolate milk by mixing 2 cups of milk and 5 tablespoons of cocoa powder. Draw a diagram that clearly represents two batches of her chocolate milk.
Problem 3
In a recipe for fizzy grape juice, the ratio of cups of sparkling water to cups of grape juice concentrate is 3 to 1.
- Find two more ratios of cups of sparkling water to cups of juice concentrate that would make a mixture that tastes the same as this recipe.
- Describe another mixture of sparkling water and grape juice that would taste different than this recipe.
Problem 4 (from Unit 2, Lesson 1)
Write the missing number under each tick mark on the number line.
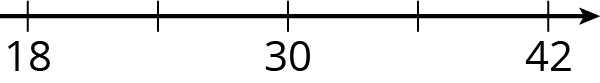
Problem 5 (from Unit 2, Lesson 1)
At the kennel, there are 6 dogs for every 5 cats.
- The ratio of dogs to cats is ______ to ______.
- The ratio of cats to dogs is ______ to ______.
- For every ______ dogs there are ______ cats.
- The ratio of cats to dogs is ______ : ______.
Problem 6 (from Unit 1, Lesson 17)
Elena has 80 unit cubes. What is the volume of the largest cube she can build with them?
Problem 7 (from Unit 2, Lesson 1)
Fill in the blanks to make each equation true.
- $3 \boldcdot \frac13 = \text{_______}$
- $10 \boldcdot \frac{1}{10} = \text{_______}$
- $19 \boldcdot \frac{1}{19} = \text{_______}$
- $a \boldcdot \frac{1}{a}= \text{_______}$
(As long as $a$ does not equal 0.)
- $5 \boldcdot \text{_______} = 1$
- $17 \boldcdot \text{_______} = 1$
- $b \boldcdot \text{_______} = 1$
Lesson 4
Problem 1
Here is a diagram showing a mixture of red paint and green paint needed for 1 batch of a particular shade of brown.
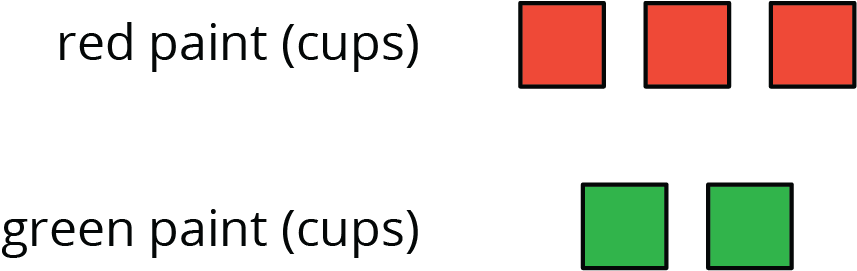
Add to the diagram so that it shows 3 batches of the same shade of brown paint.
Problem 2
Diego makes green paint by mixing 10 tablespoons of yellow paint and 2 tablespoons of blue paint. Which of these mixtures produce the same shade of green paint as Diego’s mixture? Select all that apply.
- For every 5 tablespoons of blue paint, mix in 1 tablespoon of yellow paint.
- Mix tablespoons of blue paint and yellow paint in the ratio $1:5$.
- Mix tablespoons of yellow paint and blue paint in the ratio 15 to 3.
- Mix 11 tablespoons of yellow paint and 3 tablespoons of blue paint.
Problem 3
To make 1 batch of sky blue paint, Clare mixes 2 cups of blue paint with 1 gallon of white paint.
- Explain how Clare can make 2 batches of sky blue paint.
- Explain how to make a mixture that is a darker shade of blue than the sky blue.
- Explain how to make a mixture that is a lighter shade of blue than the sky blue.
Problem 4 (from Unit 2, Lesson 2)
A smoothie recipe calls for 3 cups of milk, 2 frozen bananas and 1 tablespoon of chocolate syrup.
- Create a diagram to represent the quantities of each ingredient in the recipe.
- Write 3 different sentences that use a ratio to describe the recipe.
Problem 5 (from Unit 2, Lesson 1)
Write the missing number under each tick mark on the number line.
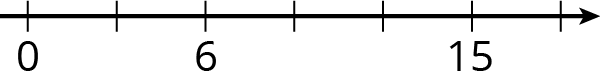
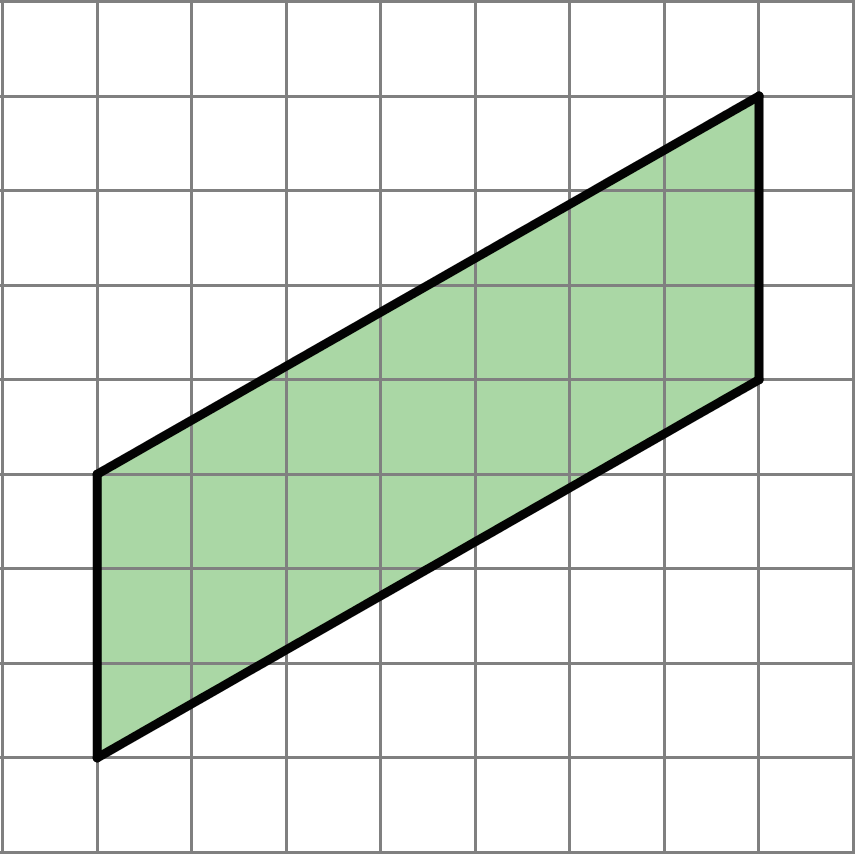
Problem 6 (from Unit 1, Lesson 4)
Find the area of the parallelogram. Show your reasoning.
Problem 7 (from Unit 2, Lesson 1)
Complete each equation with a number that makes it true.
- $11 \boldcdot \frac14= \text{_______}$
- $7 \boldcdot \frac14= \text{_______}$
- $13 \boldcdot \frac{1}{27}= \text{_______}$
- $13 \boldcdot \frac{1}{99}= \text{_______}$
- $x \boldcdot \frac{1}{y}= \text{_______}$
(As long as $y$ does not equal 0.)
Lesson 5
Problem 1
Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a diagram that shows why they are equivalent ratios.
- $4:5$ and $8:10$
- $18:3$ and $6:1$
- $2:7$ and $10,\!000:35,\!000$
Problem 2
Explain why $6:4$ and $18:8$ are not equivalent ratios.
Problem 3
Are the ratios $3:6$ and $6:3$ equivalent? Why or why not?
Problem 4 (from Unit 2, Lesson 4)
This diagram represents 3 batches of light yellow paint. Draw a diagram that represents 1 batch of the same shade of light yellow paint.

Problem 5 (from Unit 2, Lesson 1)
In the fruit bowl there are 6 bananas, 4 apples, and 3 oranges.
- For every 4 __________________, there are 3 __________________.
- The ratio of __________________ to __________________ is $6:3$.
- The ratio of __________________ to __________________ is 4 to 6.
- For every 1 orange, there are ______ bananas.
Problem 6 (from Unit 2, Lesson 1)
Write fractions for points $A$ and $B$ on the number line.
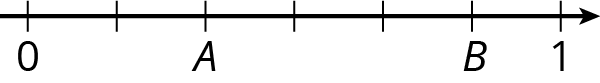
Lesson 6
Problem 1
A particular shade of orange paint has 2 cups of yellow paint for every 3 cups of red paint. On the double number line, circle the numbers of cups of yellow and red paint needed for 3 batches of orange paint.
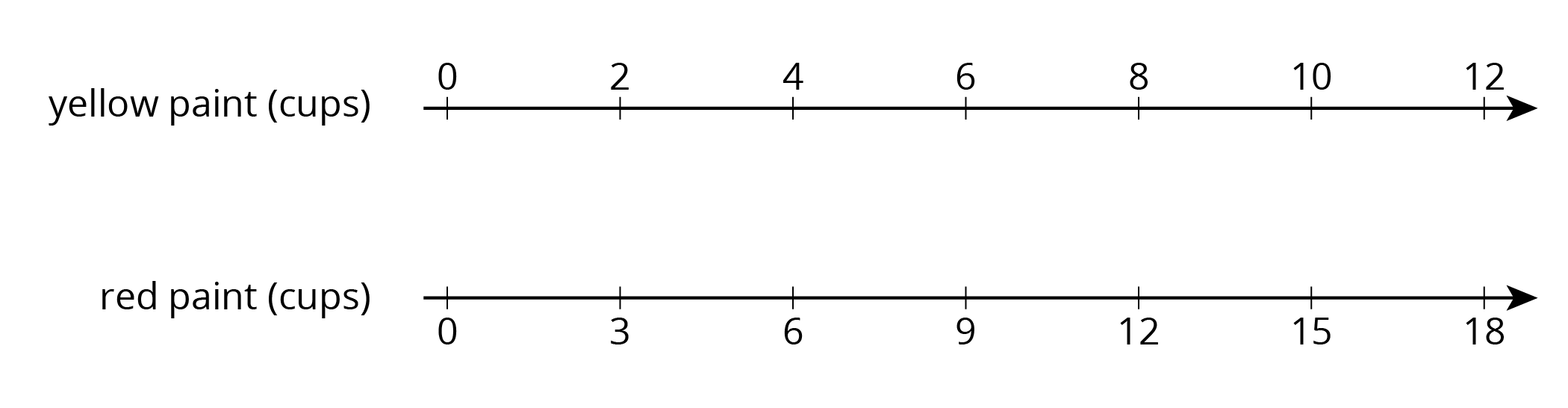
Problem 2
This double number line diagram shows the amount of flour and eggs needed for 1 batch of cookies.
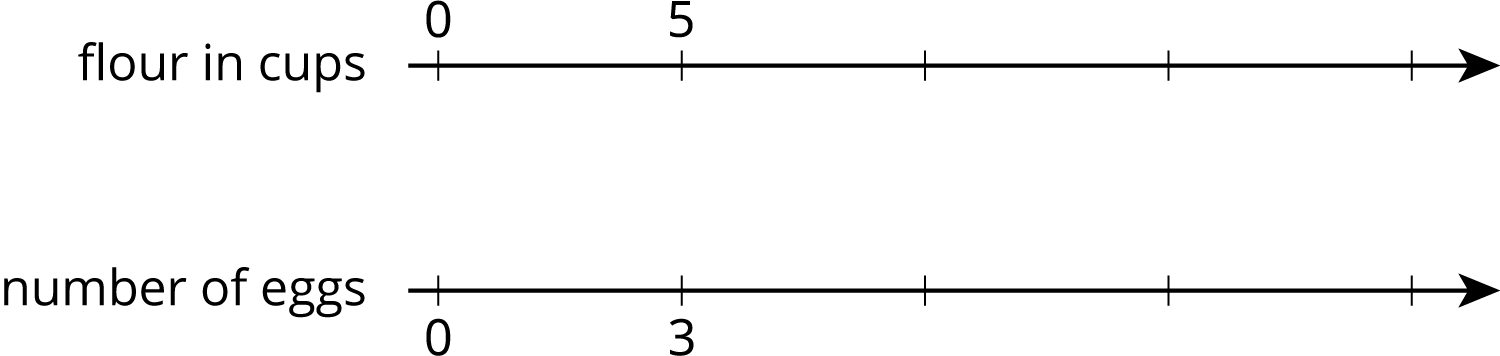
- Complete the diagram to show the amount of flour and eggs needed for 2, 3, and 4 batches of cookies.
- What is the ratio of cups of flour to eggs?
- How much flour and how many eggs are used in 4 batches of cookies?
- How much flour is used with 6 eggs?
- How many eggs are used with 15 cups of flour?
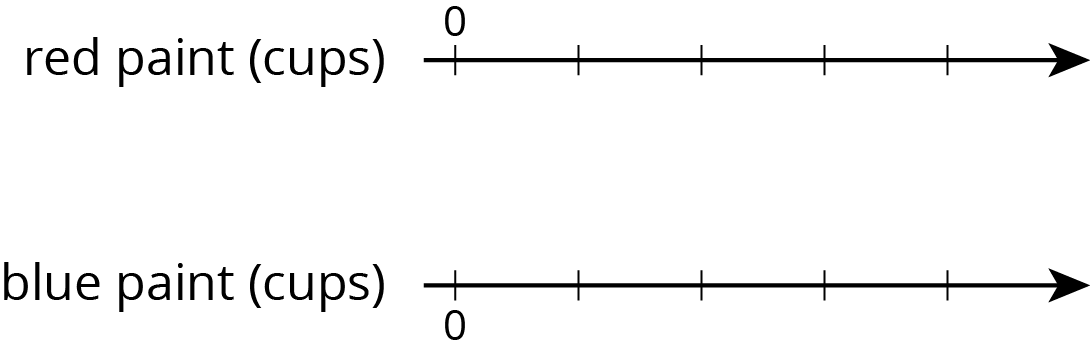
Problem 3
Here is a representation showing the amount of red and blue paint that make 2 batches of purple paint.
- On the double number line, label the tick marks to represent amounts of red and blue paint used to make batches of this shade of purple paint.

- How many batches are made with 12 cups of red paint?
- How many batches are made with 6 cups of blue paint?
Problem 4 (from Unit 2, Lesson 1)
Diego estimates that there will need to be 3 pizzas for every 7 kids at his party. Select all the statements that express this ratio.
- The ratio of kids to pizzas is $7:3$.
- The ratio of pizzas to kids is 3 to 7.
- The ratio of kids to pizzas is $3:7$.
- The ratio of pizzas to kids is 7 to 3.
- For every 7 kids there need to be 3 pizzas.
Problem 5 (from Unit 1, Lesson 6)
- Draw a parallelogram that is not a rectangle that has an area of 24 square units. Explain or show how you know the area is 24 square units.

- Draw a triangle that has an area of 24 square units. Explain or show how you know the area is 24 square units.

Lesson 7
Problem 1
A recipe for cinnamon rolls uses 2 tablespoons of sugar per teaspoon of cinnamon for the filling. Complete the double number line diagram to show the amount of cinnamon and sugar in 3, 4, and 5 batches.

Problem 2
One batch of meatloaf contains 2 pounds of beef and $\frac{1}{2}$ cup of bread crumbs. Complete the double number line diagram to show the amounts of beef and bread crumbs needed for 1, 2, 3, and 4 batches of meatloaf.
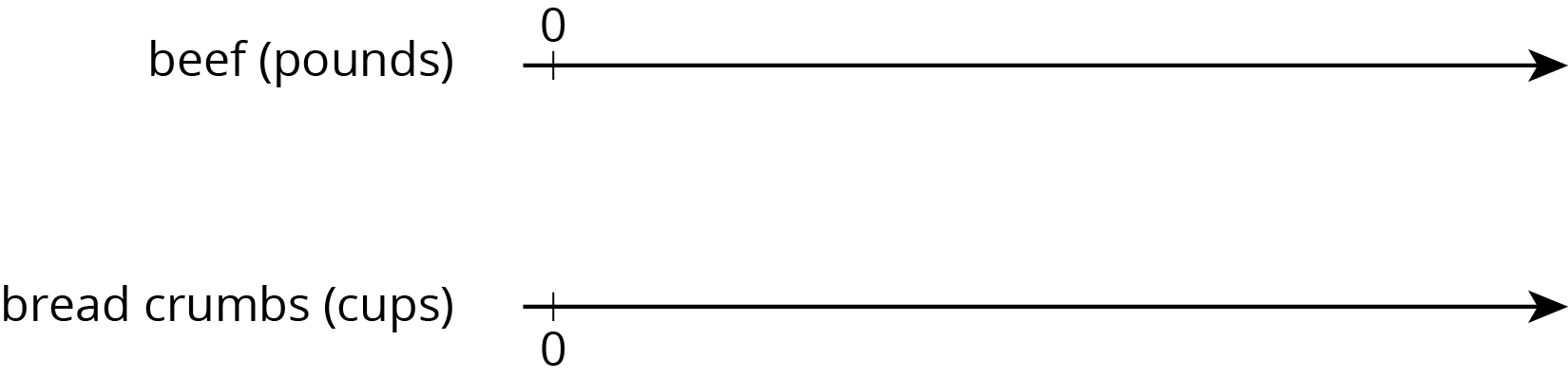
Problem 3
A recipe for tropical fruit punch says, “Combine 4 cups of pineapple juice with 5 cups of orange juice.”
- Create a double number showing the amount of each type of juice in 1, 2, 3, 4, and 5 batches of the recipe.
- If 12 cups of pineapple juice are used with 20 cups of orange juice, will the recipe taste the same? Explain your reasoning.
- The recipe also calls for $\frac13$ cup of lime juice for every 5 cups of orange juice. Add a line to your diagram to represent the amount of lime juice in different batches of tropical fruit punch.
Problem 4 (from Unit 2, Lesson 4)
One batch of pink paint uses 2 cups of red paint and 7 cups of white paint. Mai made a large amount of pink paint using 14 cups of red paint.
- How many batches of pink paint did she make?
- How many cups of white paint did she use?
Problem 5 (from Unit 2, Lesson 5)
- Find three different ratios that are equivalent to the ratio $3:11$.
- Explain why your ratios are equivalent.
Problem 6 (from Unit 2, Lesson 2)
Here is a diagram that represents the pints of red and yellow paint in a mixture.

Select all statements that accurately describe the diagram.
- The ratio of yellow paint to red paint is 2 to 6.
- For every 3 pints of red paint, there is 1 pint of yellow paint.
- For every pint of yellow paint, there are 3 pints of red paint.
- For every pint of yellow paint there are 6 pints of red paint.
- The ratio of red paint to yellow paint is $6:2$.
Lesson 8
Problem 1
In 2016, the cost of 2 ounces of pure gold was \$2,640. Complete the double number line to show the cost for 1, 3, and 4 ounces of gold.
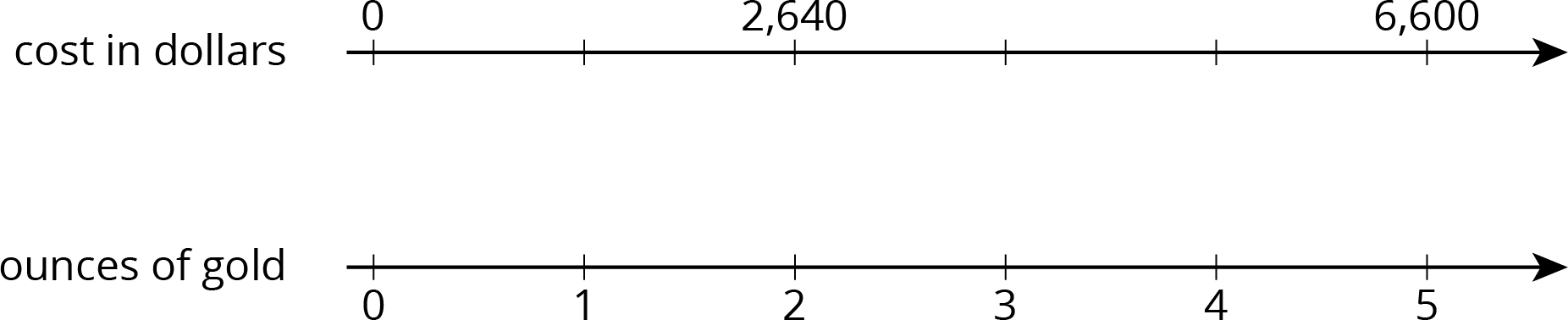
Problem 2
The double number line shows that 4 pounds of tomatoes cost \$14. Draw tick marks and write labels to show the prices of 1, 2, and 3 pounds of tomatoes.

Problem 3
4 movie tickets cost \$48. At this rate, what is the cost of:
- 5 movie tickets?
- 11 movie tickets?
Problem 4
Priya bought these items at the grocery store. Find each unit price.
- 12 eggs for \$3. How much is the cost per egg?
- 3 pounds of peanuts for \$7.50. How much is the cost per pound?
- 4 rolls of toilet paper for \$2. How much is the cost per roll?
-
10 apples for \$3.50. How much is the cost per apple?
Problem 5 (from Unit 2, Lesson 3)
Clare made a smoothie with 1 cup of yogurt, 3 tablespoons of peanut butter, 2 teaspoons of chocolate syrup, and 2 cups of crushed ice.
- Kiran tried to double this recipe. He used 2 cups of yogurt, 6 tablespoons of peanut butter, 5 teaspoons of chocolate syrup, and 4 cups of crushed ice. He didn’t think it tasted right. Describe how the flavor of Kiran's recipe compares to Clare's recipe.
- How should Kiran change the quantities that he used so that his smoothie tastes just like Clare's?
Problem 6 (from Unit 1, Lesson 15)
A drama club is building a wooden stage in the shape of a trapezoidal prism. The height of the stage is 2 feet. Some measurements of the stage are shown here.
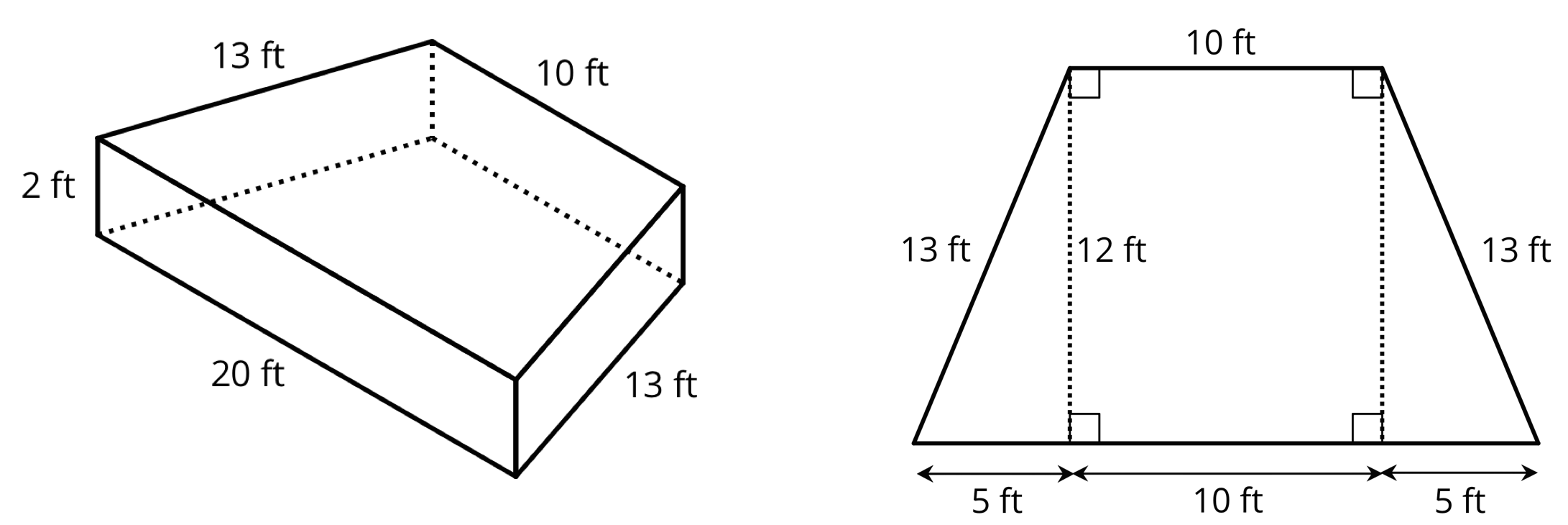
What is the area of all the faces of the stage, excluding the bottom? Show your reasoning. If you get stuck, consider drawing a net of the prism.
Lesson 9
Problem 1
Han ran 10 meters in 2.7 seconds. Priya ran 10 meters in 2.4 seconds.
- Who ran faster? Explain how you know.
- At this rate, how long would it take each person to run 50 meters? Explain or show your reasoning.
Problem 2
A scooter travels 30 feet in 2 seconds at a constant speed.
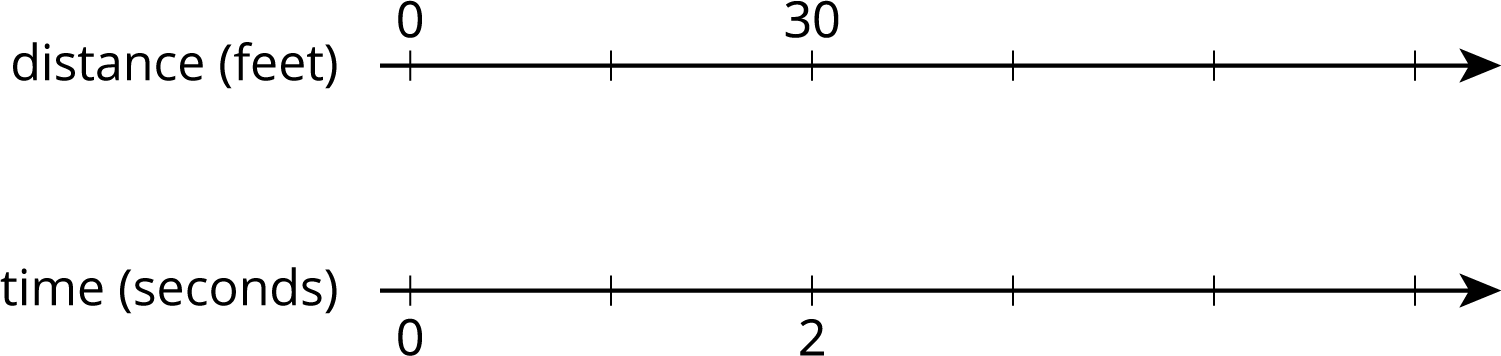
- What is the speed of the scooter in feet per second?
- Complete the double number line to show the distance the scooter travels after 1, 3, 4, and 5 seconds.
- A skateboard travels 55 feet in 4 seconds. Is the skateboard going faster, slower, or the same speed as the scooter?
Problem 3
A cargo ship traveled 150 nautical miles in 6 hours at a constant speed. How far did the cargo ship travel in one hour?
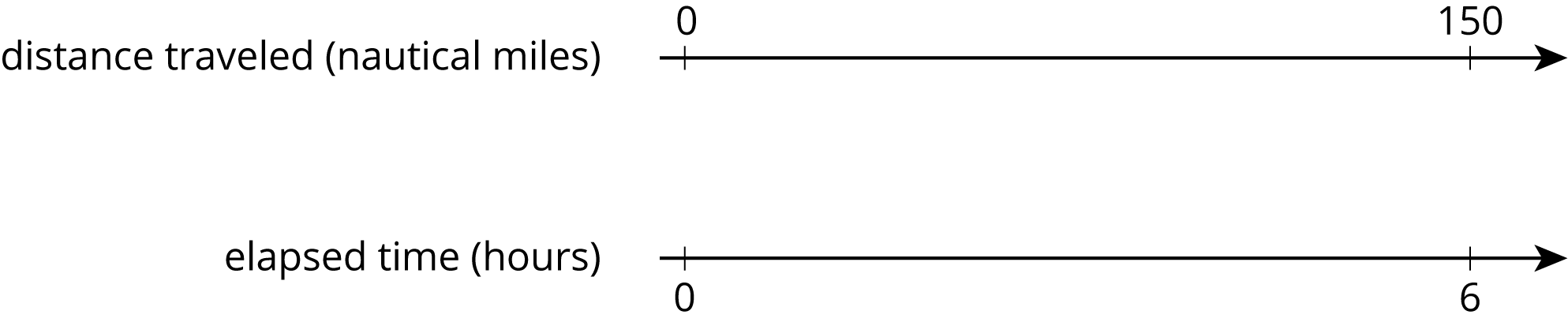
Problem 4 (from Unit 2, Lesson 3)
A recipe for pasta dough says, “Use 150 grams of flour per large egg.”
- How much flour is needed if 6 large eggs are used?
-
How many eggs are needed if 450 grams of flour are used?
Problem 5 (from Unit 2, Lesson 8)
The grocery store is having a sale on frozen vegetables. 4 bags are being sold for \$11.96. At this rate, what is the cost of:
- 1 bag
- 9 bags
Problem 6 (from Unit 2, Lesson 7)
A pet owner has 5 cats. Each cat has 2 ears and 4 paws.
- Complete the double number line to show the numbers of ears and paws for 1, 2, 3, 4, and 5 cats.
- If there are 3 cats in the room, what is the ratio of ears to paws?
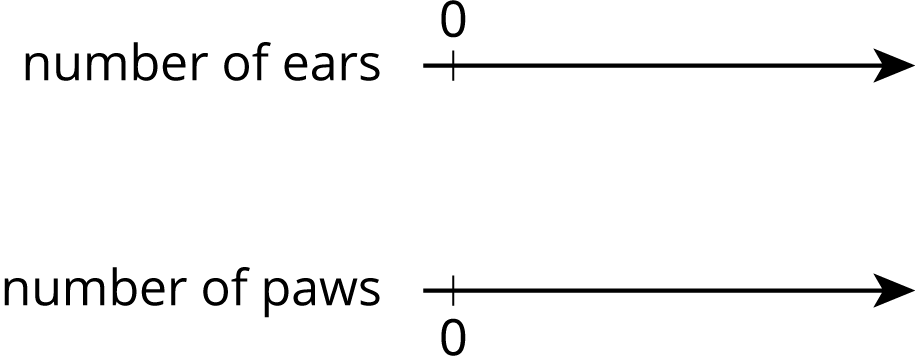
- If there are 4 cats in the room, what is the ratio of paws to ears?
- If all 5 cats are in the room, how many more paws are there than ears?
Problem 7 (from Unit 2, Lesson 5)
Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a representation that shows why they are equivalent ratios.
- $5:1$ and $15:3$
- $25:5$ and $10:2$
- $198:1,\!287$ and $2:13$
Lesson 10
Problem 1
A slug travels 3 centimeters in 3 seconds. A snail travels 6 centimeters in 6 seconds. Both travel at constant speeds. Mai says, “The snail was traveling faster because it went a greater distance.” Do you agree with Mai? Explain or show your reasoning.
Problem 2
If you blend 2 scoops of chocolate ice cream with 1 cup of milk, you get a milkshake with a stronger chocolate flavor than if you blended 3 scoops of chocolate ice cream with 2 cups of milk. Explain or show why.
Problem 3
There are 2 mixtures of light purple paint.
- Mixture A is made with 5 cups of purple paint and 2 cups of white paint.
- Mixture B is made with 15 cups of purple paint and 8 cups of white paint.
Which mixture is a lighter shade of purple? Explain your reasoning.
Problem 4
Problem 5 (from Unit 2, Lesson 9)
A plane travels at a constant speed. It takes 6 hours to travel 3,360 miles.
- What is the plane’s speed in miles per hour?
- At this rate, how many miles can it travel in 10 hours?
Problem 6 (from Unit 2, Lesson 8)
A pound of ground beef costs \$5. At this rate, what is the cost of:
- 3 pounds?
- $\frac 1 2$ pound?
- $\frac 1 4$ pound?
- $\frac 3 4$ pound?
- $3 \frac 3 4$ pounds?
Problem 7 (from Unit 2, Lesson 7)
In a triple batch of a spice mix, there are 6 teaspoons of garlic powder and 15 teaspoons of salt. Answer the following questions about the mix. If you get stuck, create a double number line.
- How much garlic powder is used with 5 teaspoons of salt?
- How much salt is used with 8 teaspoons of garlic powder?
- If there are 14 teaspoons of spice mix, how much salt is in it?
- How much more salt is there than garlic powder if 6 teaspoons of garlic powder are used?
Lesson 11
Problem 1
Complete the table to show the amounts of yellow and red paint needed for different-sized batches of the same shade of orange paint.
| yellow paint (quarts) | red paint (quarts) | |
|---|---|---|
| row 1 | 5 | 6 |
| row 2 | ||
| row 3 | ||
| row 4 |
Explain how you know that these amounts of yellow paint and red paint will make the same shade of orange as the mixture in the first row of the table.
Problem 2
A car travels at a constant speed, as shown on the double number line.
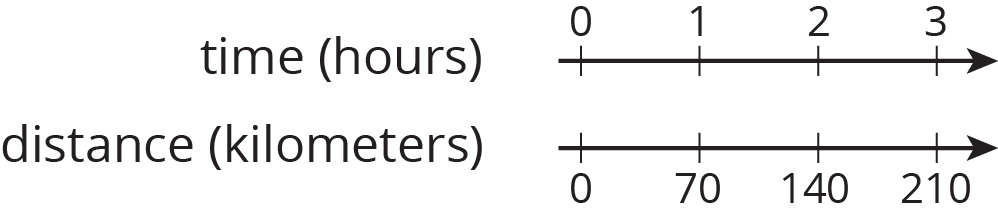
How far does the car travel in 14 hours? Explain or show your reasoning.
Problem 3
The olive trees in an orchard produce 3,000 pounds of olives a year. It takes 20 pounds of olives to make 3 liters of olive oil. How many liters of olive oil can this orchard produce in a year? If you get stuck, consider using the table.
| olives (pounds) | olive oil (liters) | |
|---|---|---|
| row 1 | 20 | 3 |
| row 2 | 100 | |
| row 3 | 3,000 |
Problem 4 (from Unit 2, Lesson 6)
At a school recess, there needs to be a ratio of 2 adults for every 24 children on the playground. The double number line represents the number of adults and children on the playground at recess.
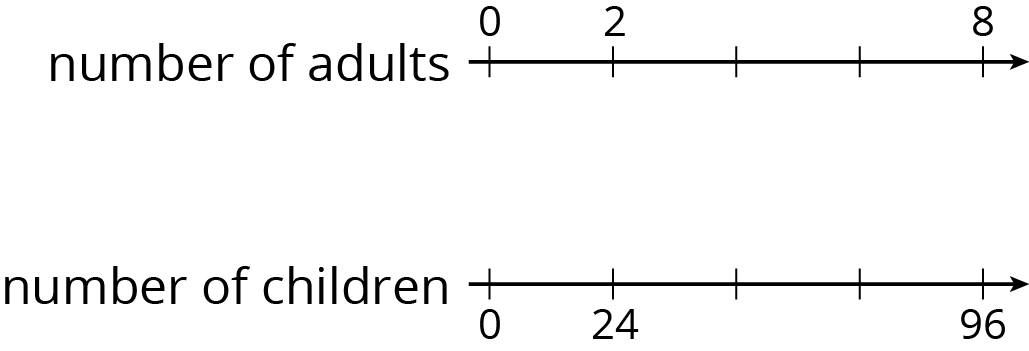
- Label each remaining tick mark with its value.
- How many adults are needed if there are 72 children? Circle your answer on the double number line.
Problem 5 (from Unit 2, Lesson 10)
While playing basketball, Jada’s heart rate goes up to 160 beats per minute. While jogging, her heart beats 25 times in 10 seconds. Assuming her heart beats at a constant rate while jogging, which of these activities resulted in a higher heart rate? Explain your reasoning.
Problem 6 (from Unit 2, Lesson 8)
A shopper bought the following items at the farmer’s market:
- 6 ears of corn for \$1.80. What was the cost per ear?
- 12 apples for \$2.88. What was the cost per apple?
- 5 tomatoes for \$3.10. What was the cost per tomato?
Lesson 12
Problem 1
Priya collected 2,400 grams of pennies in a fundraiser. Each penny has a mass of 2.5 grams. How much money did Priya raise? If you get stuck, consider using the table.
| number of pennies | mass in grams | |
|---|---|---|
| row 1 | 1 | 2.5 |
| row 2 | ||
| row 3 | ||
| row 4 | ||
| row 5 | ||
| row 6 | 2,400 |
Problem 2
Kiran reads 5 pages in 20 minutes. He spends the same amount of time per page. How long will it take him to read 11 pages? If you get stuck, consider using the table.
| time in minutes | number of pages | |
|---|---|---|
| row 1 | 20 | 5 |
| row 2 | 1 | |
| row 3 | 11 |
Problem 3
Mai is making personal pizzas. For 4 pizzas, she uses 10 ounces of cheese.
| number of pizzas | ounces of cheese | |
|---|---|---|
| row 1 | 4 | 10 |
| row 2 | ||
| row 3 |
a. How much cheese does Mai use per pizza?
b. At this rate, how much cheese will she need to make 15 pizzas?
Problem 4
Clare is paid \$90 for 5 hours of work. At this rate, how many seconds does it take for her to earn 25 cents?
Problem 5 (from Unit 2, Lesson 10)
A car that travels 20 miles in $\frac12$ hour at constant speed is traveling at the same speed as a car that travels 30 miles in $\frac34$ hour at a constant speed. Explain or show why.
Problem 6 (from Unit 2, Lesson 6)
Lin makes her favorite juice blend by mixing cranberry juice with apple juice in the ratio shown on the double number line. Complete the diagram to show smaller and larger batches that would taste the same as Lin's favorite blend.
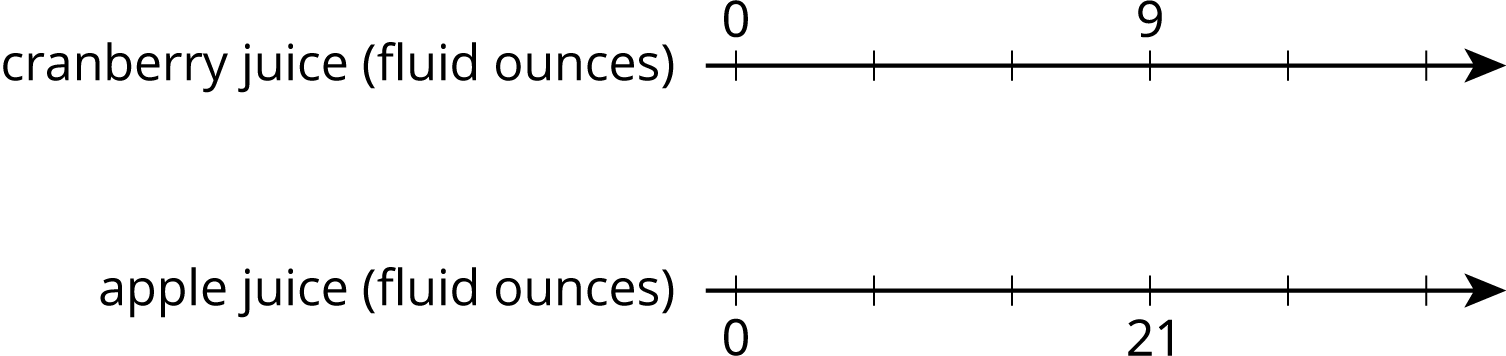
Problem 7 (from Unit 2, Lesson 5)
Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a representation that shows why they are equivalent ratios.
- $600:450$ and $60:45$
- $60:45$ and $4:3$
- $600:450$ and $4:3$
Lesson 13
Problem 1
The double number line shows how much water and how much lemonade powder to mix to make different amounts of lemonade.

Make a table that represents the same situation.
Problem 2
A bread recipe uses 3 tablespoons of olive oil for every 2 cloves of crushed garlic.
- Complete the table to show different-sized batches of bread that taste the same as the recipe.
- Draw a double number line that represents the same situation.
- Which representation do you think works better in this situation? Explain why.
| olive oil (tablespoons) | crushed garlic (cloves) | |
|---|---|---|
| row 1 | 3 | 2 |
| row 2 | 1 | |
| row 3 | 2 | |
| row 4 | 5 | |
| row 5 | 10 |
Problem 3
Clare travels at a constant speed, as shown on the double number line.
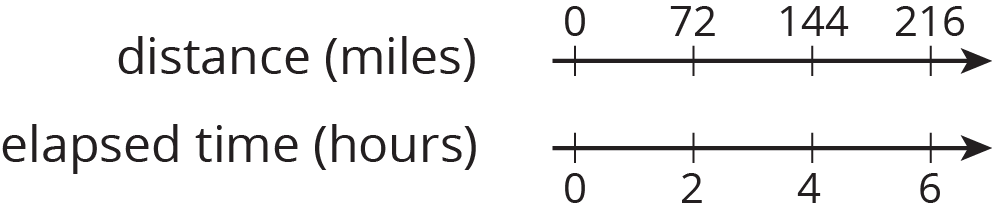
At this rate, how far does she travel in each of these intervals of time? Explain or show your reasoning. If you get stuck, consider using a table.
- 1 hour
- 3 hours
- 6.5 hours
Problem 4 (from Unit 2, Lesson 9)
Lin and Diego travel in cars on the highway at constant speeds. In each case, decide who was traveling faster and explain how you know.
- During the first half hour, Lin travels 23 miles while Diego travels 25 miles.
- After stopping for lunch, they travel at different speeds. To travel the next 60 miles, it takes Lin 65 minutes and it takes Diego 70 minutes.
Problem 5 (from Unit 2, Lesson 3)
A sports drink recipe calls for $\frac{5}{3}$ tablespoons of powdered drink mix for every 12 ounces of water. How many batches can you make with 5 tablespoons of drink mix and 36 ounces of water? Explain your reasoning.
Problem 6 (from Unit 1, Lesson 18)
In this cube, each small square has side length 1 unit.
- What is the surface area of this cube?
- What is the volume of this cube?

Lesson 14
Problem 1
A chef is making pickles. He needs 15 gallons of vinegar. The store sells 2 gallons of vinegar for \$3.00 and allows customers to buy any amount of vinegar. Decide whether each of the following ratios correctly represents the price of vinegar.
- 4 gallons to \$3.00
- 1 gallon to \$1.50
- 30 gallons to \$45.00
- \$2.00 to 30 gallons
- \$1.00 to $\frac23$ gallon
Problem 2
A caterer needs to buy 21 pounds of pasta to cater a wedding. At a local store, 8 pounds of pasta cost \$12. How much will the caterer pay for the pasta there?
- Write a ratio for the given information about the cost of pasta.
- Would it be more helpful to write an equivalent ratio with 1 pound of pasta as one of the numbers, or with \$1 as one of the numbers? Explain your reasoning, and then write that equivalent ratio.
- Find the answer and explain or show your reasoning.
Problem 3
Lin is reading a 47-page book. She read the first 20 pages in 35 minutes.
- If she continues to read at the same rate, will she be able to complete this book in under 1 hour?
-
If so, how much time will she have left? If not, how much more time is needed? Explain or show your reasoning.
Problem 4
Diego can type 140 words in 4 minutes.
- At this rate, how long will it take him to type 385 words?
- How many words can he type in 15 minutes?
If you get stuck, consider creating a table.
Problem 5 (from Unit 2, Lesson 10)
A train that travels 30 miles in $\frac13$ hour at a constant speed is going faster than a train that travels 20 miles in $\frac12$ hour at a constant speed. Explain or show why.
Problem 6 (from Unit 1, Lesson 14)
Find the surface area of the polyhedron that can be assembled from this net. Show your reasoning.
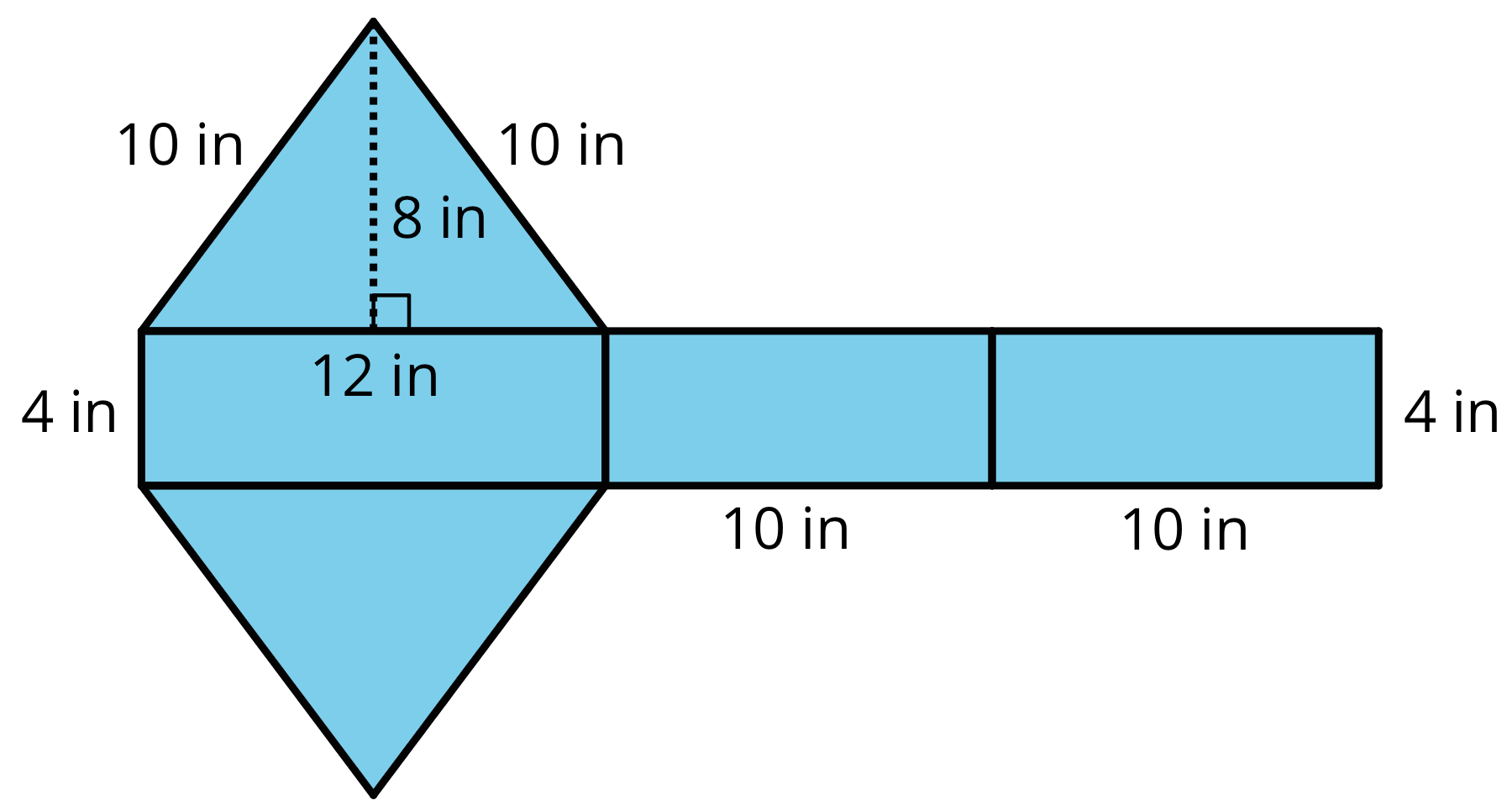
Lesson 15
Problem 1
Here is a tape diagram representing the ratio of red paint to yellow paint in a mixture of orange paint.
- What is the ratio of yellow paint to red paint?
- How many total cups of orange paint will this mixture yield?

Problem 2
At the kennel, the ratio of cats to dogs is $4:5$. There are 27 animals in all. Here is a tape diagram representing this ratio.

- What is the value of each small rectangle?
- How many dogs are at the kennel?
- How many cats are at the kennel?
Problem 3
Problem 4 (from Unit 2, Lesson 12)
Noah entered a 100-mile bike race. He knows he can ride 32 miles in 160 minutes. At this rate, how long will it take him to finish the race? Use each table to find the answer. Next, explain which table you think works better in finding the answer.
Table A:
| distance (miles) | elapsed time (minutes) | |
|---|---|---|
| row 1 | 32 | 160 |
| row 2 | 1 | |
| row 3 | 100 |
Table B:
| distance (miles) | elapsed time (minutes) | |
|---|---|---|
| row 1 | 32 | 160 |
| row 2 | 96 | |
| row 3 | 4 | |
| row 4 | 100 |
Problem 5 (from Unit 2, Lesson 13)
A cashier worked an 8-hour day, and earned \$58.00. The double number line shows the amount she earned for working different numbers of hours. For each question, explain your reasoning.
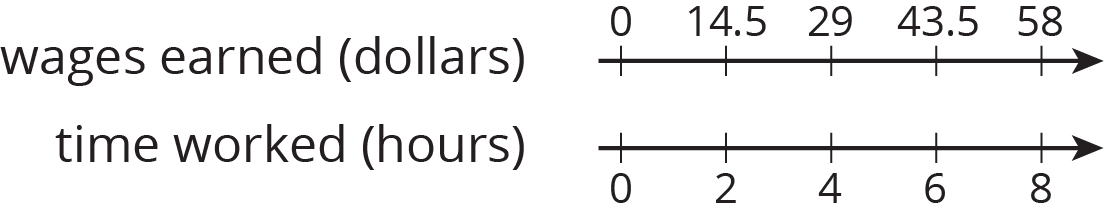
- How much does the cashier earn per hour?
- How much does the cashier earn if she works 3 hours?
Problem 6 (from Unit 2, Lesson 10)
A grocery store sells bags of oranges in two different sizes.
- The 3-pound bags of oranges cost \$4.
- The 8-pound bags of oranges for \$9.
Lesson 16
Problem 1
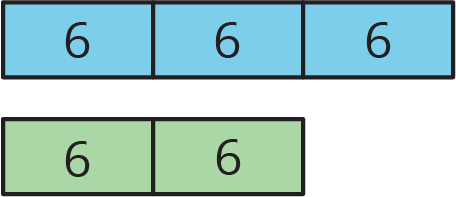
Describe a situation that could be represented with this tape diagram.
Problem 2
There are some nickels, dimes, and quarters in a large piggy bank. For every 2 nickels there are 3 dimes. For every 2 dimes there are 5 quarters. There are 500 coins total.
- How many nickels, dimes, and quarters are in the piggy bank? Explain your reasoning.
- How much are the coins in the piggy bank worth?
Problem 3
Two horses start a race at the same time. Horse A gallops at a steady rate of 32 feet per second and Horse B gallops at a steady rate of 28 feet per second. After 5 seconds, how much farther will Horse A have traveled? Explain or show your reasoning.
Problem 4 (from Unit 2, Lesson 10)
Problem 5 (from Unit 1, Lesson 15)
Which polyhedron can be assembled from this net?
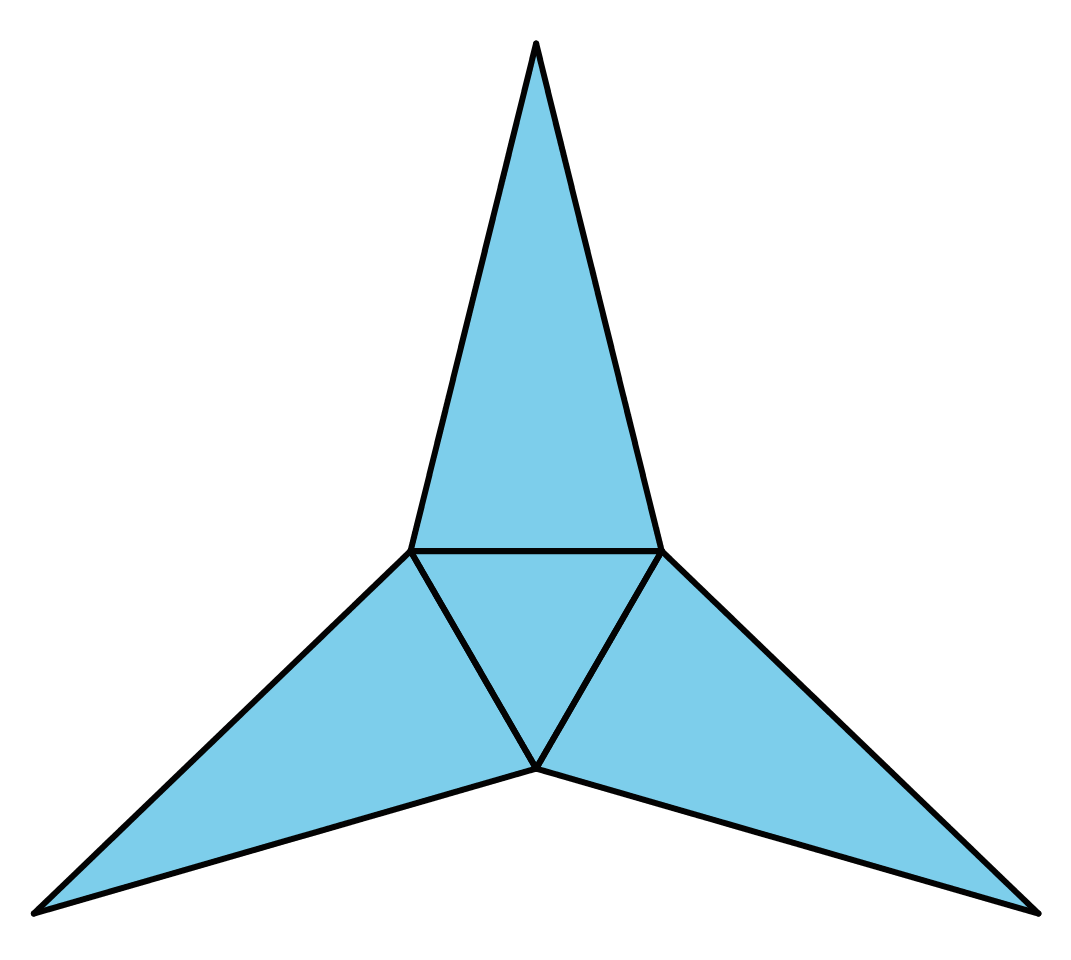
- A triangular pyramid
- A trapezoidal prism
- A rectangular pyramid
- A triangular prism
Problem 6 (from Unit 1, Lesson 10)
Find the area of the triangle. Show your reasoning. If you get stuck, consider drawing a rectangle around the triangle.

Lesson 17
No practice problems for this lesson.