4.1: Number Talk: Fractions of a Number
Find the values mentally.
$\frac14$ of 32
$\frac34$ of 32
$\frac38$ of 32
$\frac38$ of 64
Let’s convert measurements to different units.
Find the values mentally.
$\frac14$ of 32
$\frac34$ of 32
$\frac38$ of 32
$\frac38$ of 64
Elena and her mom are on a road trip outside the United States. Elena sees this road sign.
Elena’s mom is driving 75 miles per hour when she gets pulled over for speeding.

The police officer explains that 8 kilometers is approximately 5 miles.
A veterinarian uses weights in kilograms to figure out what dosages of medicines to prescribe for animals. For every 10 kilograms, there are 22 pounds.
Calculate each animal’s weight in kilograms. Explain or show your reasoning. If you get stuck, consider drawing a double number line or table.
Diego is trying to follow a recipe, but he cannot find any measuring cups! He only has a tablespoon. In the cookbook, it says that 1 cup equals 16 tablespoons.
How could Diego use the tablespoon to measure out these ingredients?
Diego also adds the following ingredients. How many cups of each did he use?
When we measure something in two different units, the measurements form an equivalent ratio. We can reason with these equivalent ratios to convert measurements from one unit to another.
Suppose you cut off 20 inches of hair. Your Canadian friend asks how many centimeters of hair that was. Since 100 inches equal 254 centimeters, we can use equivalent ratios to find out how many centimeters equal 20 inches.
Using a double number line:
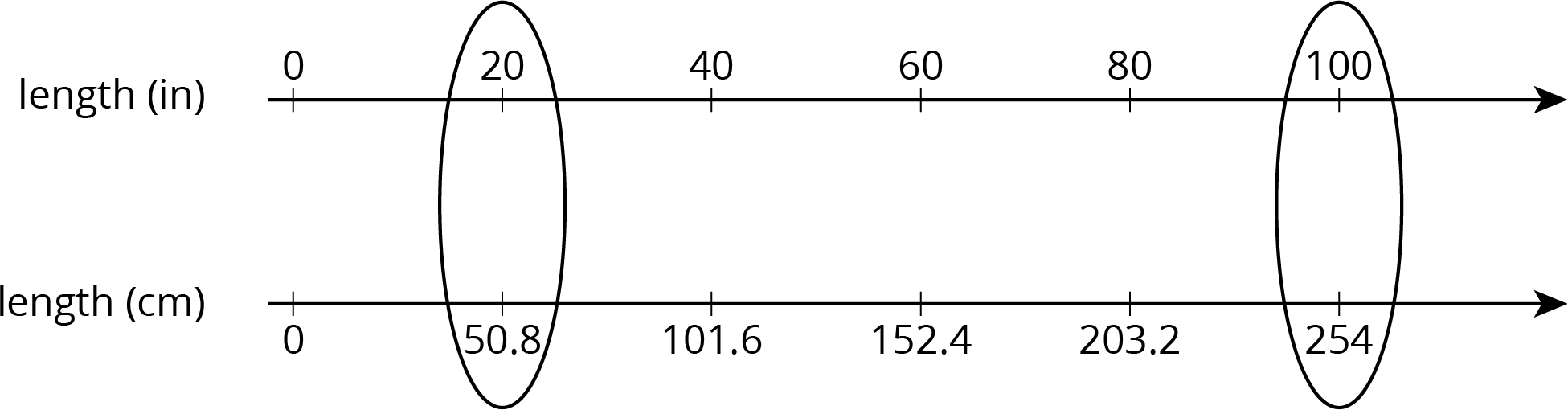
Using a table:
| length (in) | length (cm) | |
|---|---|---|
| row 1 | 100 | 254 |
| row 2 | 1 | 2.54 |
| row 3 | 20 | 50.8 |