- How many copies of this flower pattern could you build if you had 30 yellow hexagons, 50 red trapezoids, and 60 green triangles?
- Of which shape would you have the most left over?
Unit 3: Practice Problem Sets
Lesson 1
Problem 1
An elevator travels 310 feet in 10 seconds. At that speed, how far can this elevator travel in 12 seconds? Explain your reasoning.
Problem 2
Han earns \$33.00 for babysitting 4 hours. At this rate, how much will he earn if he babysits for 7 hours? Explain your reasoning.
Problem 3
The cost of 5 cans of dog food is \$4.35. At this price, how much do 11 cans of dog food cost? Explain your reasoning.
Problem 4
A restaurant has 26 tables in its dining room. It takes the waitstaff 10 minutes to clear and set 4 tables. At this rate, how long will it take the waitstaff to clear and set all the tables in the dining room? Explain or show your reasoning.
Problem 5 (from Unit 2, Lesson 16)
A sandwich shop serves 4 ounces of meat and 3 ounces of cheese on each sandwich. After making sandwiches for an hour, the shop owner has used 91 combined ounces of meat and cheese.
-
How many combined ounces of meat and cheese are used on each sandwich?
- How many sandwiches were made in the hour?
- How many ounces of meat were used?
- How many ounces of cheese were used?
Problem 6 (from Unit 2, Lesson 14)
Here is a flower made up of yellow hexagons, red trapezoids, and green triangles.
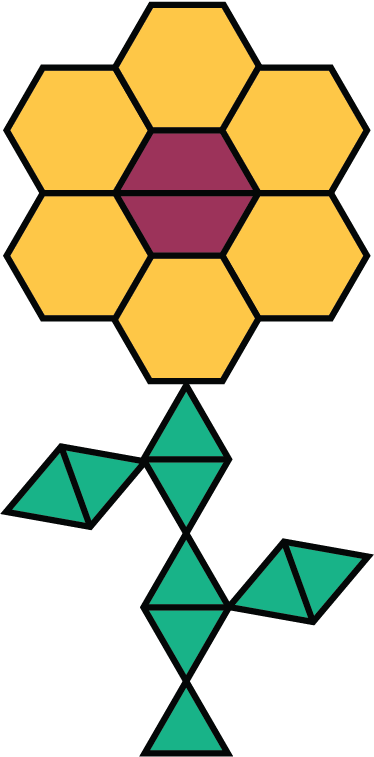
Problem 7 (from Unit 1, Lesson 16)
Match each quantity in the first list with an appropriate unit of measurement from the second list.
- the perimeter of a baseball field
- the area of a bed sheet
- the volume of a refrigerator
- the surface area of a tissue box
- the length of a spaghetti noodle
- the volume of a large lake
- the surface area of the the moon
- centimeters (cm)
- cubic feet (cu ft)
- cubic kilometers (cu km)
- meters (m)
- square feet (sq ft)
- square inches (sq in)
- square kilometers (sq km)
Lesson 2
Problem 1
Select the unit from the list that you would use to measure each object.
- The length of a pencil
- The weight or mass of a pencil
- The volume of a pencil
- The weight or mass of a hippopotamus
- The length of a hippopotamus
- The length of a fingernail clipping
- The weight or mass of a fingernail clipping
- The volume of a sink
- The volume of a bowl
- The length of a chalkboard or whiteboard
- The weight or mass of a chalkboard or whiteboard
- The length of the border between the United States and Canada
- centimeters
- cups
- feet
- gallons
- grams
- inches
- kilograms
- kilometers
- liters
- meters
- miles
- milliliters
- millimeters
- ounces
- pounds
- quarts
- tons
- yards
Problem 2
When this pet hamster is placed on a digital scale, the scale reads 1.5.

What could be the units?
Problem 3
Circle the larger unit of measure. Then, determine if the unit measures distance, volume, or weight (mass).
- meter or kilometer
- yard or foot
- cup or quart
- pound or ounce
- liter or milliliter
- gram or kilogram
Problem 4 (from Unit 2, Lesson 15)
Elena mixes 5 cups of apple juice with 2 cups of sparkling water to make sparkling apple juice. For a party, she wants to make 35 cups of sparkling apple juice. How much of each ingredient should Elena use? Explain or show your reasoning.
Problem 5 (from Unit 2, Lesson 12)
Lin bought 3 hats for \$22.50. At this rate, how many hats could she buy with \$60.00? If you get stuck, try using the table.
| number of hats | price in dollars | |
|---|---|---|
| row 1 | ||
| row 2 | ||
| row 3 | ||
| row 4 |
Problem 6 (from Unit 2, Lesson 9)
Light travels about 180 million kilometers in 10 minutes. How far does it travel in 1 minute? How far does it travel in 1 second? Show your reasoning.
Lesson 3
Problem 1 (from Unit 3, Lesson 2)
Decide if each is a measurement of length, area, volume, or weight (or mass).
- How many centimeters across a handprint
- How many square inches of paper needed to wrap a box
- How many gallons of water in a fish tank
- How many pounds in a bag of potatoes
- How many feet across a swimming pool
- How many ounces in a bag of grapes
- How many liters in a punch bowl
- How many square feet of grass in a lawn
Problem 2
Clare says, “This classroom is 11 meters long. A meter is longer than a yard, so if I measure the length of this classroom in yards, I will get less than 11 yards.” Do you agree with Clare? Explain your reasoning.
Problem 3
Tyler’s height is 57 inches. What could be his height in centimeters? Explain your reasoning.
- 22.4
- 57
- 144.8
-
3,551
Problem 4
A large soup pot holds 20 quarts. What could be its volume in liters?
- 7.57
- 19
- 21
- 75.7
Problem 5
Clare wants to mail a package that weighs $4\frac12$ pounds. What could this weight be in kilograms?
- 2.04
- 4.5
- 9.92
- 4,500
Problem 6 (from Unit 2, Lesson 13)
Noah bought 15 baseball cards for \$9.00. Assuming each baseball card costs the same amount, answer the following questions.
- At this rate, how much will 30 baseball cards cost? Explain your reasoning.
- At this rate, how much will 12 baseball cards cost? Explain your reasoning.
- Do you think this information would be better represented using a table or a double number line? Explain your reasoning.
Problem 7 (from Unit 2, Lesson 9)
Jada traveled 135 miles in 3 hours. Andre traveled 228 miles in 6 hours. Both Jada and Andre traveled at a constant speed.
- How far did Jada travel in 1 hour?
- How far did Andre travel in 1 hour?
- Who traveled faster? Explain or show your reasoning.
Lesson 4
Problem 1
Priya’s family exchanged 250 dollars for 4,250 pesos. Priya bought a sweater for 510 pesos. How many dollars did the sweater cost?
| pesos | dollars | |
|---|---|---|
| row 1 | 4,250 | 250 |
| row 2 | 25 | |
| row 3 | 1 | |
| row 4 | 3 | |
| row 5 | 510 |
Problem 2
There are 3,785 milliliters in 1 gallon, and there are 4 quarts in 1 gallon. For each question, explain or show your reasoning.
- How many milliliters are in 3 gallons?
- How many milliliters are in 1 quart?
Problem 3
Problem 4
Tyler has a baseball bat that weighs 28 ounces. Find this weight in kilograms and in grams. (Note: 1 kilogram $\approx$ 35 ounces)
Problem 5 (from Unit 3, Lesson 1)
Identify whether each unit measures length, volume, or weight (or mass).
- Mile
- Cup
- Pound
- Centimeter
- Liter
- Gram
- Pint
- Yard
- Kilogram
- Teaspoon
- Milliliter
Problem 6 (from Unit 2, Lesson 11)
A recipe for trail mix uses 7 ounces of almonds with 5 ounces of raisins. (Almonds and raisins are the only ingredients.) How many ounces of almonds would be in a one-pound bag of this trail mix? Explain or show your reasoning.
Problem 7 (from Unit 2, Lesson 9)
An ant can travel at a constant speed of 980 inches every 5 minutes.
- How far does the ant travel in 1 minute?
- At this rate, how far can the ant travel in 7 minutes?
Lesson 5
Problem 1
Mai and Priya were on scooters. Mai traveled 15 meters in 6 seconds. Priya travels 22 meters in 10 seconds. Who was moving faster? Explain your reasoning.
Problem 2
Here are the prices for cans of juice that are the same brand and the same size at different stores. Which store offers the best deal? Explain your reasoning.
Store X: 4 cans for \$2.48
Store Y: 5 cans for \$3.00
Store Z: 59 cents per can
Problem 3
Costs of homes can be very different in different parts of the United States.
- A 450-square-foot apartment in New York City costs \$540,000. What is the price per square foot? Explain or show your reasoning.
- A 2,100-square-foot home in Cheyenne, Wyoming, costs \$110 per square foot. How much does this home cost? Explain or show your reasoning.
Problem 4 (from Unit 3, Lesson 4)
There are 33.8 fluid ounces in a liter. There are 128 fluid ounces in a gallon. About how many liters are in a gallon?
- 2
- 3
- 4
- 5
Is your estimate larger or smaller than the actual number of liters in a gallon? Explain how you know.
Problem 5 (from Unit 3, Lesson 3)
Diego is 165 cm tall. Andre is 1.7 m tall. Who is taller, Diego or Andre? Explain your reasoning.
Problem 6 (from Unit 3, Lesson 2)
Name an object that could be about the same length as each measurement.
- 4 inches
- 6 feet
- 1 meter
- 5 yards
- 6 centimeters
- 2 millimeters
- 3 kilometers
Lesson 6
Problem 1
A pink paint mixture uses 4 cups of white paint for every 3 cups of red paint.
The table shows different quantities of red and white paint for the same shade of pink. Complete the table.
| white paint (cups) | red paint (cups) | |
|---|---|---|
| row 1 | 4 | 3 |
| row 2 | 1 | |
| row 3 | 1 | |
| row 4 | 4 | |
| row 5 | 5 |
Problem 2
A farm lets you pick 3 pints of raspberries for \$12.00.
- What is the cost per pint?
- How many pints do you get per dollar?
- At this rate, how many pints can you afford for \$20.00?
- At this rate, how much will 8 pints of raspberries cost?
Problem 3
Han and Tyler are following a polenta recipe that uses 5 cups of water for every 2 cups of cornmeal.
- Han says, “I am using 3 cups of water. I will need $1\frac15$ cups of cornmeal.”
- Tyler says, “I am using 3 cups of cornmeal. I will need $7\frac12$ cups of water.”
Do you agree with either of them? Explain your reasoning.
Problem 4
A large art project requires enough paint to cover 1,750 square feet. Each gallon of paint can cover 350 square feet. Each square foot requires $\frac{1}{350}$ of a gallon of paint.
Andre thinks he should use the rate $\frac{1}{350}$ gallons of paint per square foot to find how much paint they need. Do you agree with Andre? Explain or show your reasoning.
Problem 5 (from Unit 3, Lesson 5)
Andre types 208 words in 4 minutes. Noah types 342 words in 6 minutes. Who types faster? Explain your reasoning.
Problem 6 (from Unit 3, Lesson 5)
A corn vendor at a farmer's market was selling a bag of 8 ears of corn for \$2.56. Another vendor was selling a bag of 12 for \$4.32. Which bag is the better deal? Explain or show your reasoning.
Problem 7 (from Unit 3, Lesson 3)
A soccer field is 100 meters long. What could be its length in yards?
- 33.3
- 91
- 100
- 109
Lesson 7
Problem 1
A car travels 55 miles per hour for 2 hours. Complete the table.
| time (hours) | distance (miles) | miles per hour | |
|---|---|---|---|
| row 1 | 1 | 55 | 55 |
| row 2 | \(\frac12\) | ||
| row 3 | \(1\frac12\) | ||
| row 4 | 110 |
Problem 2
The table shows the amounts of onions and tomatoes in different-sized batches of a salsa recipe.
Elena notices that if she takes the number in the tomatoes column and divides it by the corresponding number in the onions column, she always gets the same result.
What is the meaning of the number that Elena has calculated?
| onions (ounces) | tomatoes (ounces) | |
|---|---|---|
| row 1 | 2 | 16 |
| row 2 | 4 | 32 |
| row 3 | 6 | 48 |
Problem 3
Problem 4
Complete the table so that the cost per banana remains the same.
| number of bananas |
cost in dollars |
unit price (dollars per banana) |
|
|---|---|---|---|
| row 1 | 4 | 0.50 | |
| row 2 | 6 | 0.50 | |
| row 3 | 7 | 0.50 | |
| row 4 | 10 | 0.50 | |
| row 5 | 10.00 | 0.50 | |
| row 6 | 16.50 | 0.50 |
Problem 5 (from Unit 3, Lesson 5)
Two planes travel at a constant speed. Plane A travels 2,800 miles in 5 hours. Plane B travels 3,885 miles in 7 hours. Which plane is faster? Explain your reasoning.
Problem 6 (from Unit 3, Lesson 6)
A car has 15 gallons of gas in its tank. The car travels 35 miles per gallon of gas. It uses $\frac{1}{35}$ of a gallon of gas to go 1 mile.
- How far can the car travel with 15 gallons? Show your reasoning.
- How much gas does the car use to go 100 miles? Show your reasoning.
Problem 7 (from Unit 3, Lesson 4)
A box of cereal weighs 600 grams. How much is this weight in pounds? Explain or show your reasoning. (Note: 1 kilogram = 2.2 pounds)
Lesson 8
Problem 1
A kangaroo hops 2 kilometers in 3 minutes. At this rate:
- How long does it take the kangaroo to travel 5 kilometers?
- How far does the kangaroo travel in 2 minutes?
Problem 2
Mai runs around a 400-meter track at a constant speed of 250 meters per minute. How many minutes does it take Mai to complete 4 laps of the track? Explain or show your reasoning.
Problem 3
At 10:00 a.m., Han and Tyler both started running toward each other from opposite ends of a 10-mile path along a river. Han runs at a pace of 12 minutes per mile. Tyler runs at a pace of 15 minutes per mile.
- How far does Han run after a half hour? After an hour?
- Do Han and Tyler meet on the path within 1 hour? Explain or show your reasoning.
Problem 4 (from Unit 2, Lesson 16)
Two skateboarders start a race at the same time. Skateboarder A travels at a steady rate of 15 feet per second. Skateboarder B travels at a steady rate of 22 feet per second. After 4 minutes, how much farther will Skateboarder B have traveled? Explain your reasoning.
Problem 5 (from Unit 3, Lesson 4)
There are 4 tablespoons in $\frac14$ cup. There are 2 cups in 1 pint. How many tablespoons are there in 1 pint? If you get stuck, consider drawing a double number line or making a table.
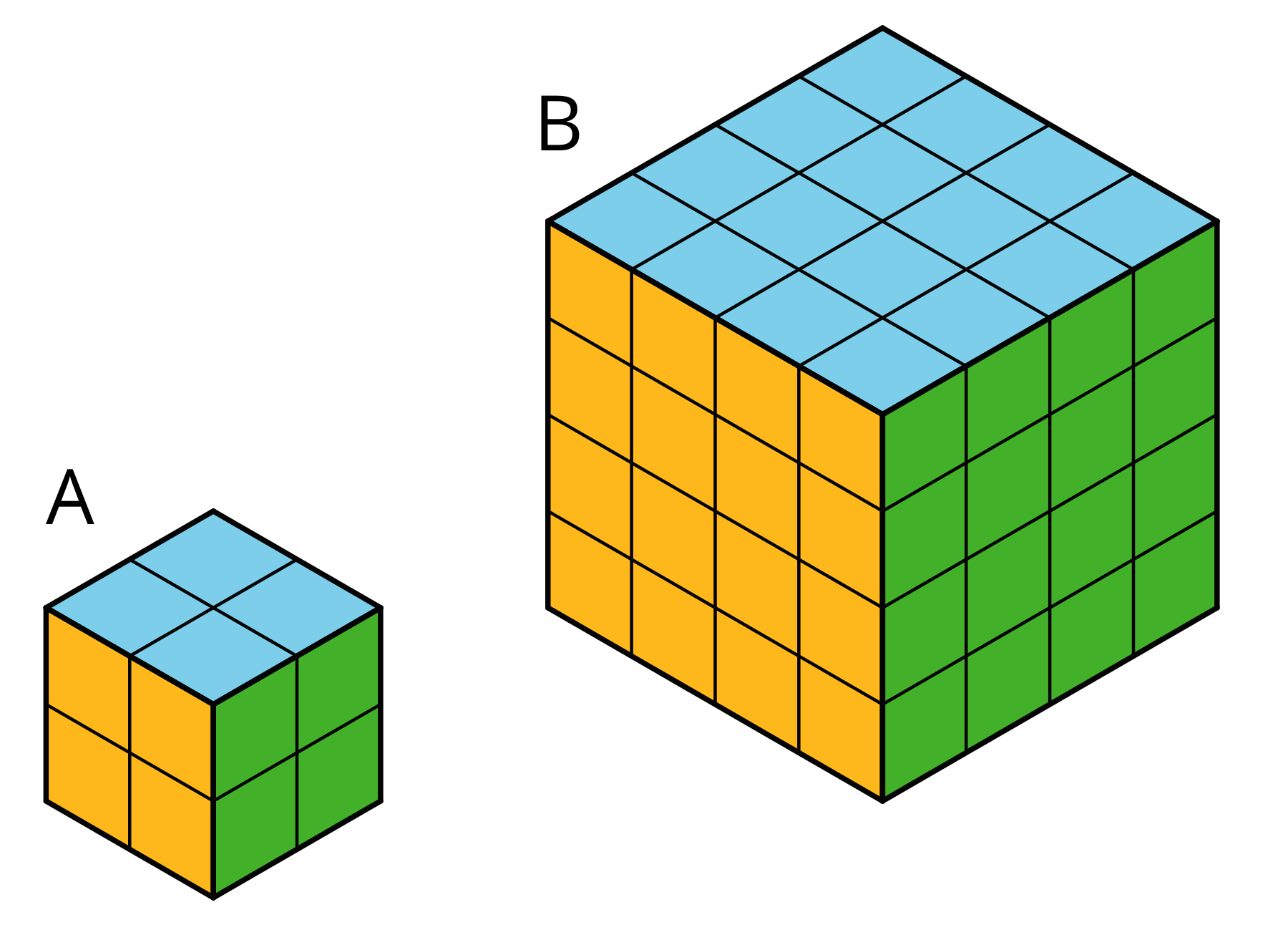
Problem 6 (from Unit 1, Lesson 12)
Two larger cubes are made out of unit cubes. Cube A is 2 by 2 by 2. Cube B is 4 by 4 by 4. The side length of Cube B is twice that of Cube A.
- Is the surface area of Cube B also twice that of Cube A? Explain or show your reasoning.
- Is the volume of Cube B also twice that of Cube A? Explain or show your reasoning.
Lesson 9
Problem 1
This package of sliced cheese costs \$2.97.
How much would a package with 18 slices cost at the same price per slice? Explain or show your reasoning.

Problem 2
A copy machine can print 480 copies every 4 minutes. For each question, explain or show your reasoning.
- How many copies can it print in 10 minutes?
- A teacher printed 720 copies. How long did it take to print?
Problem 3
Order these objects from heaviest to lightest. (Note: 1 pound = 16 ounces, 1 kilogram $\approx$ 2.2 pounds, and 1 ton = 2,000 pounds)
| item | weight | |
|---|---|---|
| row 1 | school bus | 9 tons |
| row 2 | horse | 1,100 pounds |
| row 3 | elephant | 5,500 kilograms |
| row 4 | grand piano | 15,840 ounces |
Problem 4 (from Unit 3, Lesson 5)
Andre sometimes mows lawns on the weekend to make extra money. Two weeks ago, he mowed a neighbor’s lawn for $\frac{1}{2}$ hour and earned \$10. Last week, he mowed his uncle’s lawn for $\frac{3}{2}$ hours and earned \$30. This week, he mowed the lawn of a community center for 2 hours and earned \$30.
Which jobs paid better than others? Explain your reasoning.
Problem 5 (from Unit 3, Lesson 1)
Calculate and express your answer in decimal form.
- $\frac12 \boldcdot 17$
- $\frac34 \boldcdot 200$
- $(0.2) \boldcdot 40$
- $(0.25) \boldcdot 60$
Problem 6 (from Unit 1, Lesson 11)
- Decompose this polygon so that its area can be calculated. All measurements are in centimeters.

- Calculate its area. Organize your work so that it can be followed by others.
Lesson 10
Problem 1
What percentage of a dollar is the value of each coin combination?
- 4 dimes
- 1 nickel and 3 pennies
- 5 quarters and 1 dime
Problem 2
-
List three different combinations of coins, each with a value of 30% of a dollar.
-
List two different combinations of coins, each with a value of 140% of a dollar.
Problem 3
The United States government used to make coins of many different values. For each coin, state its worth as a percentage of \$1.

- $\frac{1}{2}$ cent
- 3 cents
- 20 cents
- $\$2 \frac{1}{2}$
- \$5
Problem 4
Complete the double number to line show percentages of \$50.

Problem 5 (from Unit 3, Lesson 9)
Elena bought 8 tokens for \$4.40. At this rate:
- How many tokens could she buy with \$6.05?
- How much do 19 tokens cost?
Problem 6 (from Unit 3, Lesson 8)
A snail travels 10 cm in 4 minutes. At this rate:
- How long will it take the snail to travel 24 cm?
- How far does the snail travel in 6 minutes?
Problem 7 (from Unit 3, Lesson 7)
- 3 tacos cost \$18. Complete the table to show the cost of 4, 5, and 6 tacos at the same rate.
number of tacos cost in dollars rate in dollars per taco row 1 3 18 row 2 4 row 3 5 row 4 6 b. If you buy $t$ tacos for $c$ dollars, what is the unit rate?
Lesson 11
Problem 1
Solve each problem. If you get stuck, consider using the double number lines.
-
During a basketball practice, Mai attempted 40 free throws and was successful on 25% of them. How many successful free throws did she make?

-
Yesterday, Priya successfully made 12 free throws. Today, she made 150% as many. How many successful free throws did Priya make today?

Problem 2
A 16-ounce bottle of orange juice says it contains 200 milligrams of vitamin C, which is 250% of the daily recommended allowance of vitamin C for adults. What is 100% of the daily recommended allowance of vitamin C for adults?

Problem 3
Problem 4 (from Unit 3, Lesson 9)
Diego has a skateboard, scooter, bike, and go-cart. He wants to know which vehicle is the fastest. A friend records how far Diego travels on each vehicle in 5 seconds. For each vehicle, Diego travels as fast as he can along a straight, level path.
| vehicle | distance traveled | |
|---|---|---|
| row 1 | skateboard | 90 feet |
| row 2 | scooter | 1,020 inches |
| row 3 | bike | 4,800 centimeters |
| row 4 | go-cart | 0.03 kilometers |
- 100 inches equal 254 centimeters. What is the distance each vehicle traveled in centimeters?
- Rank the vehicles in order from fastest to slowest.
Problem 5 (from Unit 3, Lesson 7)
It takes 10 pounds of potatoes to make 15 pounds of mashed potatoes. At this rate:
- How many pounds of mashed potatoes can they make with 15 pounds of potatoes?
- How many pounds of potatoes are needed to make 50 pounds of mashed potatoes?
Lesson 12
Problem 1
Here is a tape diagram that shows how far two students walked.

- What percentage of Priya’s distance did Tyler walk?
- What percentage of Tyler’s distance did Priya walk?
Problem 2
A bakery makes 40 different flavors of muffins. 25% of the flavors have chocolate as one of the ingredients. Draw a tape diagram to show how many flavors have chocolate and how many don’t.
Problem 3
There are 70 students in the school band. 40% of them are sixth graders, 20% are seventh graders, and the rest are eighth graders.
- How many band members are sixth graders?
- How many band members are seventh graders?
- What percentage of the band members are eighth graders? Explain your reasoning.
Problem 4 (from Unit 3, Lesson 11)
Jada has a monthly budget for her cell phone bill. Last month she spent 120% of her budget, and the bill was \$60. What is Jada’s monthly budget? Explain or show your reasoning.
Problem 5 (from Unit 3, Lesson 9)
Which is a better deal, 5 tickets for \$12.50 or 8 tickets for \$20.16? Explain your reasoning.
Problem 6 (from Unit 3, Lesson 8)
An athlete runs 8 miles in 50 minutes on a treadmill. At this rate:
- How long will it take the athlete to run 9 miles?
- How far can the athlete run in 1 hour?
Lesson 13
Problem 1
-
How can you find 50% of a number quickly in your head?
-
Andre lives 1.6 km from school. What is 50% of 1.6 km?
-
Diego lives $\frac 1 2$ mile from school. What is 50% of $\frac 1 2$ mile?
Problem 2
There is a 10% off sale on laptop computers. If someone saves \$35 on a laptop, what was its original cost? If you get stuck, consider using the table.
| savings (dollars) | percentage | |
|---|---|---|
| row 1 | 35 | 10 |
| row 2 | ? | 100 |
Problem 3
Explain how to calculate these mentally.
- 15 is what percentage of 30?
- 3 is what percentage of 12?
- 6 is what percentage of 10?
Problem 4
Problem 5 (from Unit 3, Lesson 10)
Diego has 75% of \$10. Noah has 25% of \$30. Diego thinks he has more money than Noah, but Noah thinks they have an equal amount of money. Who is right? Explain your reasoning.
Problem 6 (from Unit 3, Lesson 8)
Lin and Andre start walking toward each other at the same time from opposite ends of 22-mile walking trail. Lin walks at a speed of 2.5 miles per hour. Andre walks at a speed of 3 miles per hour.
Here is a table showing the distances traveled and how far apart Lin and Andre were over time. Use the table to find how much time passes before they meet.
| elapsed time (hour) | Lin’s distance (miles) | Andre’s distance (miles) | distance apart (miles) | |
|---|---|---|---|---|
| row 1 | 0 | 0 | 0 | 22 |
| row 2 | 1 | 2.5 | 3 | 16.5 |
| row 3 | ||||
| row 4 | ||||
| row 5 | 0 |
Lesson 14
Problem 1
For each problem, explain or show your reasoning.
- 160 is what percentage of 40?
- 40 is 160% of what number?
- What number is 40% of 160?
Problem 2
A store is having a 20%-off sale on all merchandise. If Mai buys one item and saves \$13, what was the original price of her purchase? Explain or show your reasoning.
Problem 3
The original price of a scarf was \$16. During a store-closing sale, a shopper saved \$12 on the scarf. What percentage discount did she receive? Explain or show your reasoning.
Problem 4
Select all the expressions whose value is larger than 100.
- 120% of 100
- 50% of 150
- 150% of 50
- 20% of 800
- 200% of 30
- 500% of 400
- 1% of 1,000
Problem 5 (from Unit 3, Lesson 8)
An ant travels at a constant rate of 30 cm every 2 minutes.
- At what pace does the ant travel per centimeter?
- At what speed does the ant travel per minute?
Problem 6 (from Unit 3, Lesson 4)
Is 3$\frac{1}{2}$ cups more or less than 1 liter? Explain or show your reasoning. (Note: 1 cup $\approx$ 236.6 milliliters)
Problem 7 (from Unit 3, Lesson 2)
Name a unit of measurement that is about the same size as each object.
-
The distance of a doorknob from the floor is about 1 _____________.
-
The thickness of a fingernail is about 1 _____________.
-
The volume of a drop of honey is about 1 _____________.
-
The weight or mass of a pineapple is about 1 _____________.
-
The thickness of a picture book is about 1 _____________.
-
The weight or mass of a buffalo is about 1 _____________.
-
The volume of a flower vase is about 1 _____________.
-
The weight or mass of 20 staples is about 1 _____________.
-
The volume of a melon is about 1 _____________.
-
The length of a piece of printer paper is about 1 _____________.
Lesson 15
Problem 1
- To find 40% of 75, Priya calculates $\frac{2}{5} \boldcdot 75$. Does her calculation give the correct value for 40% of 75? Explain or show how you know.
- If $x$ represents a number, does $\frac{2}{5} \boldcdot x$ always represent 40% of that number? Explain your reasoning.
Problem 2
Han spent 75 minutes practicing the piano over the weekend. For each question, explain or show your reasoning.
- Priya practiced the violin for 152% as much time as Han practiced the piano. How long did she practice?
- Tyler practiced the clarinet for 64% as much time as Han practiced the piano. How long did he practice?
Problem 3
Problem 4
Order from greatest to least:
- 55% of 180
- 300% of 26
- 12% of 700
Problem 5 (from Unit 3, Lesson 14)
Complete each statement.
- 20% of 60 is ________
- 25% of ________ is 6
- ________% of 100 is 14
- 50% of 90 is ________
- 10% of ________ is 7
- 30% of 70 is ________
Problem 6 (from Unit 3, Lesson 9)
A shopper needs 24 sandwich rolls. The store sells identical rolls in 2 differently sized packages. They sell a six-pack for \$5.28 and a four-pack for \$3.40. Should the shopper buy 4 six-packs or 6 four-packs? Explain your reasoning.
Problem 7 (from Unit 2, Lesson 15)
On a field trip, there are 3 chaperones for every 20 students. There are 92 people on the trip. Answer these questions. If you get stuck, consider using a tape diagram.
- How many chaperones are there?
- How many children are there?
Lesson 16
Problem 1
A sign in front of a roller coaster says "You must be 40 inches tall to ride." What percentage of this height is:
- 34 inches?
- 54 inches?
Problem 2
At a hardware store, a tool set normally costs \$80. During a sale this week, the tool set costs \$12 less than usual. What percentage of the usual price is the savings? Explain or show your reasoning.
Problem 3
A bathtub can hold 80 gallons of water. The faucet flows at a rate of 4 gallons per minute. What percentage of the tub will be filled after 6 minutes?
Problem 4 (from Unit 3, Lesson 15)
The sale price of every item in a store is 85% of its usual price.
- The usual price of a backpack is \$30, what is its sale price?
- The usual price of a sweatshirt is \$18, what is its sale price?
- The usual price of a soccer ball is \$24.80, what is its sale price?
Problem 5 (from Unit 3, Lesson 9)
A shopper needs 48 hot dogs. The store sells identical hot dogs in 2 differently sized packages. They sell a six-pack of hot dogs for \$2.10, and an eight-pack of hot dogs for \$3.12. Should the shopper buy 8 six-packs, or 6 eight-packs? Explain your reasoning.
Problem 6 (from Unit 3, Lesson 4)
Elena is 56 inches tall.
-
What is her height in centimeters? (Note: 100 inches = 254 centimeters)
-
What is her height in meters?
Lesson 17
No practice problems for this lesson.