11.1: Multiplying Fractions
Evaluate each expression.
- $\frac 23 \boldcdot 27$
- $\frac 12 \boldcdot \frac 23$
- $\frac 29 \boldcdot \frac 35$
- $\frac {27}{100} \boldcdot \frac {200}{9}$
- $\left( 1\frac 34 \right) \boldcdot \frac 57$
Let’s divide fractions using the rule we learned.
Evaluate each expression.
Work with a partner. One person should work on the questions labeled “Partner A,” and the other should work on those labeled “Partner B.”
Partner A.
Find the value of each expression, and answer the question by completing the diagram that has been started for you. Show your reasoning.
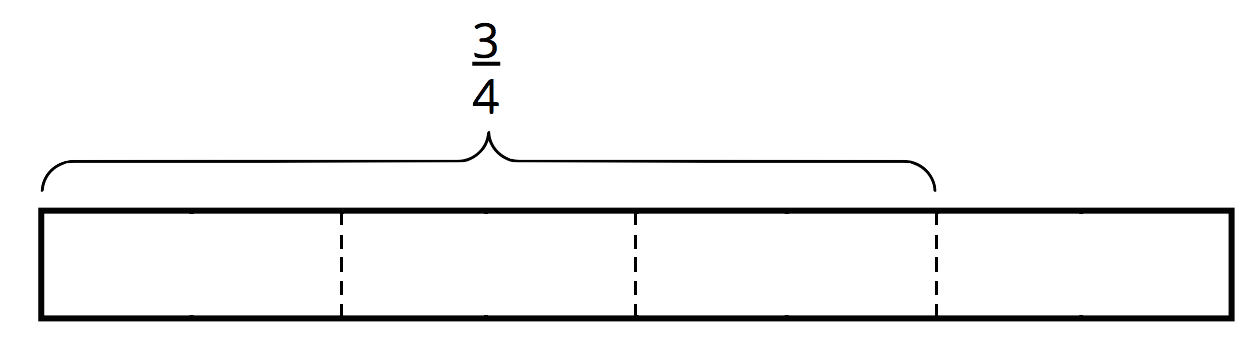
$\frac 34 \div \frac 18$
How many $\frac 18$s in $\frac 34$?
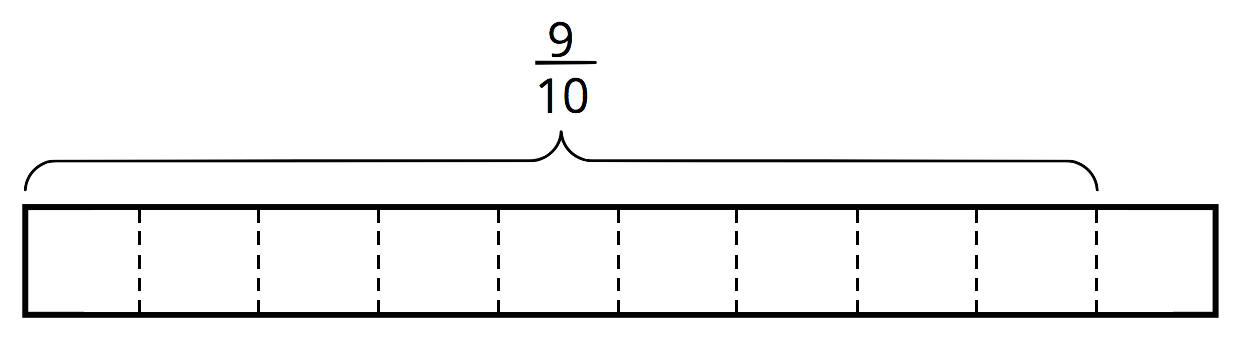
$\frac {9}{10} \div \frac 35$
How many $\frac 35$s in $\frac{9}{10}$?
Use the applet to confirm your answers and explore your own examples.
Partner B.
Elena said: “If you want to divide 4 by $\frac 25$, you can multiply 4 by 5, then divide it by 2 or multiply it by $\frac 12$.”
Find the value of each expression using the strategy that Elena described.
$\frac 34 \div \frac 18$
$\frac{9}{10} \div \frac35$
Pause here for a discussion with your partner.
Complete this statement based on your observations:
To divide a number $n$ by a fraction $\frac {a}{b}$, we can multiply $n$ by ________ and then divide the product by ________.
Select all equations that represent the statement you completed.
Calculate each quotient using your preferred strategy. Show your work and be prepared to explain your strategy.
$\frac 89 \div 4$
$\frac92 \div \frac 38$
The division $a \div \frac34 = {?}$ is equivalent to $\frac 34 \boldcdot {?} = a$, so we can think of it as meaning “$\frac34$ of what number is $a$?” and represent it with a diagram as shown. The length of the entire diagram represents the unknown number.
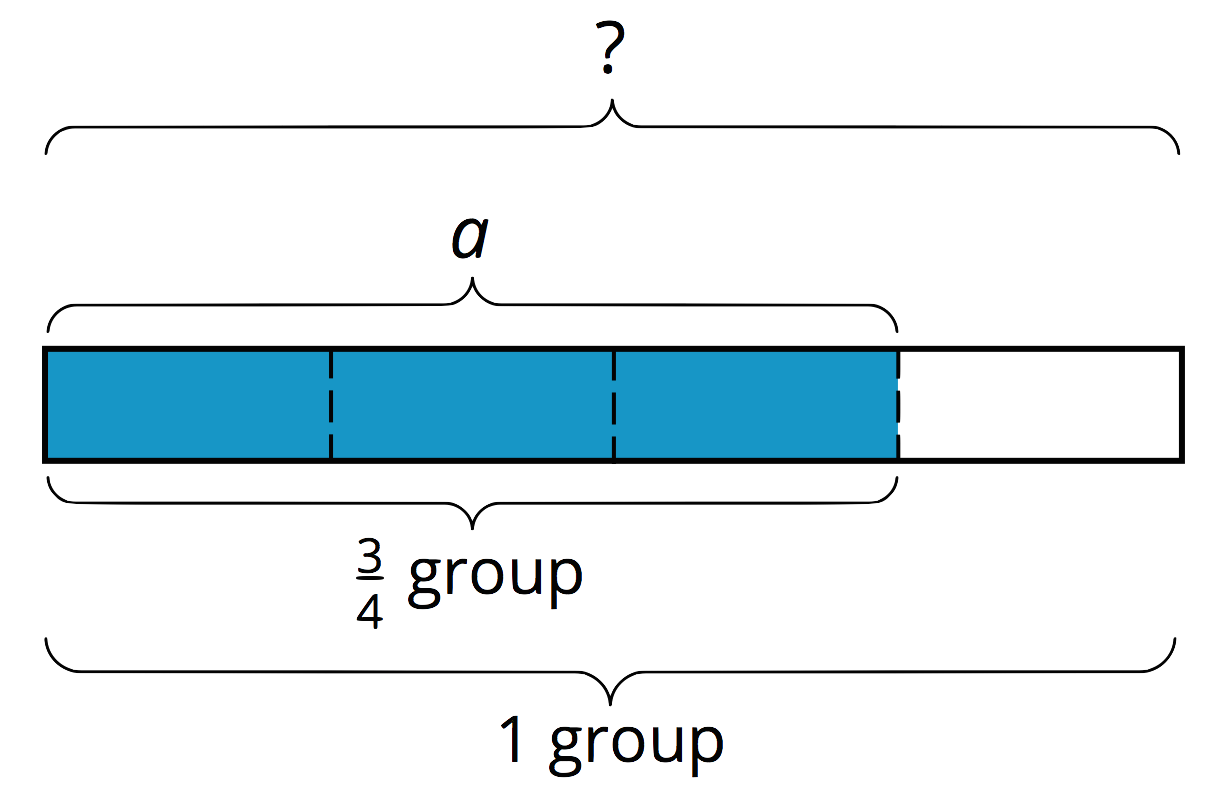
If $\frac34$ of a number is $a$, then to find the number, we can first divide $a$ by 3 to find $\frac14$ of the number. Then we multiply the result by 4 to find the number.
The steps above can be written as: $a \div 3 \boldcdot 4$. Dividing by 3 is the same as multiplying by $\frac13$, so we can also write the steps as: $a \boldcdot \frac13 \boldcdot 4$.
In other words: $a \div 3 \boldcdot 4= a \boldcdot \frac13 \boldcdot 4$. And $a \boldcdot \frac13 \boldcdot 4 = a \boldcdot \frac43$, so we can say that: $$a \div \frac34= a \boldcdot \frac43$$
In general, dividing a number by a fraction $\frac{c}{d}$ is the same as multiplying the number by $\frac{d}{c}$, which is the reciprocal of the fraction.