14.1: Area of Triangle
Find the area of Triangle A in square centimeters. Show your reasoning.
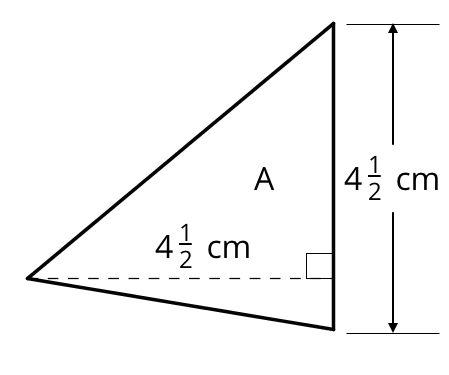
Let’s explore area and volume when fractions are involved.
Find the area of Triangle A in square centimeters. Show your reasoning.
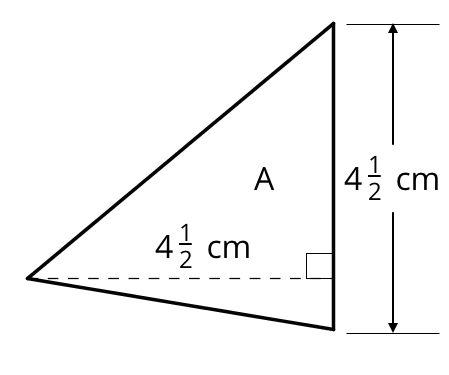
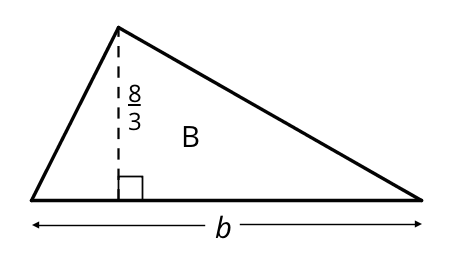

Use the cubes or the applet for the following questions.
Your teacher will give you a set of cubes with an edge length of $\frac12$ inch. Use them to help you answer the following questions.
Here is a drawing of a cube with an edge length of 1 inch. How many cubes with an edge length of $\frac12$ inch are needed to fill this cube?

Four cubes are piled in a single stack to make a prism. Each cube has an edge length of $\frac12$ inch. Sketch the prism, and find its volume in cubic inches.
Use cubes with an edge length of $\frac12$ inch to build prisms with the lengths, widths, and heights shown in the table.
For each prism, record in the table how many $\frac12$-inch cubes can be packed into the prism and the volume of the prism.
| prism length (in) |
prism width (in) |
prism height (in) |
number of $\frac12$-inch cubes in prism |
volume of prism (cu in) |
|
|---|---|---|---|---|---|
| row 1 | $\frac12$ | $\frac12$ | $\frac12$ | ||
| row 2 | 1 | 1 | $\frac12$ | ||
| row 3 | 2 | 1 | $\frac12$ | ||
| row 4 | 2 | 2 | 1 | ||
| row 5 | 4 | 2 | $\frac32$ | ||
| row 6 | 5 | 4 | 2 | ||
| row 7 | 5 | 4 | $2\frac12$ |
A unit fraction has a 1 in the numerator. These are unit fractions: $\frac13, \frac{1}{100}, \frac11$. These are not unit fractions: $\frac29, \frac81, 2\frac15$.
If a rectangular prism has edge lengths of 2 units, 3 units, and 5 units, we can think of it as 2 layers of unit cubes, with each layer having $(3 \boldcdot 5)$ unit cubes in it. So the volume, in cubic units, is: $$2\boldcdot 3\boldcdot 5$$
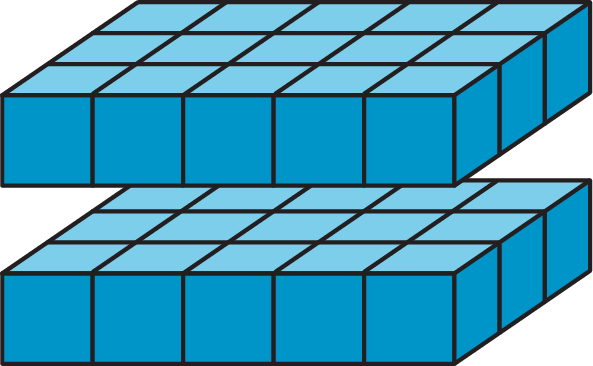
To find the volume of a rectangular prism with fractional edge lengths, we can think of it as being built of cubes that have a unit fraction for their edge length. For instance, if we build a prism that is $\frac12$-inch tall, $\frac32$-inch wide, and 4 inches long using cubes with a $\frac12$-inch edge length, we would have:
The volume of the prism would be $1 \boldcdot 3 \boldcdot 8$, or 24 cubic units. How do we find its volume in cubic inches?
We know that each cube with a $\frac12$-inch edge length has a volume of $\frac 18$ cubic inch, because $\frac 12 \boldcdot \frac 12 \boldcdot \frac 12 = \frac18$. Since the prism is built using 24 of these cubes, its volume, in cubic inches, would then be $24 \boldcdot \frac 18$, or 3 cubic inches.
The volume of the prism, in cubic inches, can also be found by multiplying the fractional edge lengths in inches: $$ \frac 12 \boldcdot \frac 32 \boldcdot 4 = 3$$