2.1: A Division Expression
Here is an expression: $20\div 4$.
What are some ways to think about this expression? Describe at least two meanings you think it could have.
Lesson 2: Meanings of Division
Let’s explore ways to think about division.
2.2: Bags of Almonds
A baker has 12 pounds of almonds. She puts them in bags, so that each bag has the same weight.
- Clare and Tyler drew diagrams and wrote equations to show how they were thinking about $12 \div 6$.
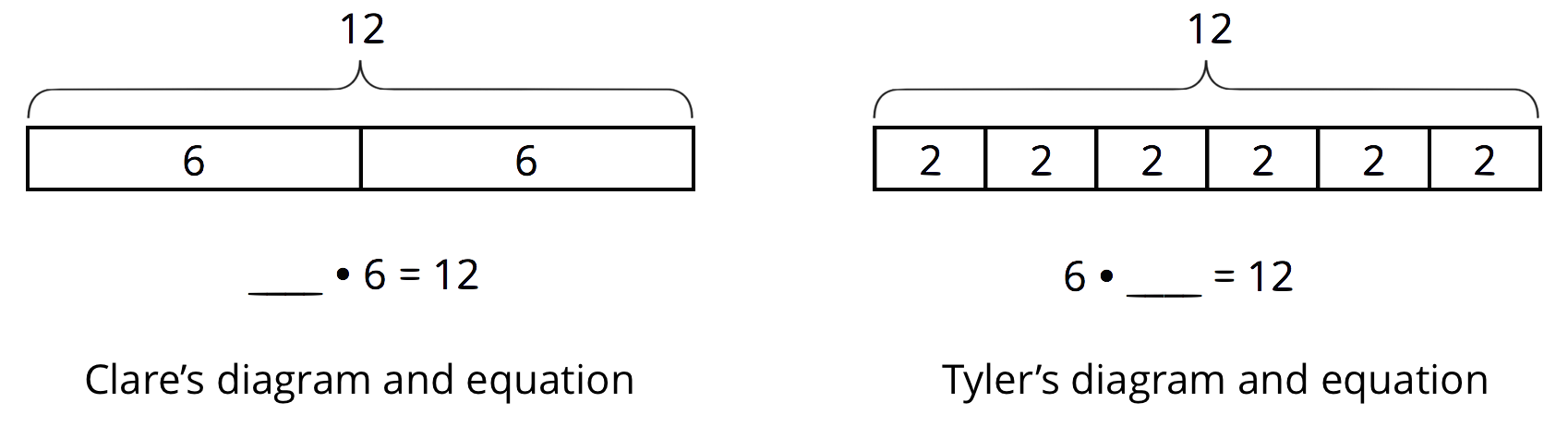
How do you think Clare and Tyler thought about $12 \div 6$? Explain what each diagram and each part of each equation (especially the missing number) might mean in the context of the bags of almonds.
Pause here for a class discussion. -
Explain what each division expression could mean in the context of the bags of almonds. Then draw a diagram and write a multiplication equation to show how you are thinking about the expression.
- $12 \div 4$
- $12 \div 2$
- $12 \div \frac12$
A loaf of bread is cut into slices.
- If each slice is $\frac12$ of a loaf, how many slices are there?
- If each slice is $\frac15$ of a loaf, how many slices are there?
- What happens to the number of slices as each slice gets smaller?
- Interpret the meaning of dividing by 0 in the context of slicing bread.
Summary
Suppose 24 bagels are being distributed into boxes. The expression $24 \div 3$ could be understood in two ways:
- 24 bagels are distributed equally into 3 boxes, as represented by this diagram:
- 24 bagels are distributed into boxes, 3 bagels in each box, as represented by this diagram:
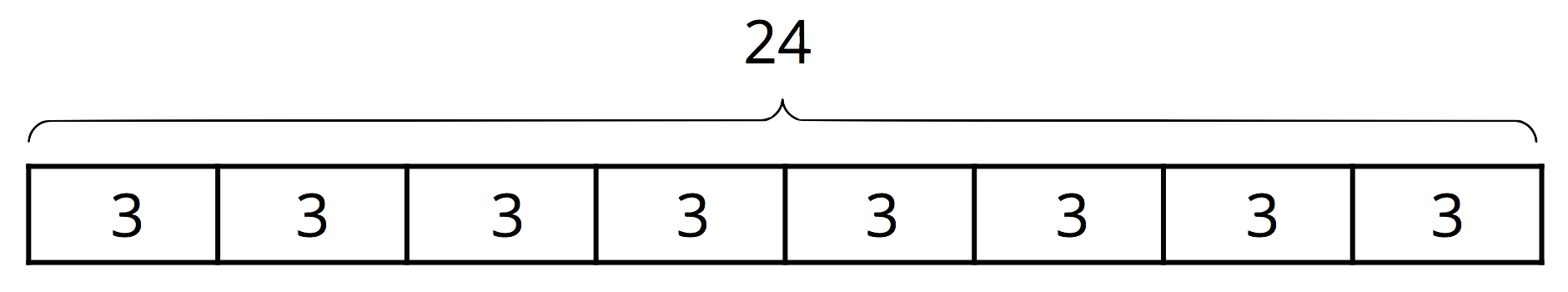
In both interpretations, the quotient is the same ($24 \div 3 = 8$), but it has different meanings in each case. In the first case, the 8 represents the number of bagels in each of the 3 boxes. In the second, it represents the number of boxes that were formed with 3 bagels in each box.
These two ways of seeing division are related to how 3, 8, and 24 are related in a multiplication. Both $3 \boldcdot 8$ and $8 \boldcdot 3$ equal 24.
- $3 \boldcdot 8 =24$ can be read as “3 groups of 8 make 24.”
- $8 \boldcdot 3 = 24$ can be read as “8 groups of 3 make 24.”
If 3 and 24 are the only numbers given, the multiplication equations would be: $$3 \boldcdot {?} =24$$ $${?} \boldcdot 3 =24$$
In both cases, the division $24 \div 3$ can be used to find the value of the “?” But now we see that it can be interpreted in more than one way, because the “?” can refer to the size of a group (as in “3 groups of what number make 24?”), or to the number of groups (as in “How many groups of 3 make 24?”).