Suppose one batch of cookies requires $\frac23$ cup flour. How many batches can be made with 4 cups of flour?
We can think of the question as being: “How many $\frac23$ are in 4?” and represent it using multiplication and division equations.
$${?} \boldcdot \frac23 = 4$$ $$4\div \frac23 = {?}$$
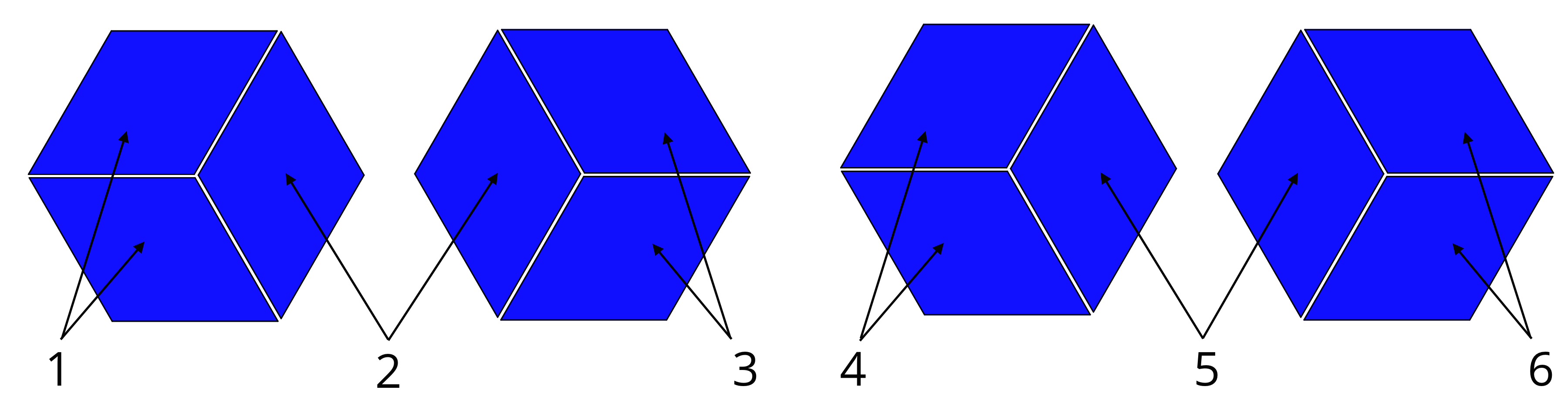
Let’s use pattern blocks to visualize the situation and say that a hexagon is 1 whole.
Since 3 rhombuses make a hexagon, 1 rhombus represents $\frac13$ and 2 rhombuses represent $\frac 23$. We can see that 6 pairs of rhombuses make 4 hexagons, so there are 6 groups of $\frac 23$ in 4.
Other kinds of diagrams can also help us reason about equal-sized groups involving fractions. This example shows how we might reason about the same question from above: “How many $\frac 23$-cups are in 4 cups?”
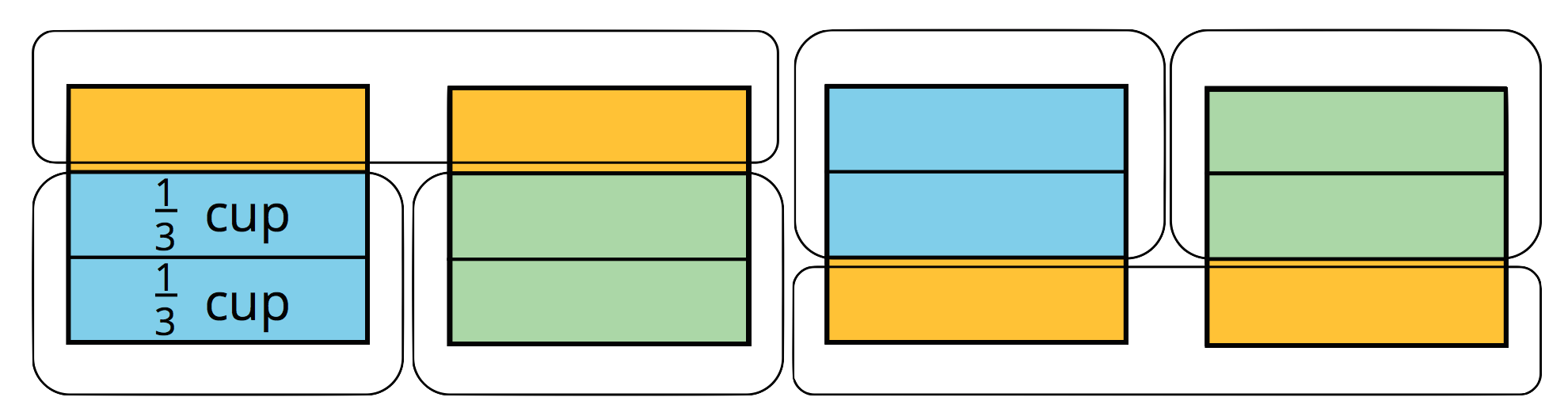
We can see each “cup” partitioned into thirds, and that there are 6 groups of $\frac23$-cup in 4 cups. In both diagrams, we see that the unknown value (or the “?” in the equations) is 6. So we can now write:
$$6 \boldcdot \frac23 = 4$$ $$4\div \frac23 = 6$$