A baker used 2 kilograms of flour to make several batches of a pastry recipe. The recipe called for $\frac25$ kilogram of flour per batch. How many batches did she make?
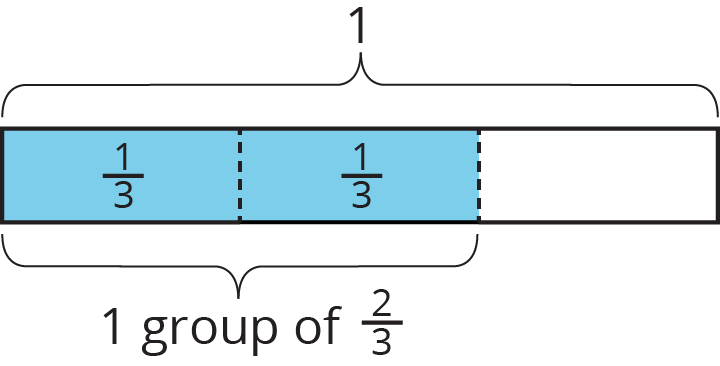
We can think of the question as: “How many groups of $\frac25$ kilogram make 2 kilograms?” and represent that question with the equations:
$${?} \boldcdot \frac25=2$$ $$2 \div \frac25 = {?}$$
To help us make sense of the question, we can draw a tape diagram. This diagram shows 2 whole kilograms, with each kilogram partitioned into fifths.
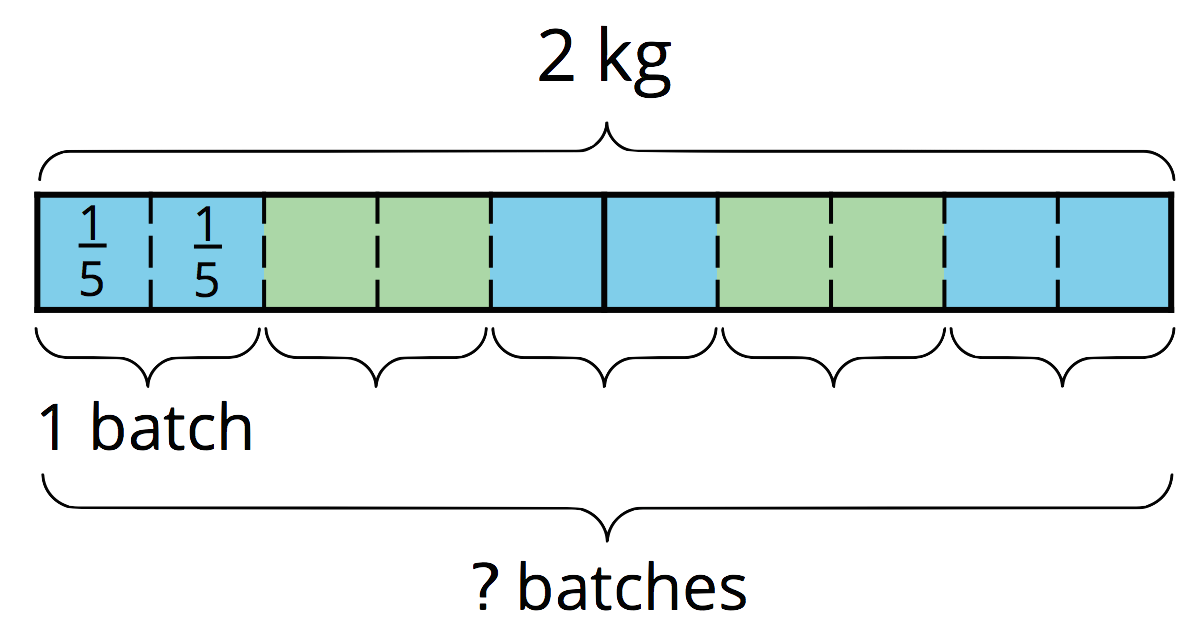
We can see there are 5 groups of $\frac 25$ in 2. Multiplying 5 and $\frac25$ allows us to check this answer: $5 \boldcdot \frac 25 = \frac{10}{5}$ and $\frac {10}{5} = 2$, so the answer is correct.
Notice the number of groups that result from $2 \div \frac25$ is a whole number. Sometimes the number of groups we find from dividing may not be a whole number. Here is an example:
Suppose one serving of rice is $\frac34$ cup. How many servings are there in $3\frac12$ cups?
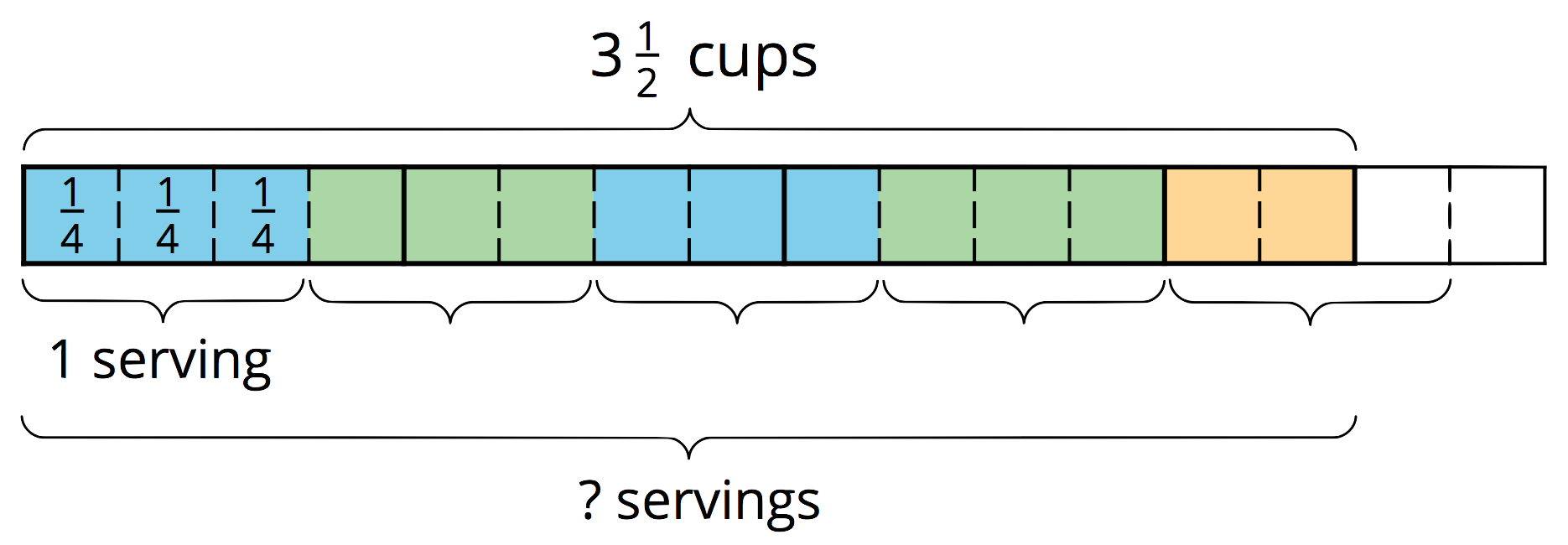
$${?}\boldcdot \frac34 = 3\frac12$$ $$3\frac12 \div \frac34 = {?}$$
Looking at the diagram, we can see there are 4 full groups of $\frac 34$, plus 2 fourths. If 3 fourths make a whole group, then 2 fourths make $\frac 23$ of a group. So the number of servings (the “?” in each equation) is $4\frac23$. We can check this by multiplying $4\frac23$ and $\frac34$.
$4\frac23 \boldcdot \frac34 = \frac{14}{3} \boldcdot \frac34$, and $\frac{14}{3} \boldcdot \frac34 = \frac{14}{4}$, which is indeed equivalent to $3\frac12$.