a. If the 5 represents the number of people, what does the 4 represent?
Unit 4: Practice Problem Sets
Lesson 1
Problem 1
Order from smallest to largest:
- Number of pennies in a stack that is 1 ft high
- Number of books in a stack that is 1 ft high
- Number of dollar bills in a stack that is 1 ft high
- Number of slices of bread in a stack that is 1 ft high
Problem 2
Use each of the numbers 4, 40, and 4000 once to make true statements.
-
The value of $\underline{\hspace{1in}} \div 40.01$ is close to 1
-
The value of $\underline{\hspace{1in}} \div 40.01$ is much less than 1.
-
The value of $ \underline{\hspace{1in}}\div 40.01$ is much greater than 1.
Problem 3
Without computing, decide whether the value of each expression is much smaller than 1, close to 1, or much greater than 1.
- $100 \div \frac{1}{1000}$
- $50\frac13 \div 50\frac14$
- $4.7 \div 5.2$
- $2 \div 7335$
- $2,\!000,\!001 \div 9$
- $0.002 \div 2,\!000$
Problem 4 (from Unit 3, Lesson 16)
A rocking horse has a weight limit of 60 pounds.
- What percentage of the weight limit is 33 pounds?
- What percentage of the weight limit is 114 pounds?
-
What weight is 95% of the limit?
Problem 5 (from Unit 3, Lesson 15)
Compare using $>$, $=$, or $<$.
-
0.7 ______ 0.70
-
$0.03 + \frac{6}{10}$ ______ $0.30 + \frac{6}{100}$
-
0.9 ______ 0.12
Problem 6 (from Unit 3, Lesson 14)
Diego has 90 songs on his playlist. How many songs are there for each genre?
- 40% rock
- 10% country
- 30% hip-hop
- The rest is electronica
Problem 7 (from Unit 3, Lesson 8)
A garden hose emits 9 quarts of water in 6 seconds. At this rate:
- How long will it take the hose to emit 12 quarts?
- How much water does the hose emit in 10 seconds?
Lesson 2
Problem 1
Twenty pounds of strawberries are being shared equally by a group of friends. The equation $20 \div 5=4$ represents the division of strawberries.
b. If the 5 represents the pounds of strawberries per person, what does the 4 represent?
Problem 2
A sixth-grade science club needs \$180 to pay for the tickets to a science museum. All tickets cost the same amount.
What could $180 \div 15$ mean in this context? Describe two interpretations of the expression. Then, find the quotient and explain what it means in each interpretation.
Problem 3
Write a multiplication equation that corresponds to each division equation.
a. $ 10 \div 5 = {?} $
b. $ 4.5 \div 3 = {?} $
c. $ \frac12 \div 4 = {?} $
Problem 4
Write a division or multiplication equation that represents each situation. Use a “?” for the unknown quantity.
- 2.5 gallons of water are poured into 5 equally sized bottles. How much water is in each bottle?
- A large bucket of 200 golf balls is divided into 4 smaller buckets. How many golf balls are in each small bucket?
-
Sixteen socks are put into pairs. How many pairs are there?
Problem 5 (from Unit 4, Lesson 1)
Find a value for $a$ that makes each statement true.
- $a\div6$ is greater than 1
- $a\div6$ is equal to 1
- $a\div6$ is less than 1
- $a\div6$ is equal to a whole number
Problem 6 (from Unit 3, Lesson 14)
Complete the table. Write each percentage as a percent of 1.
| fraction | decimal | percentage | |
|---|---|---|---|
| row 1 | \(\frac14\) | 0.25 | 25% of 1 |
| row 2 | 0.1 | ||
| row 3 | 75% of 1 | ||
| row 4 | \(\frac15\) | ||
| row 5 | 1.5 | ||
| row 6 | 140% of 1 |
Problem 7 (from Unit 3, Lesson 8)
Jada walks at a speed of 3 miles per hour. Elena walks at a speed of 2.8 miles per hour. If they both begin walking along a walking trail at the same time, how much farther will Jada walk after 3 hours? Explain your reasoning.
Lesson 3
Problem 1
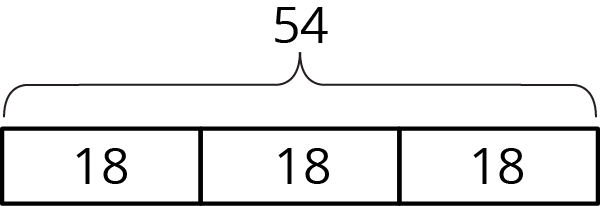
Problem 2
Mai has \$36 to spend on movie tickets. Each movie ticket costs \$4.50. How many tickets can she buy?
- Write a multiplication equation and a division equation to represent this situation.
- Find the answer. Draw a diagram, if needed.
- Use the multiplication equation to check your answer.
Problem 3
Kiran said that this diagram can show the solution to $16\div 8 = {?}$ or $16 \div 2={?}$, depending on how we think about the equations and the “?”.
Explain or show how Kiran is correct.

Problem 4 (from Unit 4, Lesson 2)
Problem 5 (from Unit 4, Lesson 1)
Noah said, “When you divide a number by a second number, the result will always be smaller than the first number.”
Jada said, “I think the result could be larger or smaller, depending on the numbers.”
Do you agree with Noah or Jada? Show or explain your reasoning.
Problem 6 (from Unit 3, Lesson 7)
Mini muffins cost \$3.00 per dozen.
- Andre says, “I have \$2.00, so I can afford 8 muffins.”
- Elena says, “I want to get 16 muffins, so I’ll need to pay \$4.00."
Do you agree with either, both, or neither of them? Explain your reasoning.
Problem 7 (from Unit 3, Lesson 15)
A family has a monthly budget of \$2,400. How much money is spent on each category?
- 44% is spent on housing.
- 23% is spent on food.
- 6% is spent on clothing.
- 17% is spent on transportation.
- The rest is put into savings.
Lesson 4
Problem 1
A shopper buys cat food in bags of 3 lbs. Her cat eats $\frac34$ lb each week. How many weeks does one bag last?
-
Draw a diagram to represent the situation and label your diagram so it can be followed by others. Answer the question.
-
Write a multiplication or division equation to represent the situation.
-
Multiply your answer in the first question (the number of weeks) by $\frac34$. Did you get 3 as a result? If not, revise your previous work.
Problem 2
Use the diagram to answer the question: How many $\frac13$s are in $1\frac23$? The hexagon represents 1 whole. Explain or show your reasoning.

Problem 3
Which question can be represented by the equation ${?}\boldcdot \frac18=3$?
- How many 3s are in $\frac18$?
- What is 3 groups of $\frac18$?
- How many $\frac 18$s are in 3?
- What is $\frac 18$ of 3?
Problem 4
Write two division equations for each multiplication equation.
- $15\boldcdot \frac25 = 6$
- $6 \boldcdot \frac43 = 8$
- $16\boldcdot \frac78 = 14$
Problem 5 (from Unit 4, Lesson 2)
Noah and his friends are going to an amusement park. The total cost of admission for 8 students is \$100, and all students share the cost equally. Noah brought \$13 for his ticket. Did he bring enough money to get into the park? Explain your reasoning.
Problem 6 (from Unit 4, Lesson 1)
Write a division expression with a quotient that is:
- greater than $8 \div 0.001$
- less than $8 \div 0.001$
- between $8 \div 0.001$ and $8 \div \frac{1}{10}$
Problem 7 (from Unit 3, Lesson 14)
Find each unknown number.
- 12 is 150% of what number?
- 5 is 50% of what number?
- 10% of what number is 300?
- 5% of what number is 72?
- 20 is 80% of what number?
Lesson 5
Problem 1
Use the tape diagram to represent and find the value of $\frac12\div\frac13$.
Mark up and label the diagram as needed.
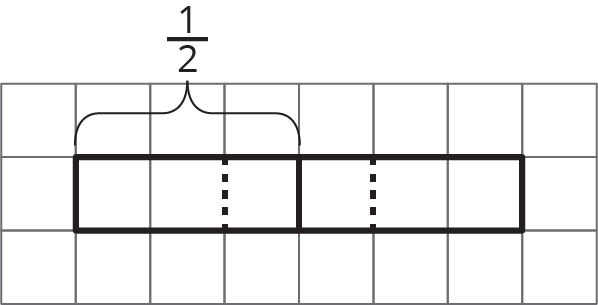
Problem 2
What is the value of $\frac12\div\frac13$? Use pattern blocks to represent and find this value. The yellow hexagon represents 1 whole. Explain or show your reasoning.

Problem 3
Use a standard inch ruler to answer each question. Then, write a multiplication equation and a division equation that answer the question.
-
How many $\frac12$s are in 7?
-
How many $\frac38$s are in 6?
-
How many $\frac{5}{16}$s are in $1\frac78$?
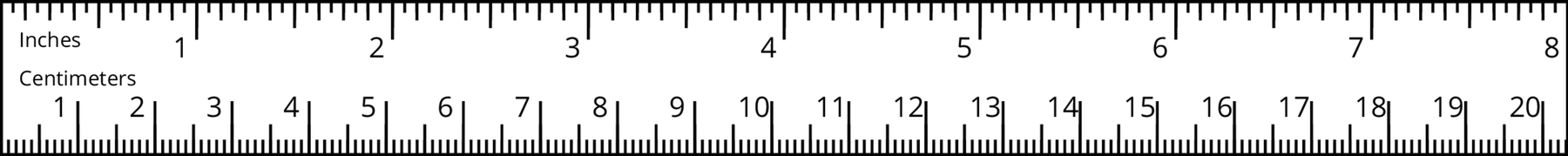
Problem 4
Use the tape diagram to represent and answer the question: How many $\frac25$s are in $1\frac12$?
Mark up and label the diagram as needed.

Problem 5 (from Unit 4, Lesson 4)
Write a multiplication equation and a division equation to represent each question, statement, or diagram.
- There are 12 fourths in 3.
-
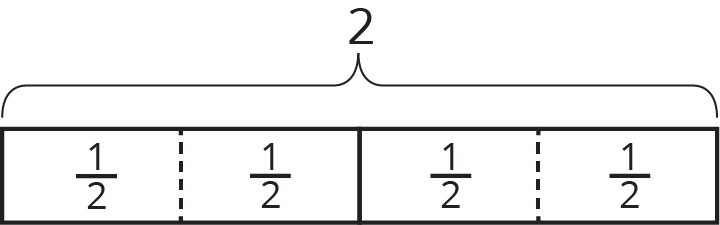
- How many $\frac 23$s are in 6?
-
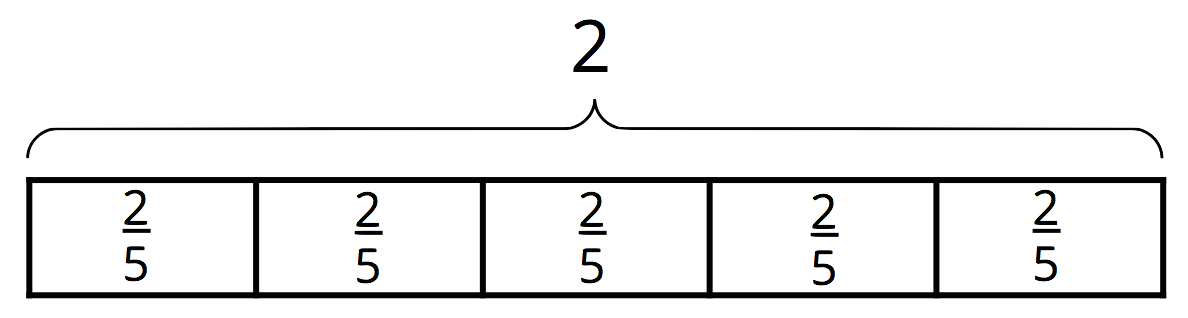
Problem 6 (from Unit 3, Lesson 5)
At a farmer’s market, two vendors sell fresh milk. One vendor sells 2 liters for \$3.80, and another vendor sells 1.5 liters for \$2.70. Which is the better deal? Explain your reasoning.
Problem 7 (from Unit 3, Lesson 6)
A recipe uses 5 cups of flour for every 2 cups of sugar.
- How much sugar is used for 1 cup of flour?
- How much flour is used for 1 cup of sugar?
- How much flour is used with 7 cups of sugar?
- How much sugar is used with 6 cups of flour?
Lesson 6
Problem 1
We can think of $3\div \frac14$ as the answer to the question “How many groups of $\frac14$ are in 3?” Draw a tape diagram to represent the question. Then answer the question.
Problem 2
Describe how to draw a tape diagram to represent and answer $3 \div \frac35 = {?}$ for a friend who was absent.
Problem 3
How many groups of $\frac12$ days are in 1 week?
- Write a multiplication equation or a division equation to represent the question.
- Draw a tape diagram to show the relationship between the quantities and to answer the question. Use graph paper, if needed.
Problem 4
Problem 5 (from Unit 4, Lesson 5)
Select all equations that can represent the question: “How many groups of $\frac45$ are in 1?”
- ${?} \boldcdot 1=\frac45$
- $1 \boldcdot \frac45 = {?}$
- $\frac45 \div 1 = {?}$
- ${?} \boldcdot \frac45 =1$
- $1\div \frac45 = {?}$
Problem 6 (from Unit 3, Lesson 14)
Calculate each percentage mentally.
- What is 10% of 70?
- What is 10% of 110?
- What is 25% of 160?
- What is 25% of 48?
- What is 50% of 90?
- What is 50% of 350?
- What is 75% of 300?
- What is 75% if 48?
Lesson 7
Problem 1
A recipe calls for $\frac12$ lb of flour for 1 batch. How many batches can be made with each of the following amounts?
- 1 lb
- $\frac34$ lb
- $\frac14$ lb
Problem 2
Whiskers the cat weighs $2\frac23$ kg. Piglio weighs $4$ kg. For each question, write a multiplication and a division equation, decide whether the answer is greater or less than 1, and then answer the question.
- How many times as heavy as Piglio is Whiskers?
- How many times as heavy as Whiskers is Piglio?
Problem 3
Andre is walking from home to a festival that is $1\frac58$ kilometers away. He takes a quick rest after walking $\frac13$ kilometers. In this situation, which question can be represented by the equation: ${?} \boldcdot 1\frac58 = \frac13$?
- What fraction of the trip has Andre completed?
- How many more kilometers does he have to walk to get to the festival?
- What fraction of the trip is left?
- How many kilometers is it from home to the festival and back home?
Problem 4
Draw a tape diagram to represent and answer the question: What fraction of $2\frac12$ is $\frac45$?
Problem 5 (from Unit 4, Lesson 6)
How many groups of $\frac34$ are in each of the following quantities?
- $\frac{11}{4}$
- $6\frac12$
Problem 6 (from Unit 4, Lesson 4)
Which question can be represented by the equation $4\div \frac27 = {?}$
- What is 4 groups of $\frac 27$?
- How many $\frac27$s are in 4?
- What is $\frac 27$ of 4?
- How many 4s are in $\frac27$?
Lesson 8
Problem 1
For each scenario, use the given tape diagram to help you answer the question. Mark up and label the diagrams as needed.
-
Mai has picked 1 cup of strawberries for a cake, which is enough for $\frac34$ of the cake. How many cups does she need for the whole cake?

-
Priya has picked $1\frac12$ cups of raspberries, which is enough for $\frac34$ of a cake. How many cups does she need for the whole cake?

Problem 2
Tyler painted $ \frac92$ square yards of wall area with 3 gallons of paint. How many gallons of paint does it take to paint each square yard of wall?
-
Write multiplication and division equations to represent the situation.
- Draw a diagram to represent the situation and to answer the question.
Problem 3
After walking $\frac 14$ mile from home, Han is $\frac 13$ of his way to school. What is the distance between his home and school?
-
Write multiplication and division equations to represent this situation.
-
Use the given diagram to help you answer the question. Mark up and label it as needed.

Problem 4 (from Unit 4, Lesson 7)
Here is a division equation: $\frac45 \div \frac23 = {?}$
- Write a multiplication equation that corresponds to the division equation.
-
Draw a diagram to represent and answer the question.
Problem 5 (from Unit 4, Lesson 3)
A set of books that are each 1.5 inches wide are being organized on a bookshelf that is 36 inches wide. How many books can fit on the shelf?
- Write a multiplication equation and a division equation to represent this question.
- Find the answer. Draw a diagram, if needed.
- Use the multiplication equation to check your answer.
Problem 6 (from Unit 4, Lesson 1)
- Without calculating, order the expressions based on their values, from smallest to largest.
$56\div8$
$56\div8,\!000,\!000$
$56\div 0.000008$
- Explain how you decided the order of the three expressions.
- Find a number $n$ so that $56\div n$ is greater than 1 but less than 7.
Lesson 9
Problem 1
A group of friends is sharing $2\frac12$ pounds of berries.
- If each friend received $\frac54$ of a pound of berries, how many friends are sharing the berries?
- If 5 friends are sharing the berries, how many pounds of berries does each friend receive?
Problem 2
$\frac25$ kilogram of soil fills $\frac13$ of a container. Can 1 kilogram of soil fit in the container? Explain or show your reasoning.
Problem 3
After raining for $\frac34$ of an hour, a rain gauge is $\frac25$ filled. If it continues to rain at that rate for 15 more minutes, what fraction of the rain gauge will be filled?
- To help answer this question, Diego wrote the division equation $\frac34\div \frac25={?}$. Explain why this equation does not represent the situation.
- Write a multiplication equation and a division equation that does represent the situation.

Problem 4 (from Unit 2, Lesson 8)
3 tickets to the museum cost \$12.75. At this rate, what is the cost of:
- 1 ticket?
- 5 tickets?
Problem 5 (from Unit 2, Lesson 9)
Elena went 60 meters in 15 seconds. Noah went 50 meters in 10 seconds. Elena and Noah both moved at a constant speed.
- How far did Elena go in 1 second?
- How far did Noah go in 1 second?
-
Who went faster? Explain or show your reasoning.
Problem 6 (from Unit 2, Lesson 11)
The first row in the table shows a recipe for 1 batch of trail mix. Complete the remaining rows with recipes for 2, 3, and 4 batches of the same type of trail mix.
| number of batches | cups of cereal | cups of almonds | cups of raisins | |
|---|---|---|---|---|
| row 1 | 1 | 2 | $\frac13$ | $\frac14$ |
| row 2 | 2 | |||
| row 3 | 3 | |||
| row 4 | 4 |
Lesson 10
Problem 1
Priya is sharing 24 apples equally with some friends. She uses division to determine how many people can have a share if each person gets a particular number of apples. For example, $24 \div 4 = 6$ means that if each person gets 4 apples, 6 people can have apples. Here are some other calculations:
$24 \div 4 = 6$
$24 \div 2 = 12$
$24 \div 1 = 24$
$24 \div \frac12 = {?}$
-
Priya thinks the “?” represents a number less than 24. Do you agree? Explain or show your reasoning.
- In the case of $24 \div \frac12 = {?}$, how many people can have apples?
Problem 2
Here is a centimeter ruler.

- Use the ruler to find $1 \div \frac{1}{10}$ and $4 \div \frac{1}{10}$.
- What calculation did you do each time?
-
Use your work from the first part to find each quotient.
- $18 \div \frac{1}{10}$
- $4\div \frac{2}{10}$
- $4\div \frac{8}{10}$
Problem 3
Find each quotient.
a. $5 \div \frac{1}{10}$
b. $5 \div \frac{3}{10}$
c. $5\div \frac{9}{10}$
Problem 4
Use the fact that $2\frac12 \div \frac18=20$ to find $2\frac12 \div \frac58$. Explain or show your reasoning.
Problem 5 (from Unit 4, Lesson 9)
It takes one week for a crew of workers to pave $\frac35$ kilometer of a road. At that rate, how long will it take to pave 1 kilometer?
Write a multiplication equation and a division equation that represent the question and then answer the question. Show your reasoning.
Problem 6 (from Unit 4, Lesson 7)
A box contains $1\frac 34$ pounds of pancake mix. Jada used $\frac 78$ pound for a recipe. What fraction of the pancake mix in the box did she use? Explain or show your reasoning. Draw a diagram, if needed.
Problem 7 (from Unit 3, Lesson 14)
Calculate each percentage mentally.
- 25% of 400
- 50% of 90
- 75% of 200
- 10% of 8,000
- 5% of 20
Lesson 11
Problem 1
Select all statements that show correct reasoning for finding $\frac{14}{15}\div \frac{7}{5}$.
- Multiplying $\frac{14}{15}$ by 5 and then by $\frac{1}{7}$.
- Dividing $\frac{14}{15}$ by 5, and then multiplying by $\frac{1}{7}$.
- Multiplying $\frac{14}{15}$ by 7, and then multiplying by $\frac{1}{5}$.
- Multiplying $\frac{14}{15}$ by 5 and then dividing by 7.
Problem 2
Clare said that $\frac{4}{3}\div\frac52$ is $\frac{10}{3}$. She reasoned: $\frac{4}{3} \boldcdot 5=\frac{20}{3}$ and $\frac{20}{3}\div 2=\frac{10}{3}$.
Explain why Clare’s answer and reasoning are incorrect. Find the correct quotient.
Problem 3
Find the value of $\frac{15}{4}\div \frac{5}{8}$. Show your reasoning.
Problem 4
Kiran has $2\frac34$ pounds of flour. When he divides the flour into equal-sized bags, he fills $4\frac18$ bags. How many pounds fit in each bag?
Problem 5 (from Unit 4, Lesson 10)
Divide $4\frac12$ by the following unit fractions.
a. $\frac18$
b. $\frac14$
c. $\frac16$
Problem 6 (from Unit 4, Lesson 9)
After charging for $\frac13$ of an hour, a phone is at $\frac25$ of its full power. How long will it take the phone to charge completely?
Decide whether each equation can represent the situation.
- $\frac13\boldcdot {?}=\frac25$
- $\frac13\div \frac25={?}$
- $\frac25 \div \frac13 ={?}$
- $\frac25 \boldcdot {?}=\frac13$
Problem 7 (from Unit 4, Lesson 8)
Elena and Noah are each filling a bucket with water. Noah’s bucket is $\frac25$ full and the water weighs $2\frac12$ pounds. How much does Elena’s bucket weigh if her bucket is full and her bucket is identical to Noah’s?
- Write multiplication and division equations to represent the question.
- Draw a diagram to show the relationship between the quantities and to answer the question.
Lesson 12
Problem 1
One inch is around $2\frac{11}{20}$ centimeters.

- How many centimeters long is 3 inches? Show your reasoning.
- What fraction of an inch is 1 centimeter? Show your reasoning.
- What question can be answered by finding $10 \div 2\frac{11}{20}$?
Problem 2
A zookeeper is $6\frac14$ feet tall. A young giraffe in his care is $9\frac38$ feet tall.
- How many times as tall as the zookeeper is the giraffe?
- What fraction of the giraffe’s height is the zookeeper’s height?
Problem 3
A rectangular bathroom floor is covered with square tiles that are $1\frac12$ feet by $1\frac12$ feet. The length of the bathroom floor is $10\frac12$ feet and the width is $6\frac12$ feet.
- How many tiles does it take to cover the length of the floor?
- How many tiles does it take to cover the width of the floor?
Problem 4 (from Unit 4, Lesson 11)
The Food and Drug Administration (FDA) recommends a certain amount of nutrient intake per day called the “daily value.” Food labels usually show percentages of the daily values for several different nutrients—calcium, iron, vitamins, etc.
In $\frac34$ cup of oatmeal, there is $\frac{1}{10}$ of the recommended daily value of iron. What fraction of the daily recommended value of iron is in 1 cup of oatmeal?
Write a multiplication equation and a division equation to represent the question, and then answer the question. Show your reasoning.
Problem 5 (from Unit 4, Lesson 7)
What fraction of $\frac12$ is $\frac13$? Draw a tape diagram to represent and answer the question. Use graph paper if needed.
Problem 6 (from Unit 4, Lesson 6)
Noah says, “There are $2\frac12$ groups of $\frac45$ in 2.” Do you agree with his statement? Draw a tape diagram to show your reasoning. Use graph paper, if needed.
Lesson 13
Problem 1
- Find the unknown side length of the rectangle if its area is 11 m2. Show your reasoning.
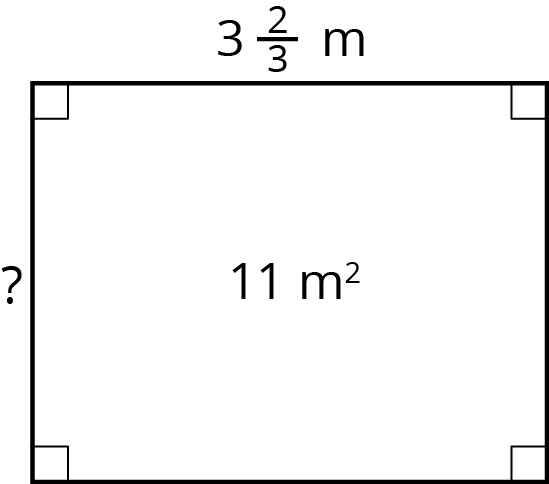
- Check your answer by multiplying it by the given side length ($3\frac 23$). Is the resulting product 11? If not, revisit your work for the first question.
Problem 2
A worker is tiling the floor of a rectangular room that is 12 feet by 15 feet. The tiles are square with side lengths $1\frac13$ feet. How many tiles are needed to cover the entire floor? Show your reasoning.
Problem 3
A television screen has length $16\frac12$ inches, width $w$ inches, and area 462 square inches. Select all equations that represent the relationship of the side lengths and area of the television.
- $w \boldcdot 462 = 16\frac12$
- $16\frac12 \boldcdot w = 462$
- $462 \div 16\frac12 = w$
- $462 \div w= 16\frac12$
- $16\frac12 \boldcdot 462 = w$
Problem 4
The area of a rectangle is $17\frac12$ in2 and its shorter side is $3\frac12$ in. Draw a diagram that shows this information. What is the length of the longer side?
Problem 5 (from Unit 4, Lesson 12)
A bookshelf is 42 inches long.
- How many books of length $1\frac12$ inches will fit on the bookshelf? Explain your reasoning.
- A bookcase has 5 of these bookshelves. How many feet of shelf space is there? Explain your reasoning.
Problem 6 (from Unit 4, Lesson 11)
Find the value of $\frac{5}{32}\div \frac{25}{4}$. Show your reasoning.
Problem 7 (from Unit 4, Lesson 6)
How many groups of $1\frac23$ are in each of the following quantities?
a. $1\frac56$
b. $4\frac13$
c. $\frac56$
Problem 8 (from Unit 2, Lesson 14)
It takes $1\frac{1}{4}$ minutes to fill a 3-gallon bucket of water with a hose. At this rate, how long does it take to fill a 50-gallon tub? If you get stuck, consider using the table.
Lesson 14
Problem 1
Clare is using little wooden cubes with edge length $\frac12$ inch to build a larger cube that has edge length 4 inches. How many little cubes does she need? Explain your reasoning.
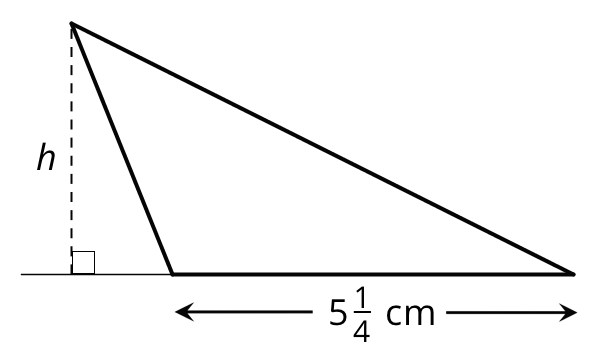
Problem 2
The triangle has an area of $7\frac{7}{8}$ cm2 and a base of $5\frac14$ cm.
What is the length of $h$? Explain your reasoning.
Problem 3
-
Which of the following expressions can be used to find how many cubes with edge length of $\frac13$ unit fit in a prism that is 5 units by 5 units by 8 units? Explain or show your reasoning.
-
$(5 \boldcdot \frac 13) \boldcdot (5 \boldcdot \frac 13) \boldcdot (8 \boldcdot \frac 13)$
-
$5 \boldcdot 5 \boldcdot 8$
-
$(5 \boldcdot 3) \boldcdot (5 \boldcdot 3) \boldcdot (8 \boldcdot 3)$
-
$(5 \boldcdot 5 \boldcdot 8) \boldcdot (\frac 13)$
-
-
Mai says that we can also find the answer by multiplying the edge lengths of the prism and then multiplying the result by 27. Do you agree with her statement? Explain your reasoning.
Problem 4 (from Unit 4, Lesson 12)
A builder is building a fence with $6\frac14$-inch-wide wooden boards, arranged side-by-side with no gaps. How many boards are needed to build a fence that is 150 inches long? Show your reasoning.
Problem 5 (from Unit 4, Lesson 12)
Find the value of each expression. Show your reasoning and check your answer.
- $2\frac17 \div \frac27$
- $\frac {17}{20} \div \frac14$
Problem 6 (from Unit 4, Lesson 11)
A bucket contains $11\frac23$ gallons of water and is $\frac56$ full. How many gallons of water would be in a full bucket?
Write a multiplication and a division equation to represent the situation, and then find the answer. Show your reasoning.
Problem 7 (from Unit 3, Lesson 12)
There are 80 kids in a gym. 75% are wearing socks. How many are not wearing socks? If you get stuck, consider using a tape diagram showing sections that each represent 25% of the kids in the gym.
Problem 8 (from Unit 3, Lesson 11)
- Lin wants to save \$75 for a trip to the city. If she has saved \$37.50 so far, what percentage of her goal has she saved? What percentage remains?
- Noah wants to save \$60 so that he can purchase a concert ticket. If he has saved \$45 so far, what percentage of his goal has he saved? What percentage remains?
Lesson 15
Problem 1
A pool in the shape of a rectangular prism is being filled with water. The length and width of the pool is 24 feet and 15 feet. If the height of the water in the pool is $1\frac13$ feet, what is the volume of the water in cubic feet?
Problem 2
A rectangular prism measures $2\frac25$ inches by $3\frac15$ inches by 2 inch.
- Priya said, “It takes more cubes with edge length$\frac25$ inch than cubes with edge length $\frac15$ inch to pack the prism.” Do you agree with Priya’s statement? Explain or show your reasoning.
-
How many cubes with edge length $\frac15$ inch fit in the prism? Show your reasoning.
- Explain how you can use your answer in the previous question to find the volume of the prism in cubic inches.
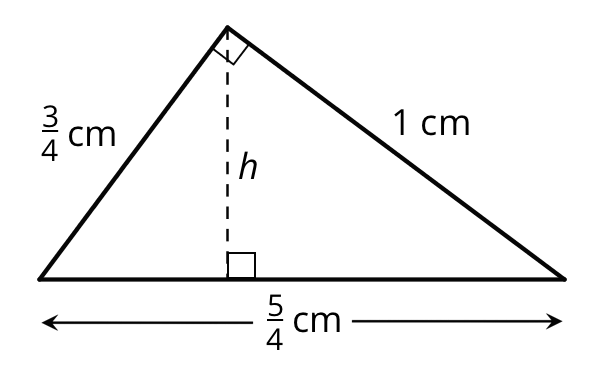
Problem 3 (from Unit 4, Lesson 14)
- Here is a right triangle. What is its area?
-
What is the height $h$ for the base that is $\frac54$ units long? Show your reasoning.
Problem 4
To give their animals essential minerals and nutrients, farmers and ranchers often have a block of salt—called “salt lick”—available for their animals to lick.
-
A rancher is ordering a box of cube-shaped salt licks. The edge lengths of each salt lick are $\frac{5}{12}$ foot. Is the volume of one salt lick greater or less than 1 cubic foot? Explain your reasoning.

- The box that contains the salt lick is $1\frac14$ feet by $1\frac23$ feet by $\frac56$ feet. How many cubes of salt lick fit in the box? Explain or show your reasoning.
Problem 5 (from Unit 4, Lesson 12)
- How many groups of $\frac13$ inch are in $\frac34$ inch?
- How many inches are in $1\frac25$ groups of $1\frac23$ inches?
Problem 6 (from Unit 2, Lesson 12)
Here is a table that shows the ratio of flour to water in an art paste. Complete the table with values in equivalent ratios.
| cups of flour | cups of water | |
|---|---|---|
| row 1 | 1 | $\frac12$ |
| row 2 | 4 | |
| row 3 | 3 | |
| row 4 | $\frac12$ |
Lesson 16
Problem 1
An orange has about $\frac14$ cup of juice. How many oranges are needed to make $2\frac12$ cups of juice? Select all equations that represent this question.
- $ {?} \boldcdot \frac 14= 2\frac12$
- $\frac14 \div 2\frac12 = {?}$
- ${?} \boldcdot 2\frac12 = \frac14$
- $2\frac12 \div \frac14 = {?}$
Problem 2
Mai, Clare, and Tyler are hiking from a parking lot to the summit of a mountain. They pass a sign that gives distances.
- Parking lot: $\frac34$ mile
- Summit: $1\frac12$ miles
Mai says: “We are one third of the way there.” Clare says: “We have to go twice as far as we have already gone.” Tyler says: “The total hike is three times as long as what we have already gone.”
Can they all be correct? Explain how you know.
Problem 3
Priya’s cat weighs $5\frac12$ pounds and her dog weighs $8\frac14$ pounds. Estimate the missing number in each statement before calculating the answer. Then, compare your answer to the estimate and explain any discrepancy.
-
The cat is _______ as heavy as the dog.
-
Their combined weight is _______ pounds.
-
The dog is _______ pounds heavier than the cat.
Problem 4 (from Unit 4, Lesson 15)
Before refrigerators existed, some people had blocks of ice delivered to their homes. A delivery wagon had a storage box in the shape of a rectangular prism that was $7\frac12$ feet by 6 feet by 6 feet. The cubic ice blocks stored in the box had side lengths $1\frac12$ feet. How many ice blocks fit in the storage box?
- 270
- $3\frac38$
- 80
- 180
Problem 5 (from Unit 4, Lesson 1)
Fill in the blanks with 0.001, 0.1, 10, or 1000 so that the value of each quotient is in the correct column.
close to $\frac{1}{100}$
- ____ $ \div 9$
- $12 \div$ ____
close to 1
- ____ $\div 0.12$
- $\frac18 \div$ ____
greater than 100
- ____ $\div \frac13$
- $700.7 \div$ ____
Problem 6 (from Unit 3, Lesson 15)
A school club sold 300 shirts. 31% were sold to fifth graders, 52% were sold to sixth graders, and the rest were sold to teachers. How many shirts were sold to each group—fifth graders, sixth graders, and teachers? Explain or show your reasoning.
Problem 7 (from Unit 2, Lesson 15)
- From the information given above, can you determine how many coins Jada has?
- If Jada has 55 coins, how many of each kind of coin does she have?
- How much are her coins worth?
Lesson 17
No practice problems for this lesson.