10.1: Number Talk: Estimating Quotients
Estimate these quotients mentally.
$500 \div 7$
$1,\!394 \div 9$
Let’s use long division.
Estimate these quotients mentally.
$500 \div 7$
$1,\!394 \div 9$
Lin has a method of calculating quotients that is different from Elena’s method and Andre’s method. Here is how she found the quotient of $657\div 3$:
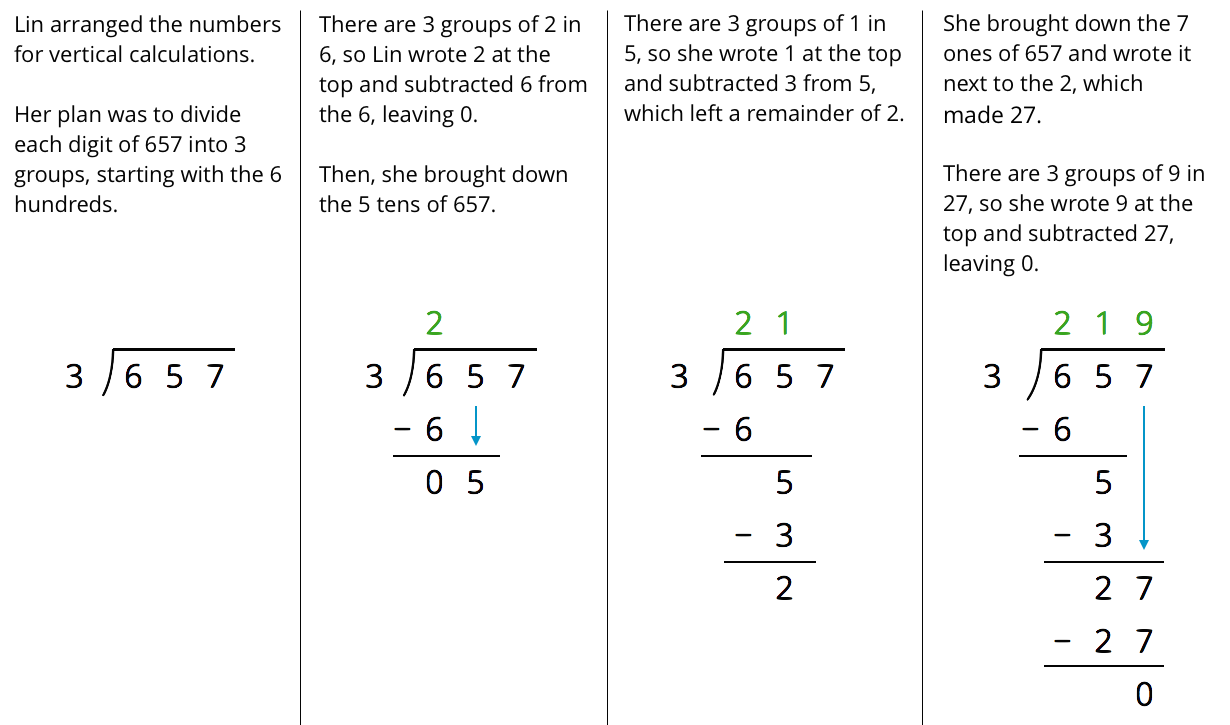
Discuss with your partner how Lin’s method is similar to and different from drawing base-ten diagrams or using the partial quotients method.
$846 \div 3$
$1,\!816 \div 4$
$768 \div 12$
Find each quotient.
Here is Priya’s calculation of $906 \div 3$.
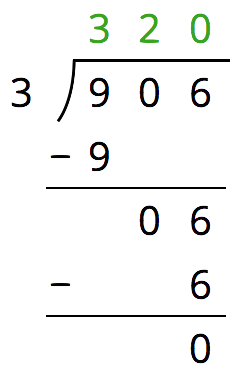
Priya wrote 320 for the value of $906 \div 3$. Check her answer by multiplying it by 3. What product do you get and what does it tell you about Priya’s answer?
Long division is another method for calculating quotients. It relies on place value to perform and record the division.
When we use long division, we work from left to right and with one digit at a time, starting with the leftmost digit of the dividend. We remove the largest group possible each time, using the placement of the digit to indicate the size of each group. Here is an example of how to find $948 \div 3$ using long division.
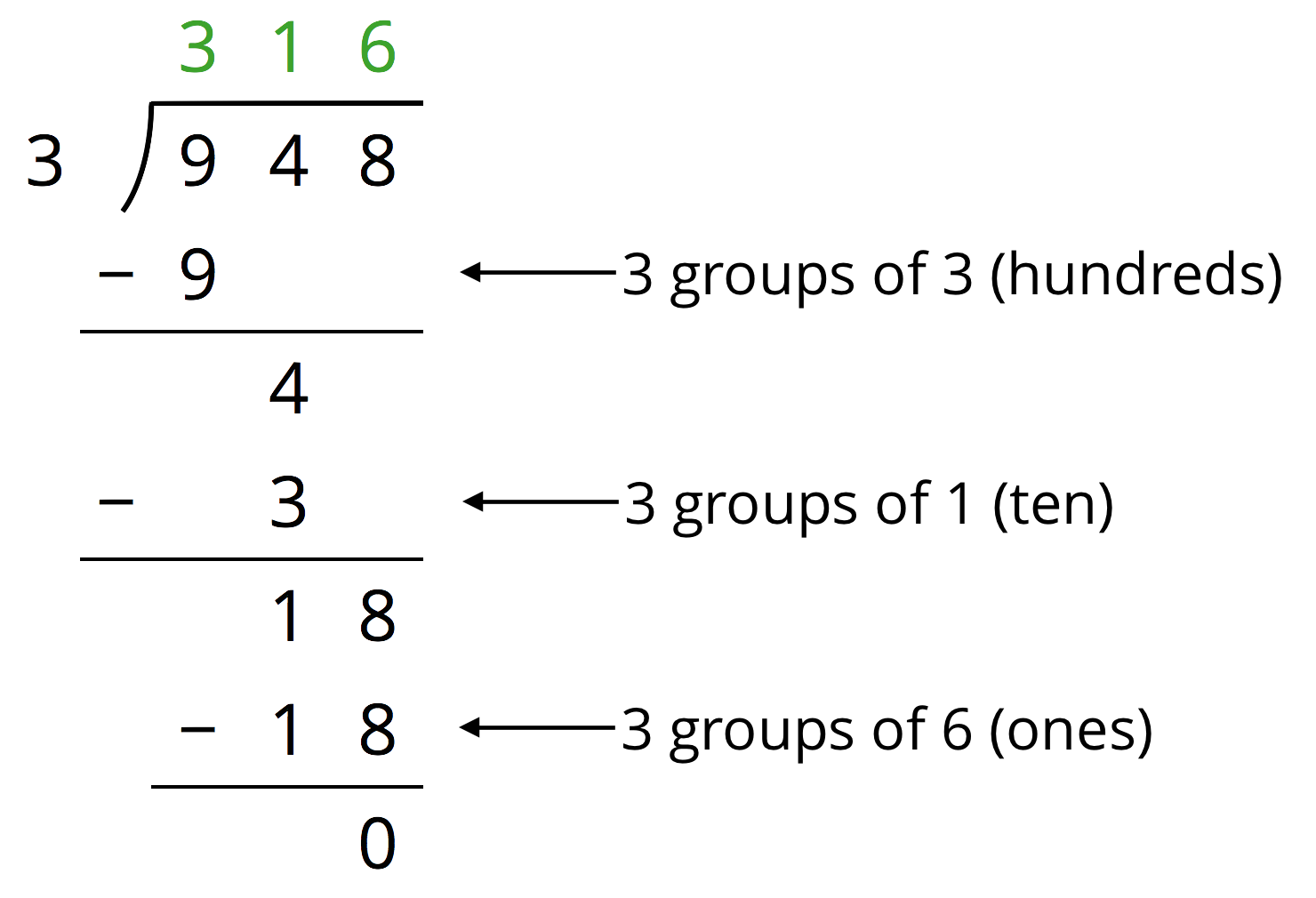
We start by dividing 9 hundreds into 3 groups, which means 3 hundreds in each group. Instead of writing 300, we simply write 3 in the hundreds place, knowing that it means 3 hundreds.
There are no remaining hundreds, so we work with the tens. We can make 3 groups of 1 ten in 4 tens, so we write 1 in the tens place above the 4 of 948. Subtracting 3 tens from 4 tens, we have a remainder of 1 ten.
We know that 1 ten is 10 ones. Combining these with the 8 ones from 948, we have 18 ones. We can make 3 groups of 6, so we write 6 in the ones place.
In total, there are 3 groups of 3 hundreds, 1 ten, and 6 ones in 948, so $948 \div 3 = 316$.
Long division is an algorithm for finding the quotient of two numbers expressed in decimal form. It works by building up the quotient one digit at a time, from left to right. Each time you get a new digit, you multiply the divisor by the corresponding base ten value and subtract that from the dividend.
Using long division we see that $513 \div 4 = 128 \frac14$. We can also write this as $513 = 128 \times 4 + 1$.
$$ \require{enclose} \begin{array}{r} 128 \\[-3pt] 4 \enclose{longdiv}{513}\kern-.2ex \\[-3pt] \underline{4{00}} \\[-3pt] 113 \\[-3pt] \underline{\phantom{0}8{0}} \\[-3pt] \phantom{0}33 \\[-3pt] \underline{\phantom{0}32} \\[-3pt] \phantom{00}1 \end{array} $$