14.1: Close Estimates
For each expression, choose the best estimate of its value.
- $76.2\div15$
- 0.5
- 5
- 50
- $56.34\div48$
- 1
- 10
- 100
- $124.3\div 20$
- 6
- 60
- 600
Let’s solve some problems using decimals.
For each expression, choose the best estimate of its value.
Your teacher will assign to you either Problem A or Problem B. Work together as a group to answer the questions. Be prepared to create a visual display to show your reasoning with the class.
Problem A: A piece of rope is 5.75 meters in length.
If it is cut into 20 equal pieces, how long will each piece be?
If it is cut into 0.05-meter pieces, how many pieces will there be?
Problem B: A tortoise travels 0.945 miles in 3.5 hours.
At this rate, how long will it take the tortoise to travel 4.86 miles?
 Tortoise
Copyright Owner:
skeeze
License:
Public Domain
Via:
Pixabay
Tortoise
Copyright Owner:
skeeze
License:
Public Domain
Via:
Pixabay
There are 10 equally-spaced hurdles on a race track. The first hurdle is 13.72 meters from the start line. The final hurdle is 14.02 meters from the finish line. The race track is 110 meters long.
 August 3rd London Olympics 2012 stadium hurdles
Copyright Owner:
Steve Flair
License:
CC BY 2.0
Via:
Wikimedia Commons
August 3rd London Olympics 2012 stadium hurdles
Copyright Owner:
Steve Flair
License:
CC BY 2.0
Via:
Wikimedia Commons
A professional runner takes 3 strides between each pair of hurdles. The runner leaves the ground 2.2 meters before the hurdle and returns to the ground 1 meter after the hurdle.
About how long are each of the runner’s strides between the hurdles? Show your reasoning.
Here is a diagram of a tennis court.
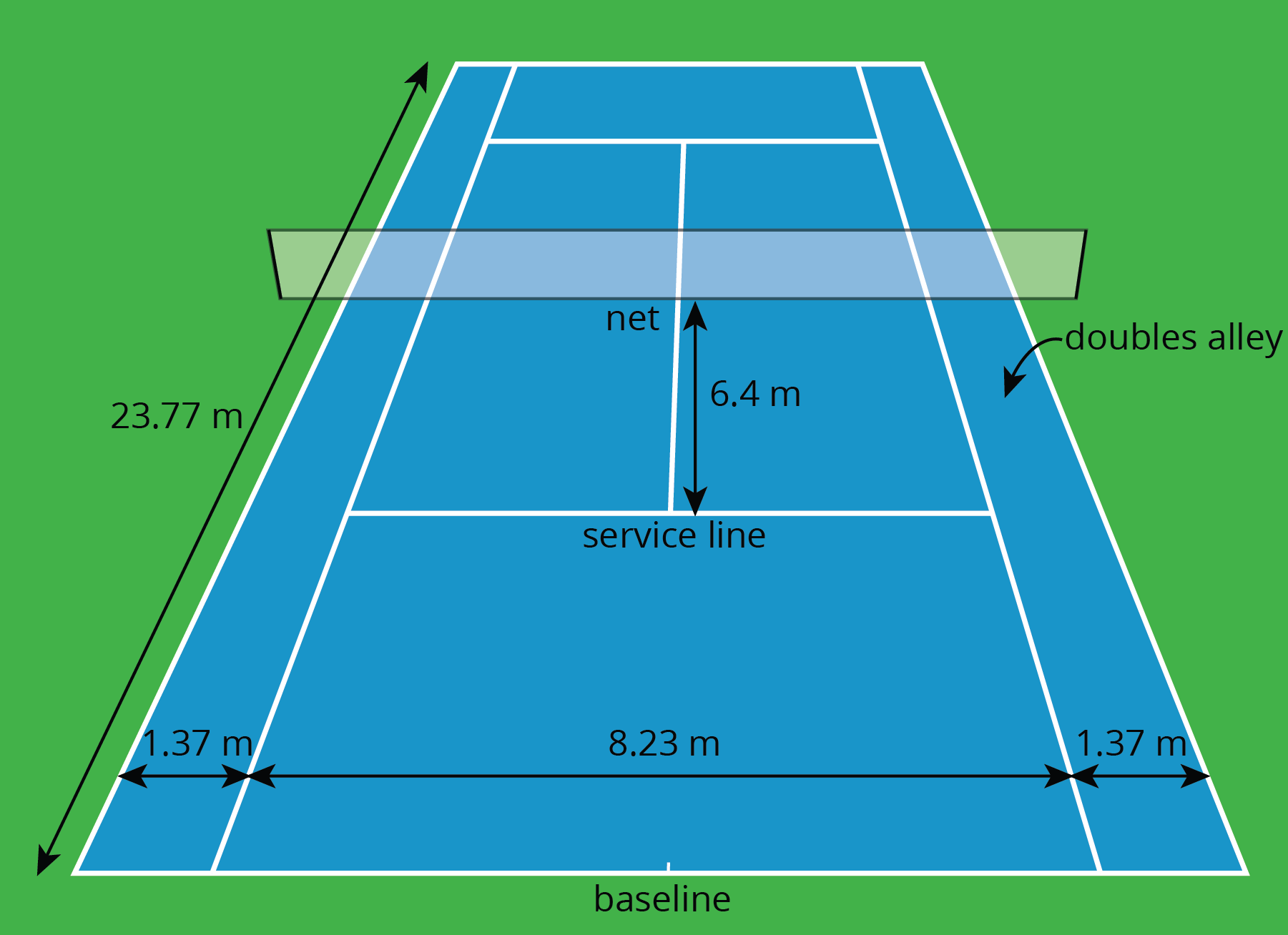
The full tennis court, used for doubles, is a rectangle. All of the angles made by the line segments in the diagram are right angles.
Lines painted on a tennis court are 5 cm wide. A painter made markings to show the length and width of the court, then painted the lines to the outside of the markings.
Diagrams can help us communicate and model mathematics. A clearly-labeled diagram helps us visualize what is happening in a problem and accurately communicate the information we need.
Sports offer great examples of how diagrams can help us solve problems. For example, to show the placement of the running hurdles in a diagram, we needed to know what the distances 13.72 and 14.02 meters tell us and the number of hurdles to draw. An accurate diagram not only helped us set up and solve the problem correctly, but also helped us see that there are only nine spaces between ten hurdles.
To communicate information clearly and solve problems correctly, it is also important to be precise in our measurements and calculations, especially when they involve decimals.
In tennis, for example, the length of the court is 23.77 meters. Because the boundary lines on a tennis court have a significant width, we would want to know whether this measurement is taken between the inside of the lines, the center of the lines, or the outside of the lines. Diagrams can help us attend to this detail, as shown here.
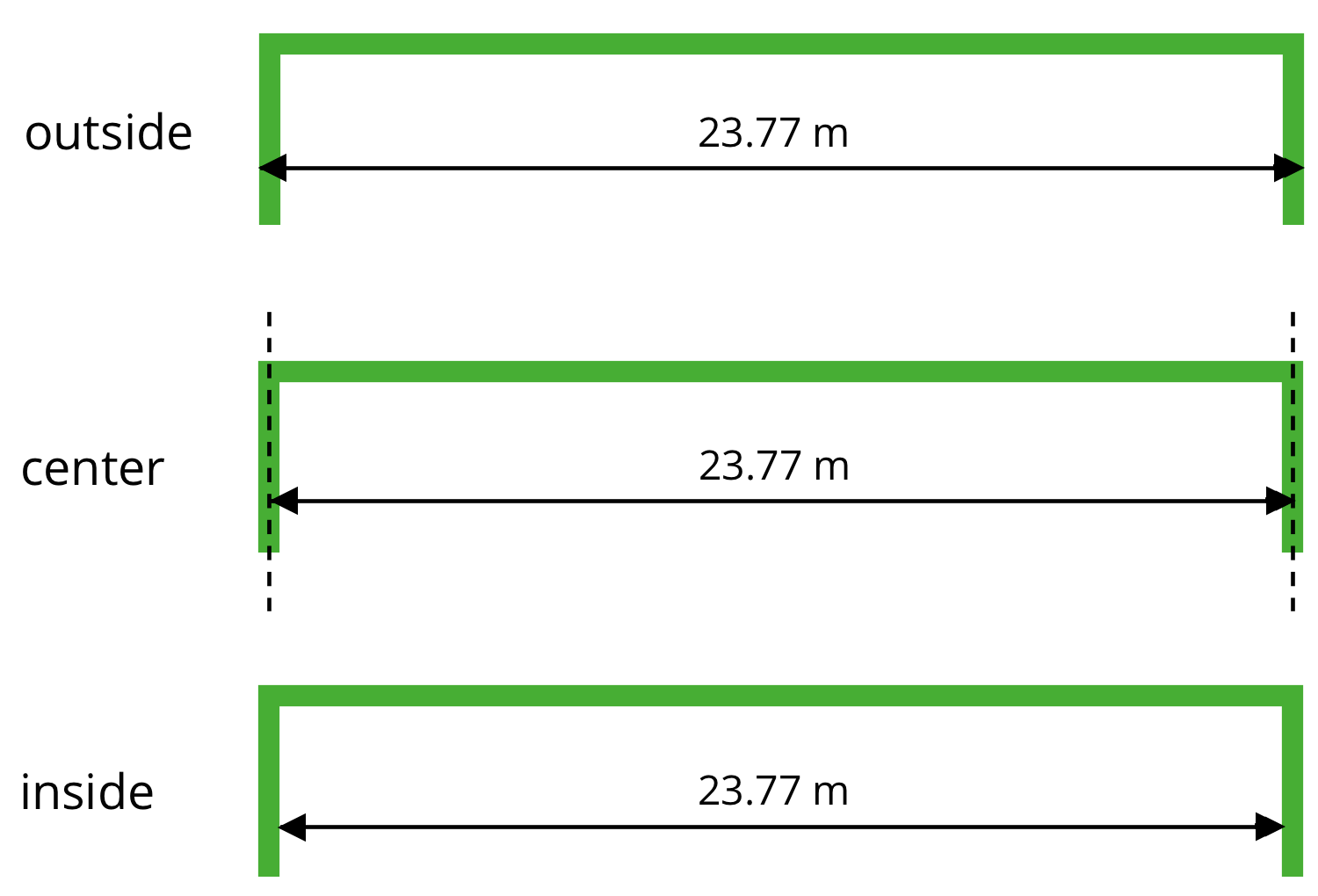
The accuracy of this measurement matters to the tennis players who use the court, so it matters to those who paint the boundaries as well. The tennis players practice their shots to be on or within certain lines. If the tennis court on which they play is not precisely measured, their shots may not land as intended in relation to the boundaries. Court painters usually need to be sure their measurements are accurate to within $\frac{1}{100}$ of a meter or one centimeter.