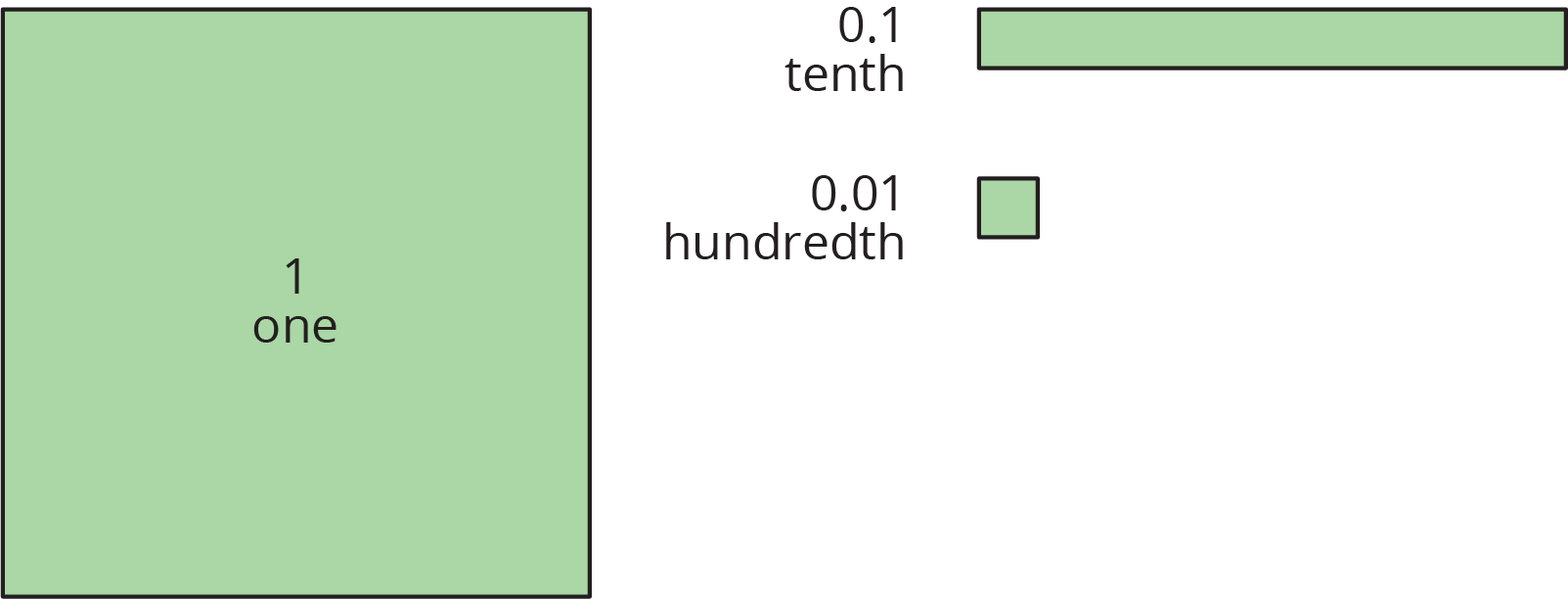
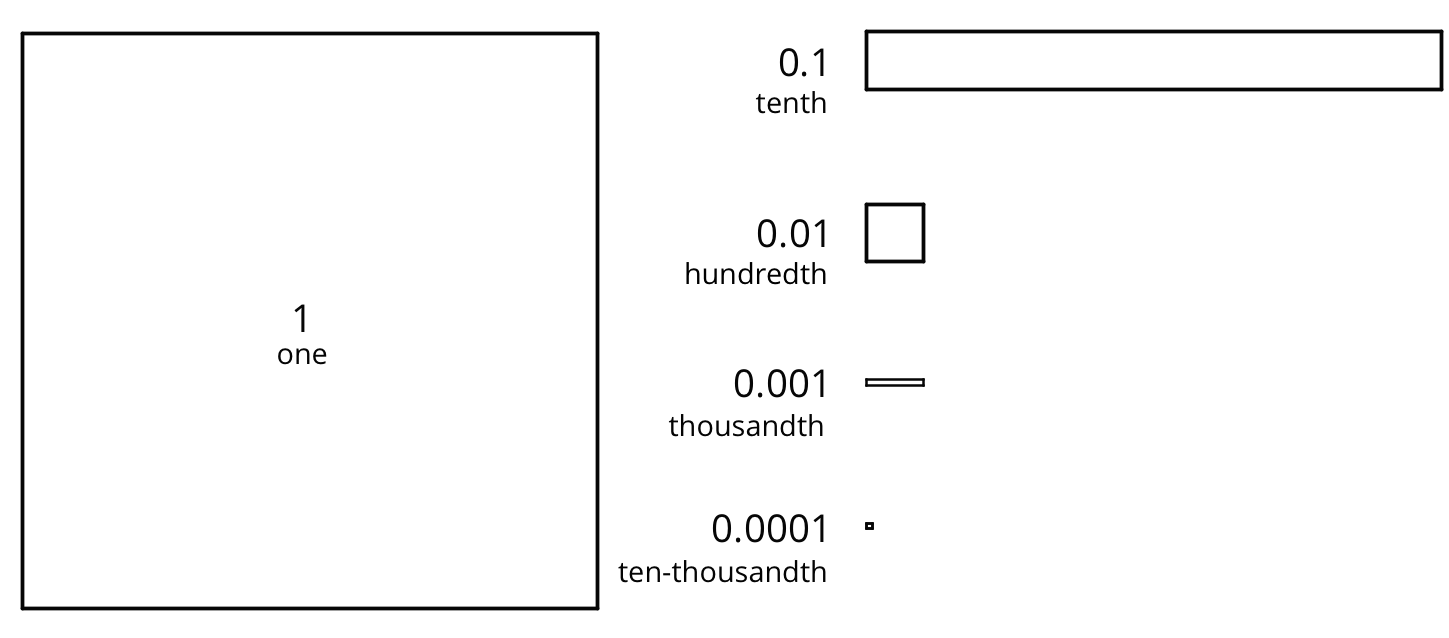
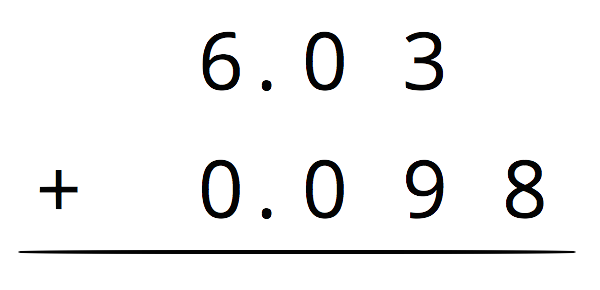Base-ten diagrams represent collections of base-ten units—tens, ones, tenths, hundredths, etc. We can use them to help us understand sums of decimals.
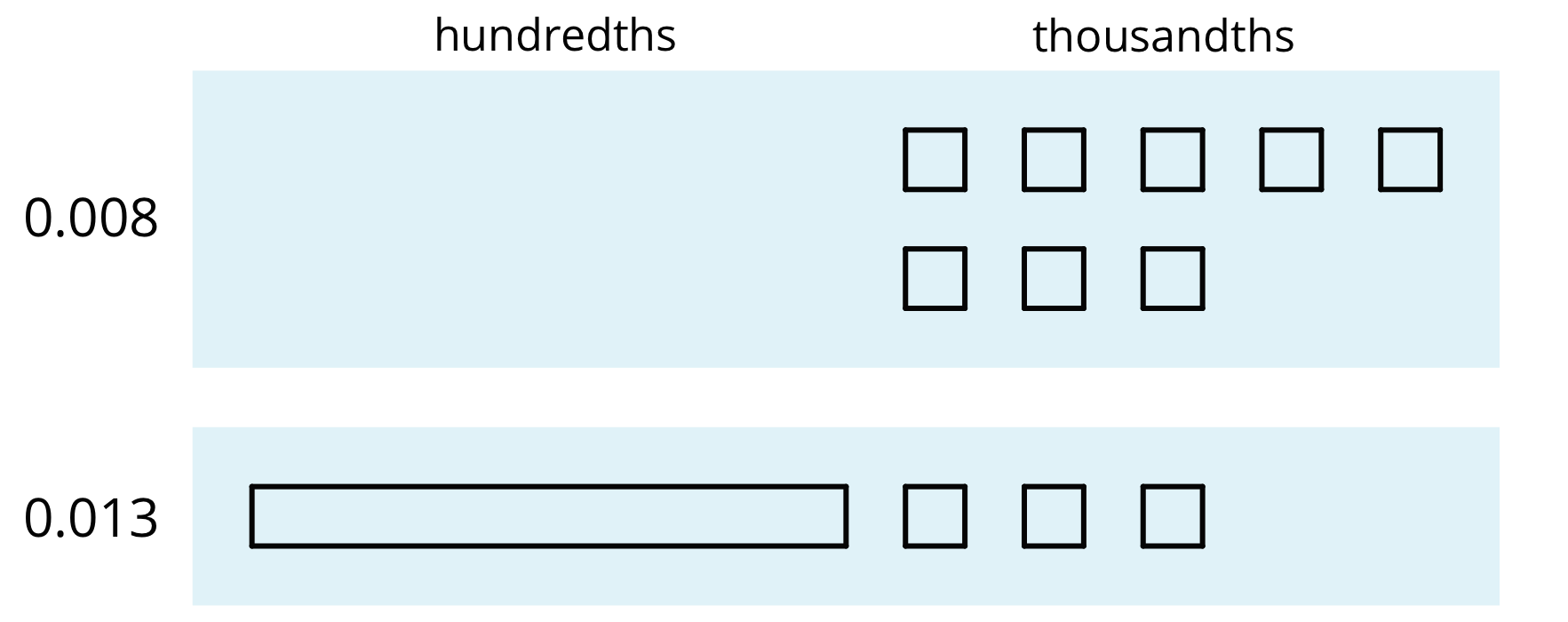
Here is a diagram of 0.008 and 0.013, where a square represents 0.001 and a rectangle (made up of ten squares) represents 0.01.
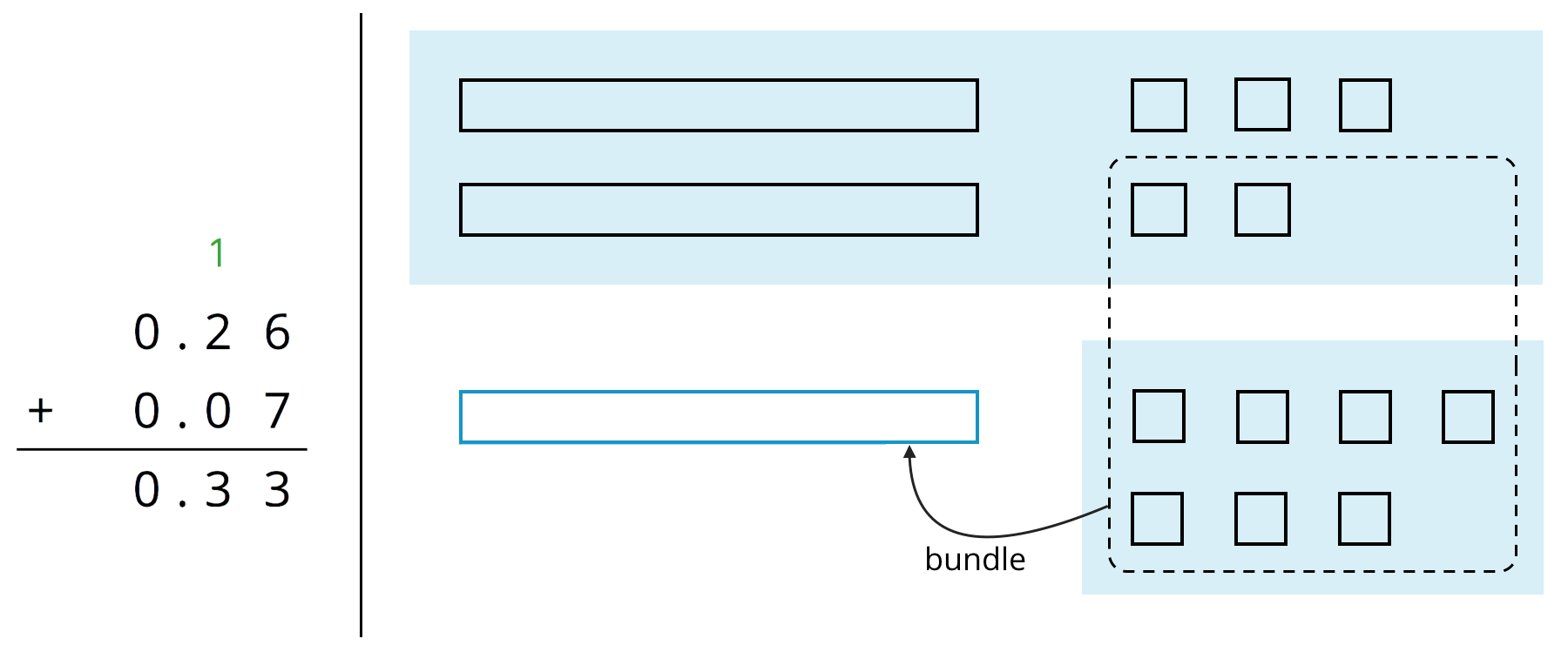
To find the sum, we can “bundle” (or compose) 10 thousandths as 1 hundredth.
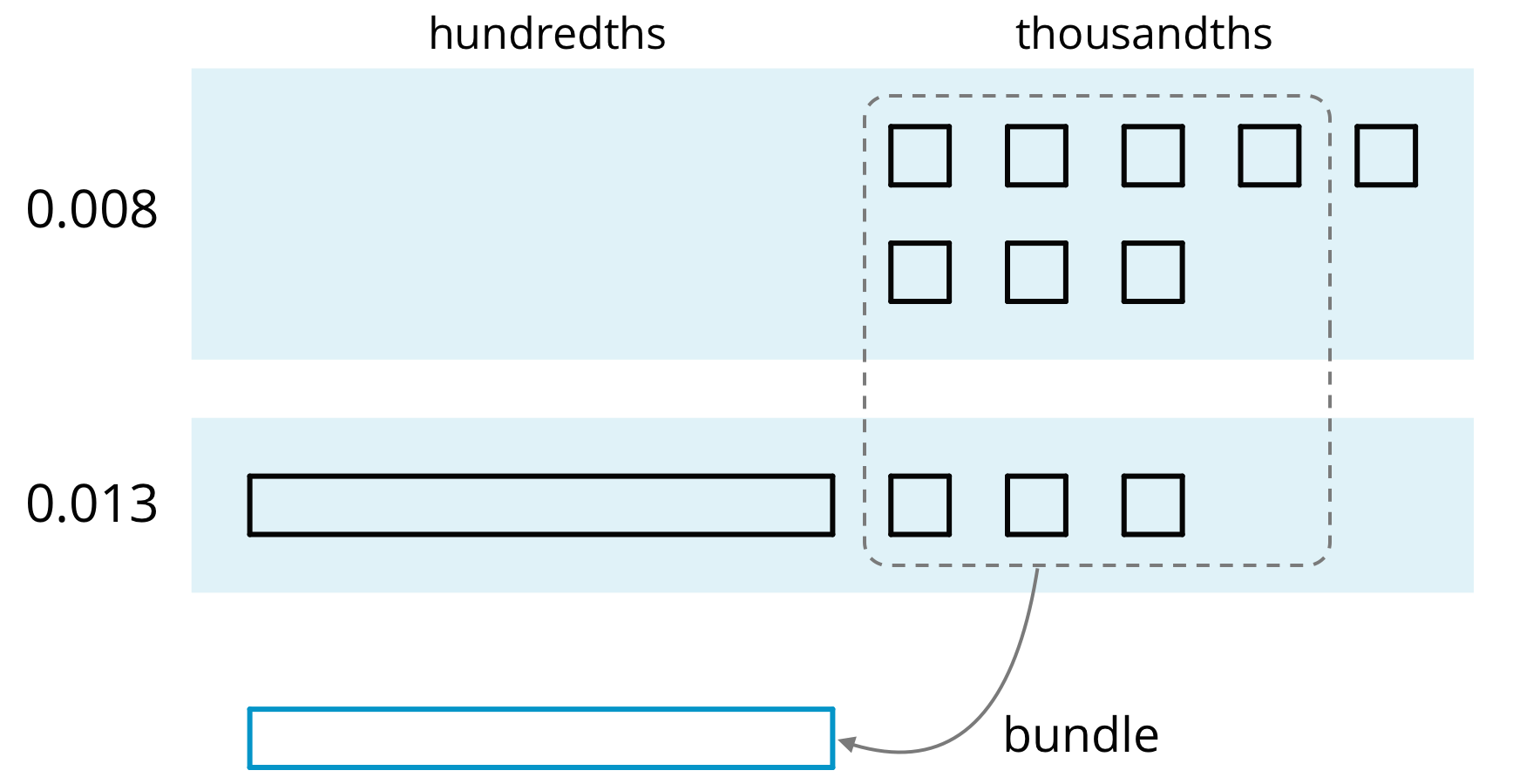
Here is a diagram of the sum, which shows 2 hundredths and 1 thousandth.
We can use vertical calculation to find $0.008 + 0.013$. Notice that here 10 thousandths are also bundled (or composed) as 1 hundredth.