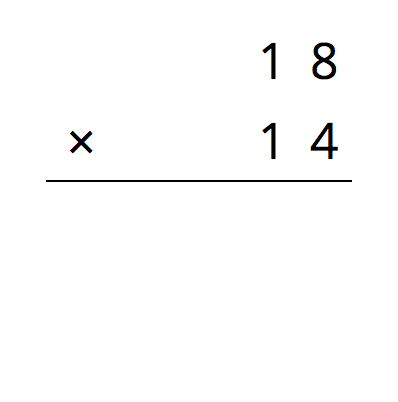Suppose that we want to calculate the product of two numbers that are written in base ten. To explain how, we can use what we know about base-ten numbers and areas of rectangles.
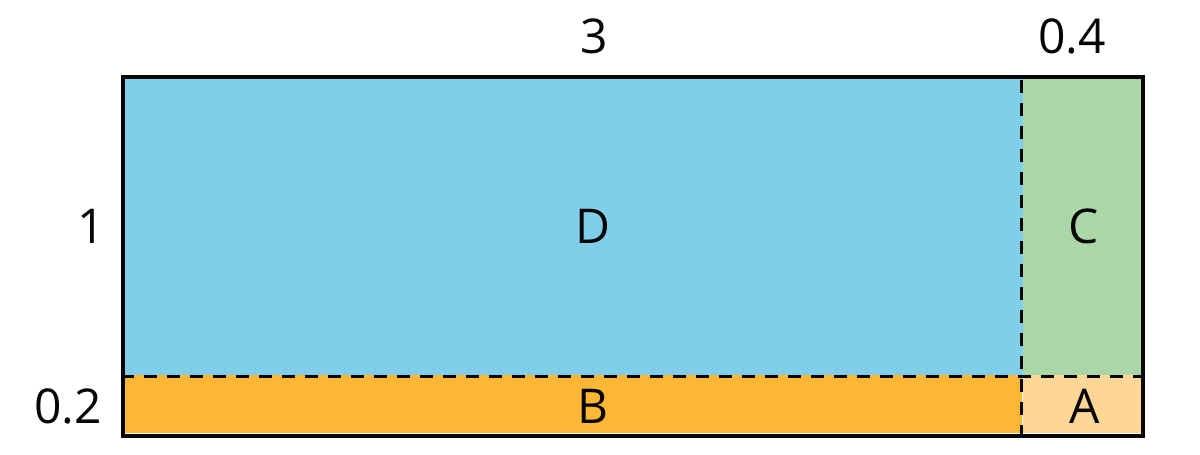
Here is a diagram of a rectangle whose side lengths are 3.4 units and 1.2 units. Its area, in square units, is the product
$(3.4) \boldcdot (1.2)$. To calculate this product and find the area of the rectangle, we can decompose each side length into its base-ten units, $3.4 = 3 + 0.4$ and $1.2= 1 + 0.2$, decomposing the rectangle into four smaller sub-rectangles.
We can rewrite the product and expand it twice:
\(\begin{align} (3.4) \boldcdot (1.2) &= (3 + 0.4) \boldcdot (1 + 0.2)\\ &=(3 + 0.4) \boldcdot 1 + (3 + 0.4) \boldcdot 0.2\\ &=3 \boldcdot 1+ 3 \boldcdot (0.2)+ (0.4) \boldcdot 1 + (0.4)\boldcdot (0.2)\\ \end{align}\)
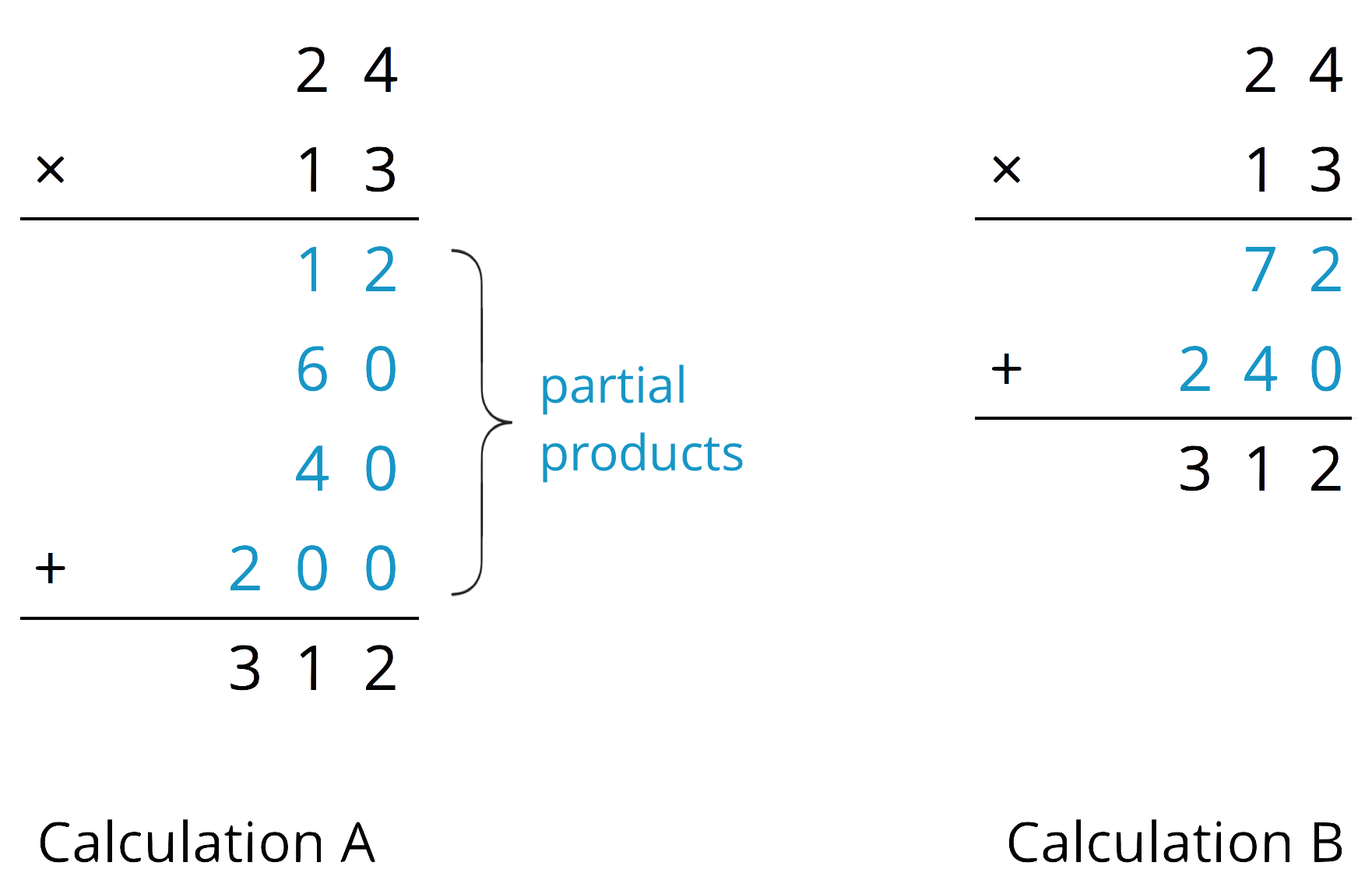
In the last expression, each of the four terms is called a partial product. Each partial product gives the area of a sub-rectangle in the diagram. The sum of the four partial products gives the area of the entire rectangle.
We can show the horizontal calculations above as two vertical calculations.
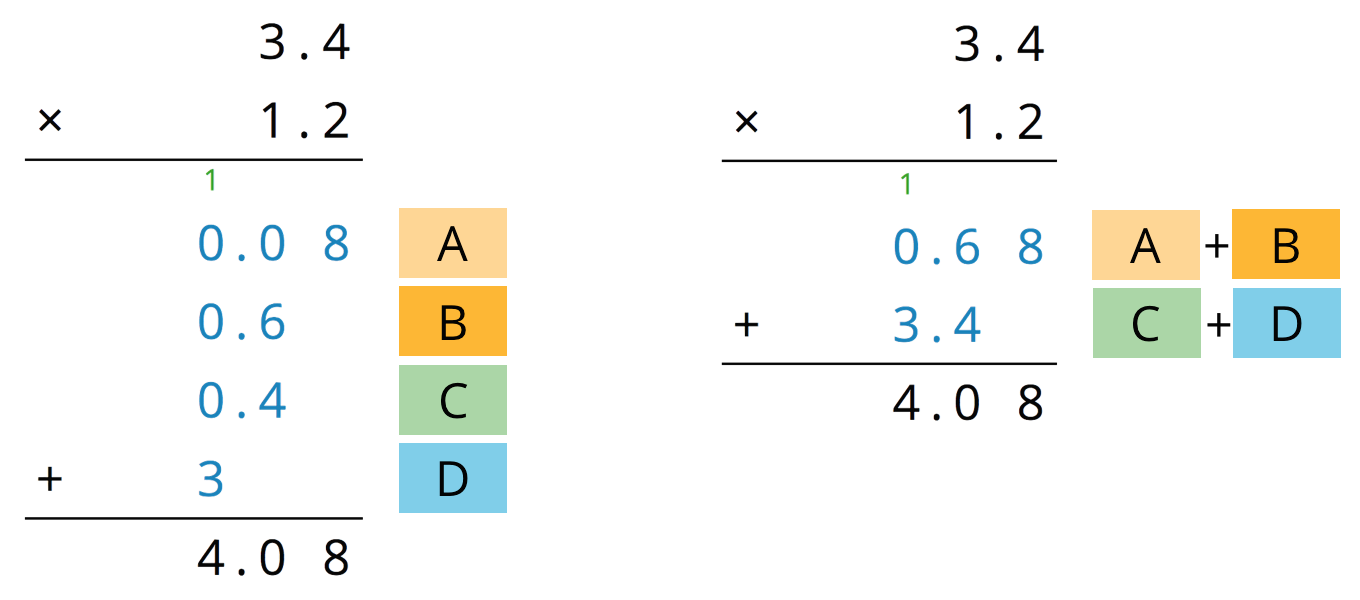
The vertical calculation on the left is an example of the partial products method. It shows the values of each partial product and the letter of the corresponding sub-rectangle. Each partial product gives an area:
- A is 0.2 unit by 0.4 unit, so its area is 0.08 square unit.
- B is 3 unit by 0.2 unit, so its area is 0.6 square unit.
- C is 0.4 unit by 1 unit, so its area is 0.4 square unit.
- D is 3 units by 1 unit, so its area is 3 square units.
- The sum of the partial products is $0.08 + 0.6 +0.4+ 3$, so the area of the rectangle is 4.08 square units.
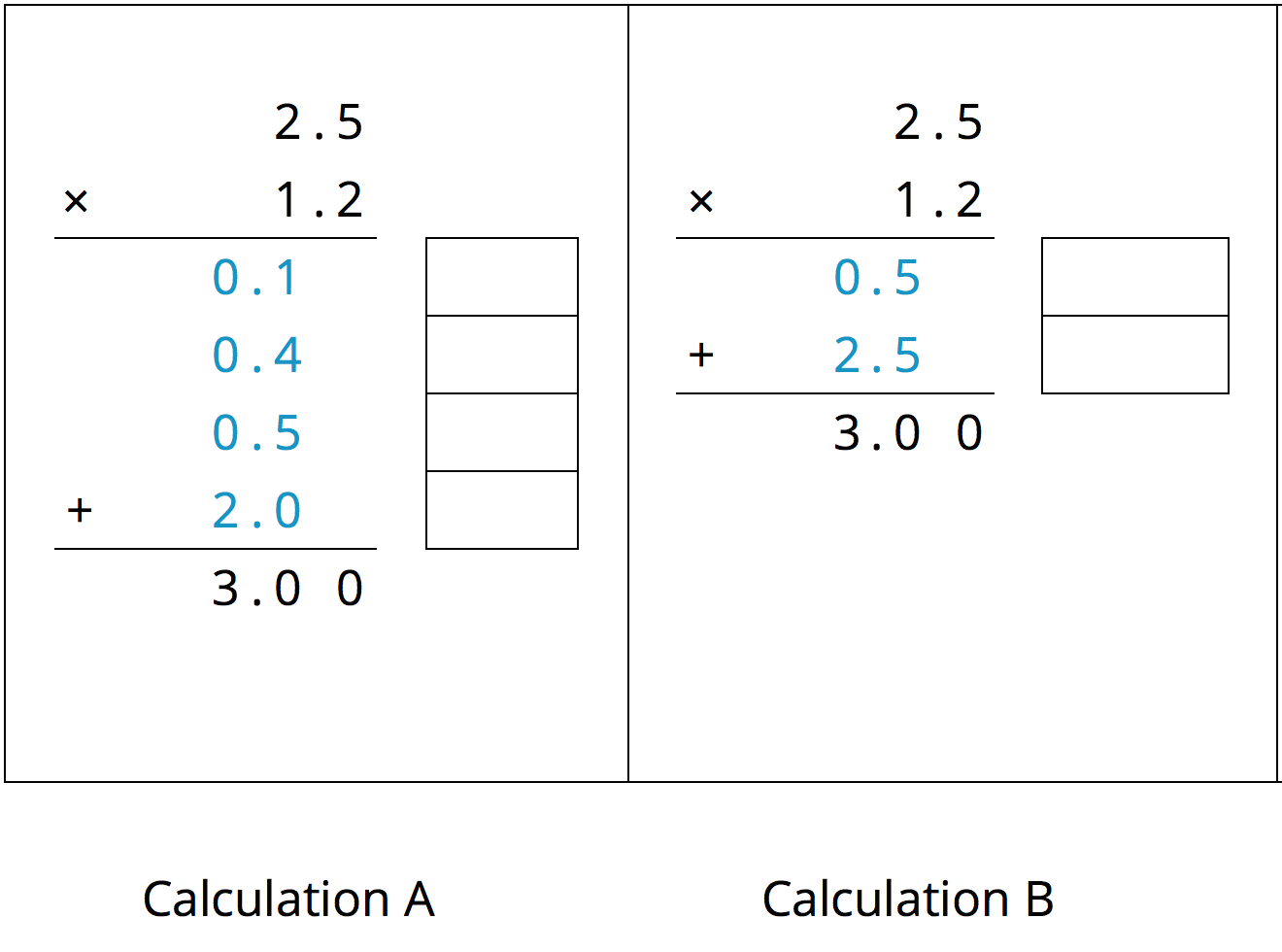
The calculation on the right shows the values of two products. Each value gives a combined area of two sub-rectangles:
- The combined regions of A and B have an area of 0.68 square units; 0.68 is the value of $(3 + 0.4) \boldcdot 0.2$.
- The combined regions of C and D have an area of 3.4 square units; 3.4 is the value of $(3 + 0.4) \boldcdot 1$.
- The sum of the values of two products is $0.68 + 3.4$, so the area of the rectangle is 4.08 square units.