8.1: Number Talk: Twenty Times a Number
Evaluate mentally.
$20 \boldcdot 5$
$20 \boldcdot (0.8)$
$20 \boldcdot (0.04)$
$20 \boldcdot (5.84)$
Let’s multiply decimals.
Evaluate mentally.
$20 \boldcdot 5$
$20 \boldcdot (0.8)$
$20 \boldcdot (0.04)$
$20 \boldcdot (5.84)$
A common way to find a product of decimals is to calculate a product of whole numbers, then place the decimal point in the product.
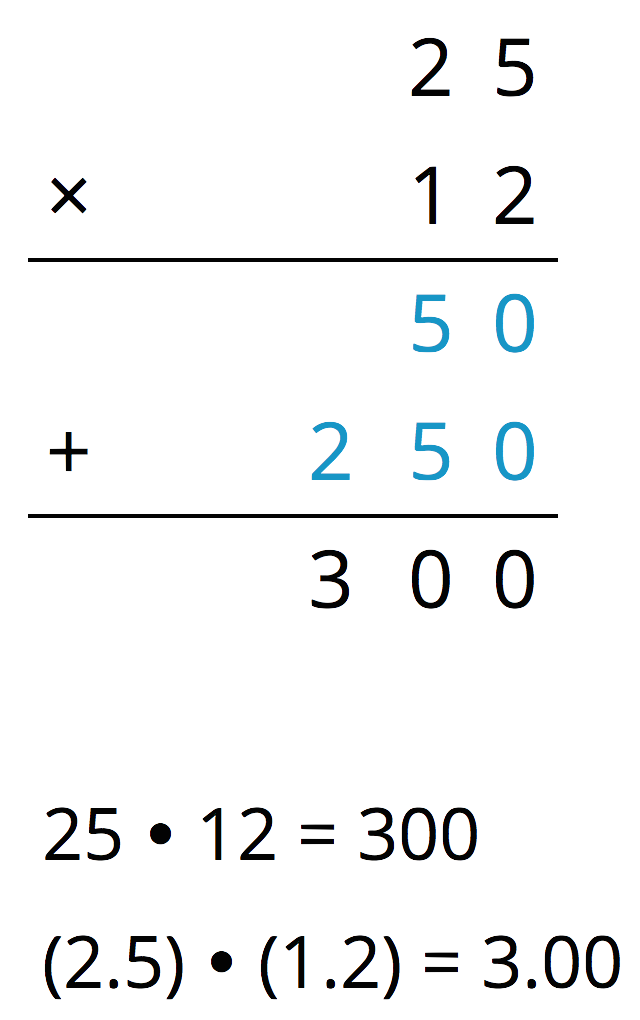
Here is an example for $(2.5) \boldcdot (1.2)$.
Use what you know about decimals and place value to explain why the decimal point of the product is placed where it is.
Use the method shown in the first question to calculate each product.
Use area diagrams to check your earlier calculations. For each problem:
$(4.6) \boldcdot (0.9)$


About how many centimeters are in 6.25 inches if 1 inch is about 2.5 centimeters? Show your reasoning.
Calculate each product. Show your reasoning. If you get stuck, draw an area diagram to help.
A rectangular playground is 18.2 meters by 12.75 meters.
Write the following expressions as decimals.
We can use $84\boldcdot 43$ and what we know about place value to find $(8.4) \boldcdot (4.3)$.
Since 8.4 is 84 tenths and 4.3 is 43 tenths, then: $$(8.4) \boldcdot (4.3) =\frac{84}{10} \boldcdot \frac{43}{10}$$$$(8.4) \boldcdot (4.3) =\frac{84 \boldcdot 43}{100}$$
That means we can compute $84\boldcdot 43$ and then divide by 100 to find $(8.4) \boldcdot (4.3)$.
$$84\boldcdot 43= 3612$$ $$(8.4) \boldcdot (4.3) = 36.12$$
Using fractions such as $\frac{1}{10}$, $\frac{1}{100}$, and $\frac{1}{1,000}$ allows us to find the product of two decimals using the following steps:
We know multiplying by fractions such as $\frac{1}{10}$, $\frac{1}{100}$, and $\frac{1}{1,000}$ is the same as dividing by 10, 100, and 1,000, respectively. This means we can move the decimal point in the whole-number product to the left the appropriate number of spaces to correctly place the decimal point.