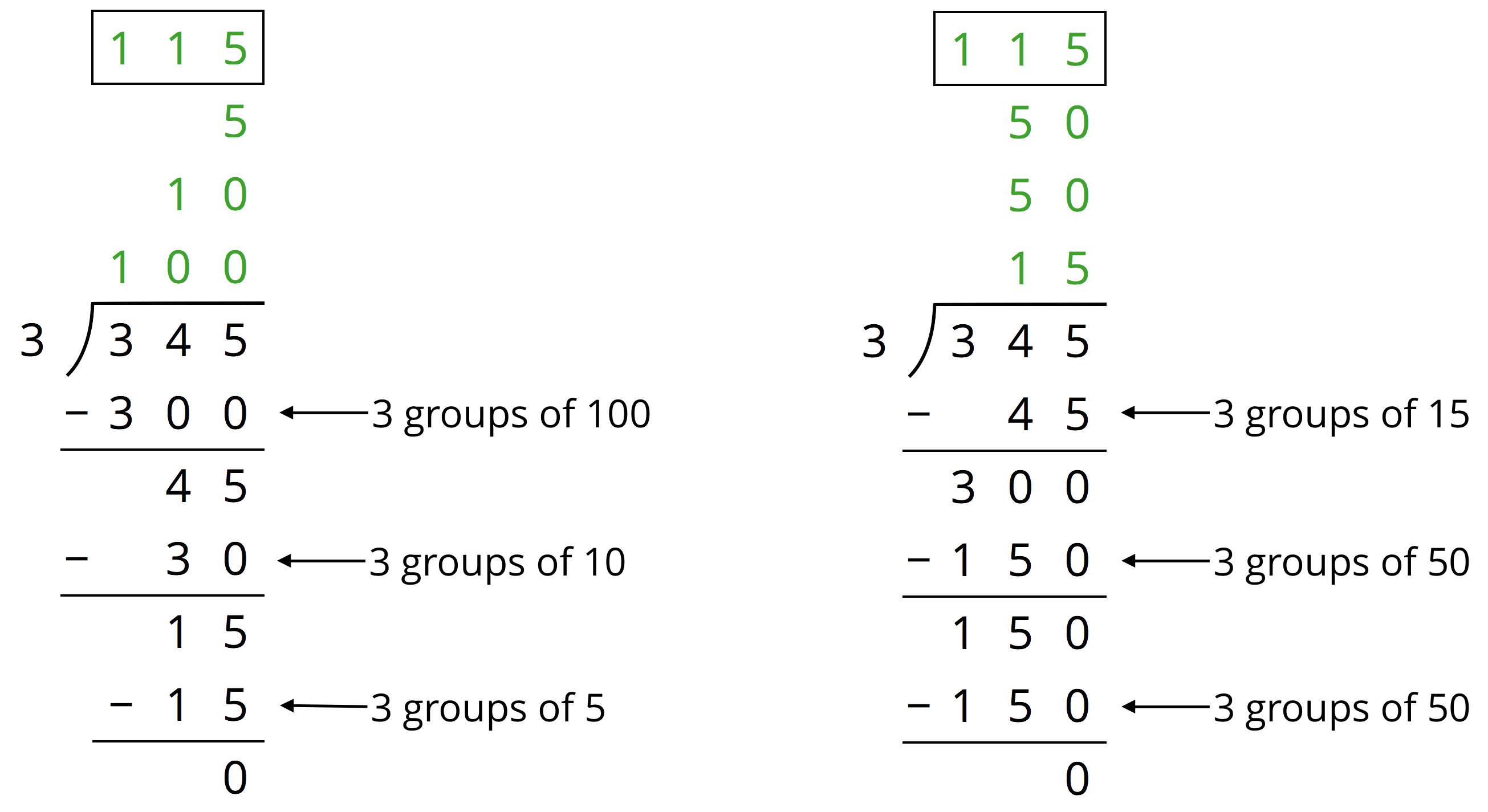We can find the quotient $345\div 3$ in different ways.
One way is to use a base-ten diagram to represent the hundreds, tens, and ones and to create equal-sized groups.

We can think of the division by 3 as splitting up 345 into 3 equal groups.
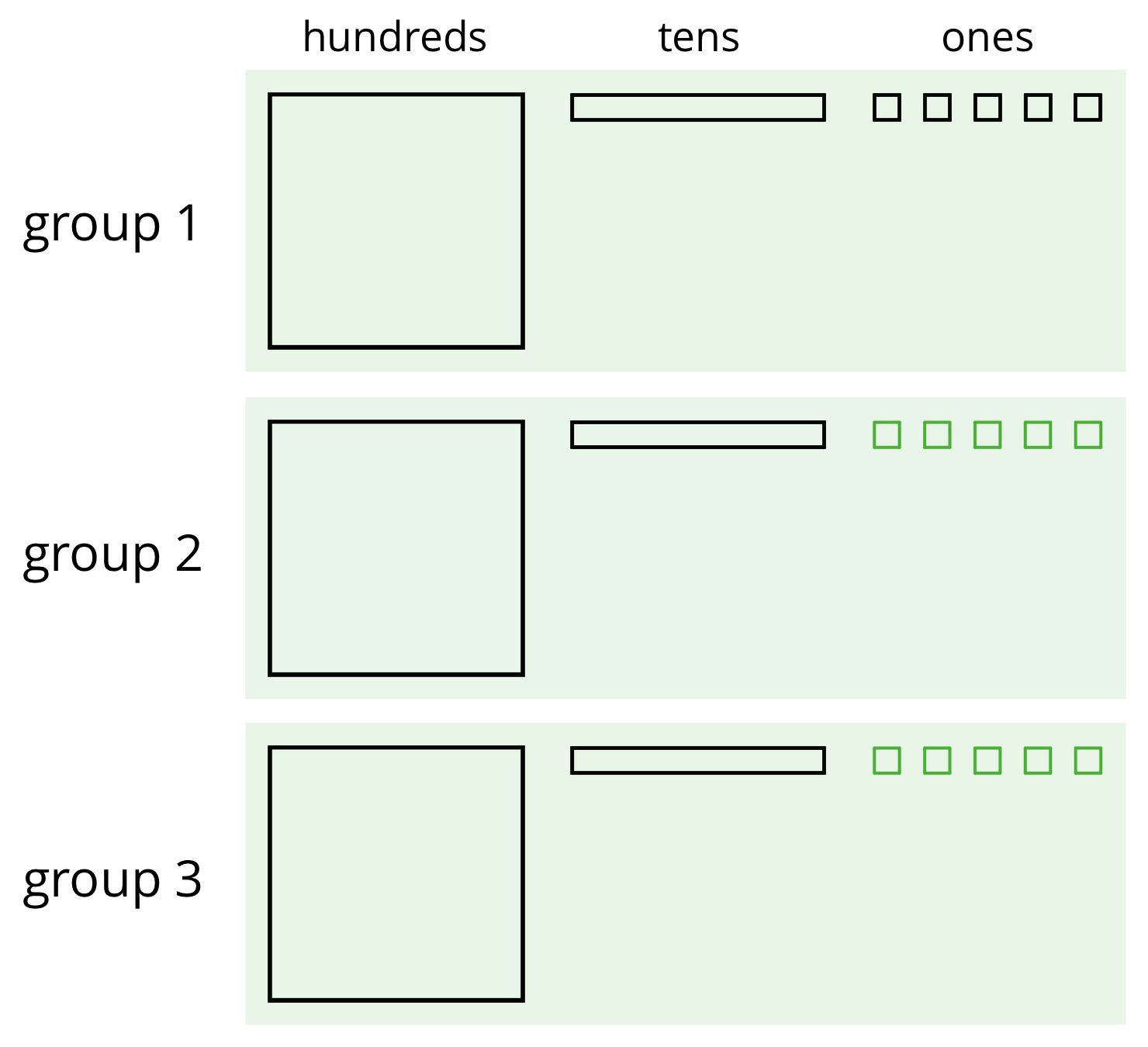
Each group has 1 hundred, 1 ten, and 5 ones, so $345 \div 3 = 115$. Notice that in order to split 345 into 3 equal groups, one of the tens had to be unbundled or decomposed into 10 ones.
Another way to divide 345 by 3 is by using the partial quotients method, in which we keep subtracting 3 groups of some amount from 345.
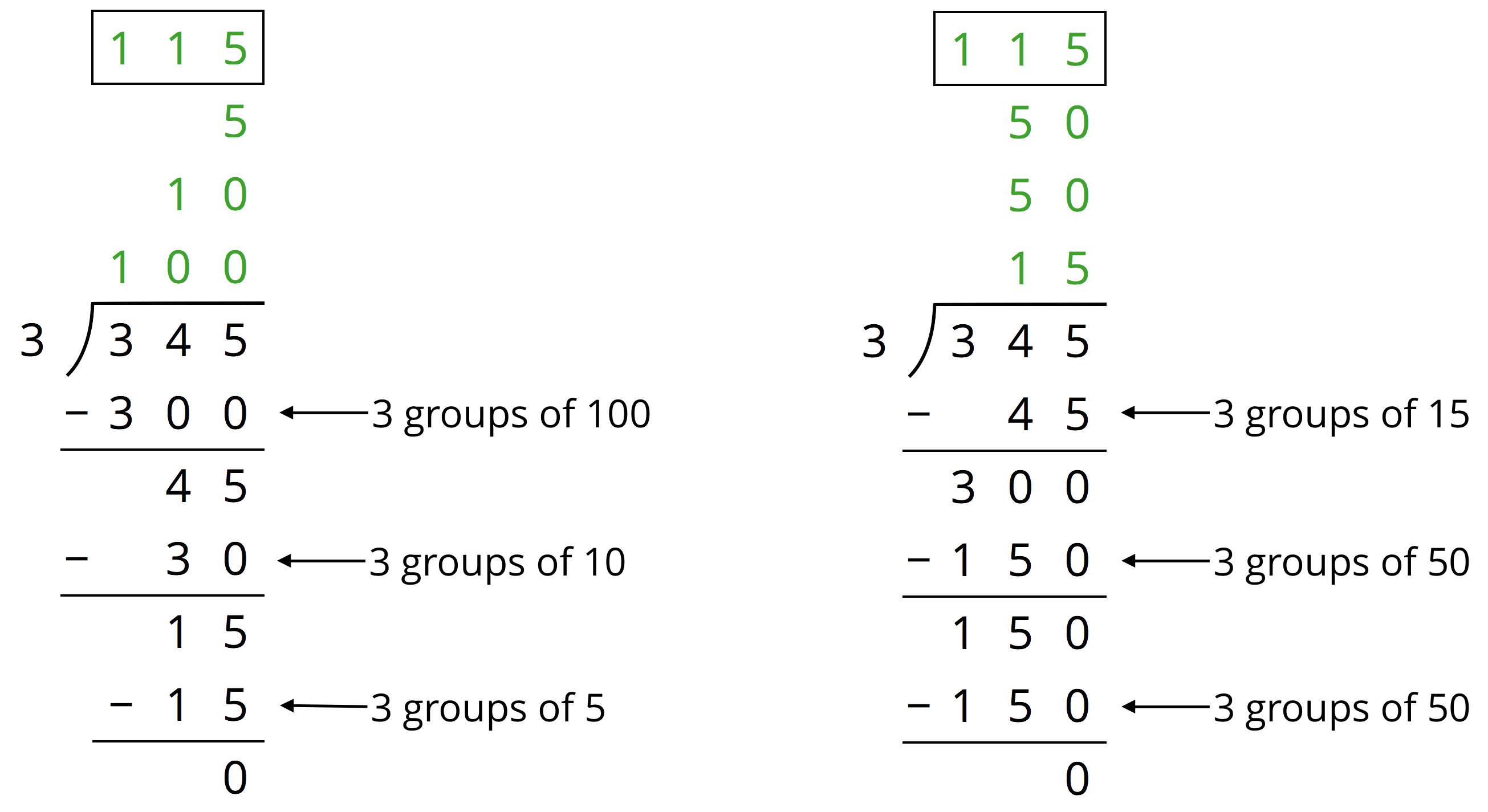
- In the calculation on the left, first we subtract 3 groups of 100, then 3 groups of 10, and then 3 groups of 5. Adding up the partial quotients ($100+10+5$) gives us 115.
- The calculation on the right shows a different amount per group subtracted each time (3 groups of 15, 3 groups of 50, and 3 more groups of 50), but the total amount in each of the 3 groups is still 115. There are other ways of calculating $345 \div 3$ using the partial quotients method.
Both the base-ten diagrams and partial quotients methods are effective. If, however, the dividend and divisor are large, as in $1,\!248 \div 26$, then the base-ten diagrams will be time-consuming.