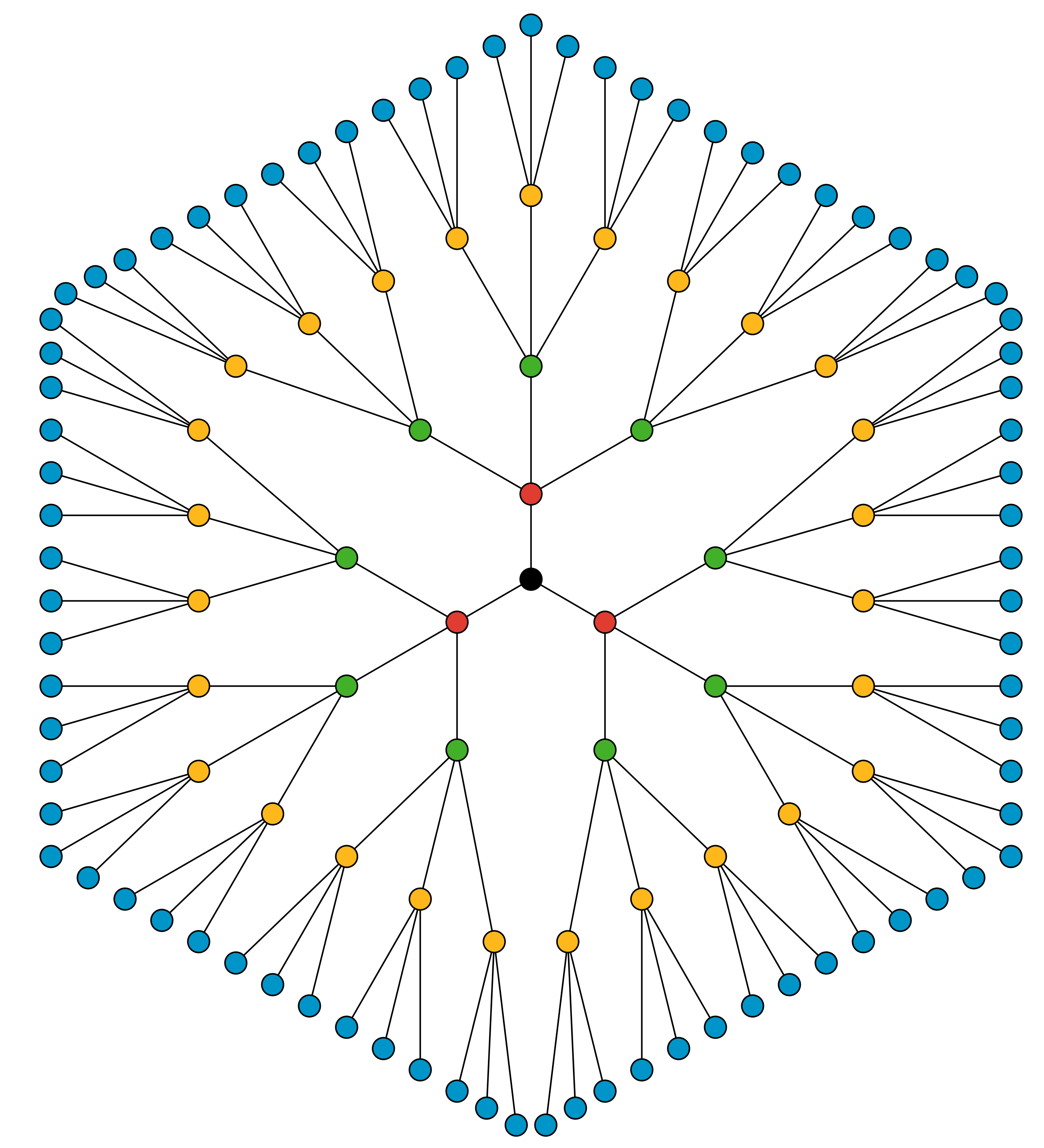
12.1: Notice and Wonder: Dots and Lines
What do you notice? What do you wonder?
Let’s see how exponents show repeated multiplication.
What do you notice? What do you wonder?

You are walking along and you find a brass bottle that looks really, really old. There appears to be some writing on the bottle! You try to clean off some dirt to read it better. A genie appears! He is so happy to be free. He wants to repay you. He offers two ways to repay you and you must choose one:
Explore the applet. (Why do you think it stops?)
A scientist is growing a colony of bacteria in a petri dish. She knows that the bacteria are growing and that the number of bacteria doubles every hour.
When she leaves the lab at 5 p.m., there are 100 bacteria in the dish. When she comes back the next morning at 9 a.m., the dish is completely full of bacteria. At what time was the dish half full?
Here are some expressions. All but one of them equals 16. Find the one that is not equal to 16 and explain how you know.
$2^3\boldcdot 2$
$4^2$
$\frac{2^5}{2}$
$8^2$
When we write an expression like $2^n$, we call $n$ the exponent.
If $n$ is a positive whole number, it tells how many factors of 2 we should multiply to find the value of the expression. For example, $2^1=2$, and $2^5=2 \boldcdot 2 \boldcdot 2 \boldcdot 2 \boldcdot 2$.
There are different ways to say $2^5$. We can say “two raised to the power of five” or “two to the fifth power” or just “two to the fifth.”