A hanger stays balanced when the weights on both sides are equal. We can change the weights and the hanger will stay balanced as long as both sides are changed in the same way. For example, adding 2 pounds to each side of a balanced hanger will keep it balanced. Removing half of the weight from each side will also keep it balanced.
An equation can be compared to a balanced hanger. We can change the equation, but for a true equation to remain true, the same thing must be done to both sides of the equal sign. If we add or subtract the same number on each side, or multiply or divide each side by the same number, the new equation will still be true.
This way of thinking can help us find solutions to equations. Instead of checking different values, we can think about subtracting the same amount from each side or dividing each side by the same number.

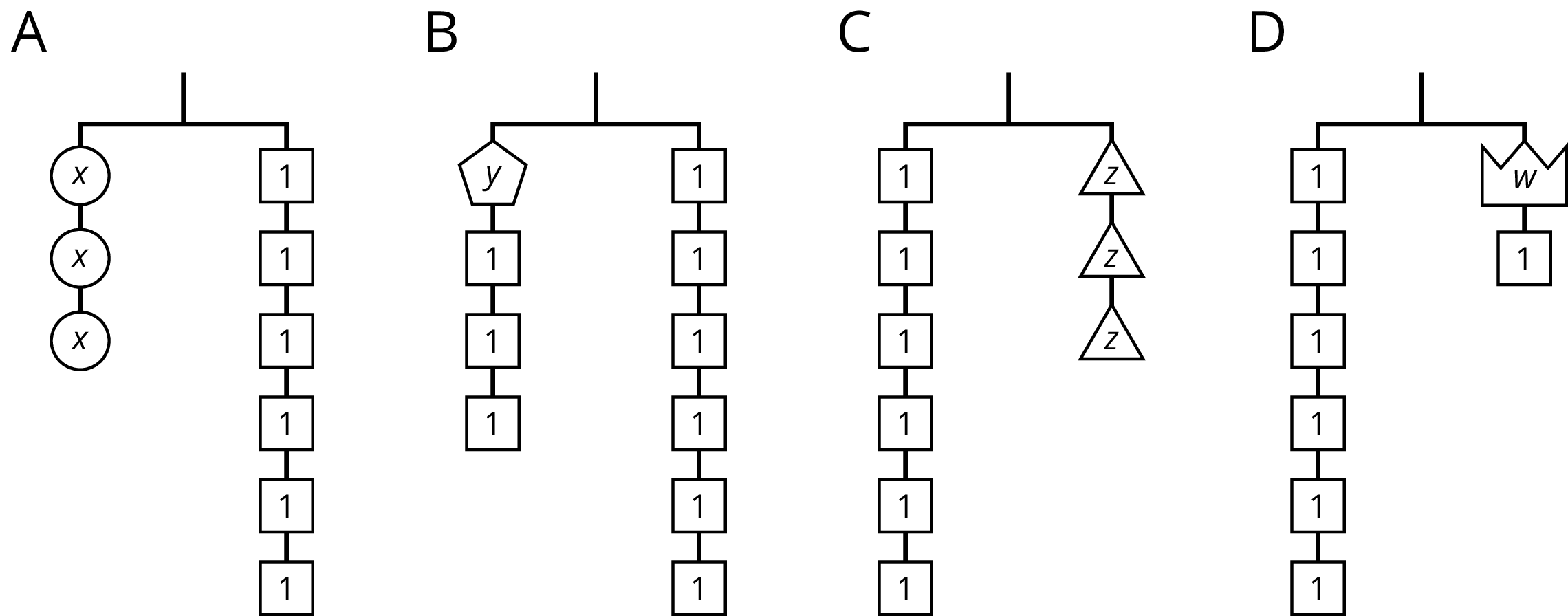
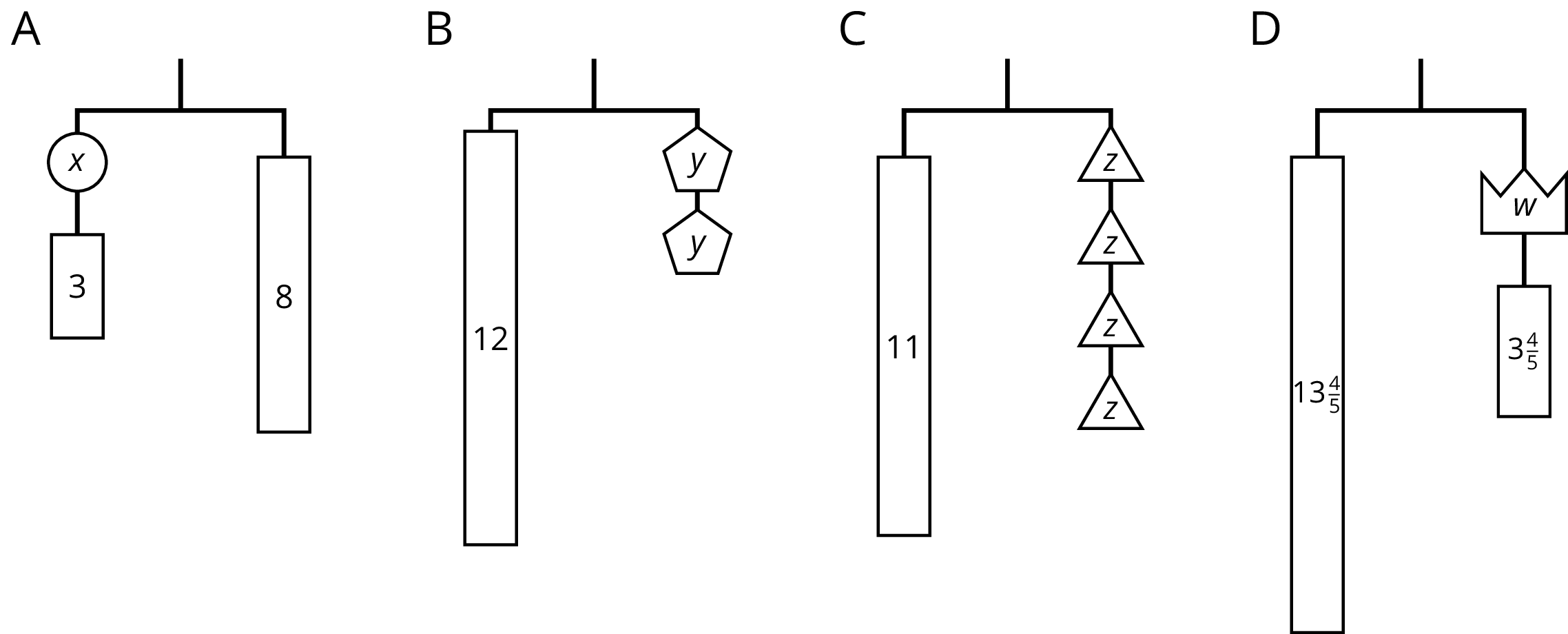
Diagram A can be represented by the equation $3x=11$.
If we break the 11 into 3 equal parts, each part will have the same weight as a block with an $x$.
Splitting each side of the hanger into 3 equal parts is the same as dividing each side of the equation by 3.
- $3x$ divided by 3 is $x$.
- 11 divided by 3 is $\frac{11}{3}$.
- If $3x=11$ is true, then $x=\frac{11}{3}$ is true.
- The solution to $3x=11$ is $\frac{11}{3}$.
Diagram B can be represented with the equation $11=y+5$.
If we remove a weight of 5 from each side of the hanger, it will stay in balance.
Removing 5 from each side of the hanger is the same as subtracting 5 from each side of the equation.
- $11-5$ is 6.
- $y+5-5$ is $y$.
- If $11=y+5$ is true, then $6=y$ is true.
- The solution to $11=y+5$ is 6.