2.1: A Point on the Number Line
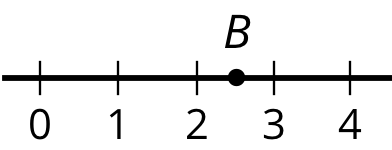
Which of the following numbers could be $B$?
2.5
$\frac25$
$\frac{5}{2}$
$\frac{25}{10}$
2.49
Let’s plot positive and negative numbers on the number line.

Which of the following numbers could be $B$?
2.5
$\frac25$
$\frac{5}{2}$
$\frac{25}{10}$
2.49
Here are five thermometers. The first four thermometers show temperatures in Celsius. Write the temperatures in the blanks.
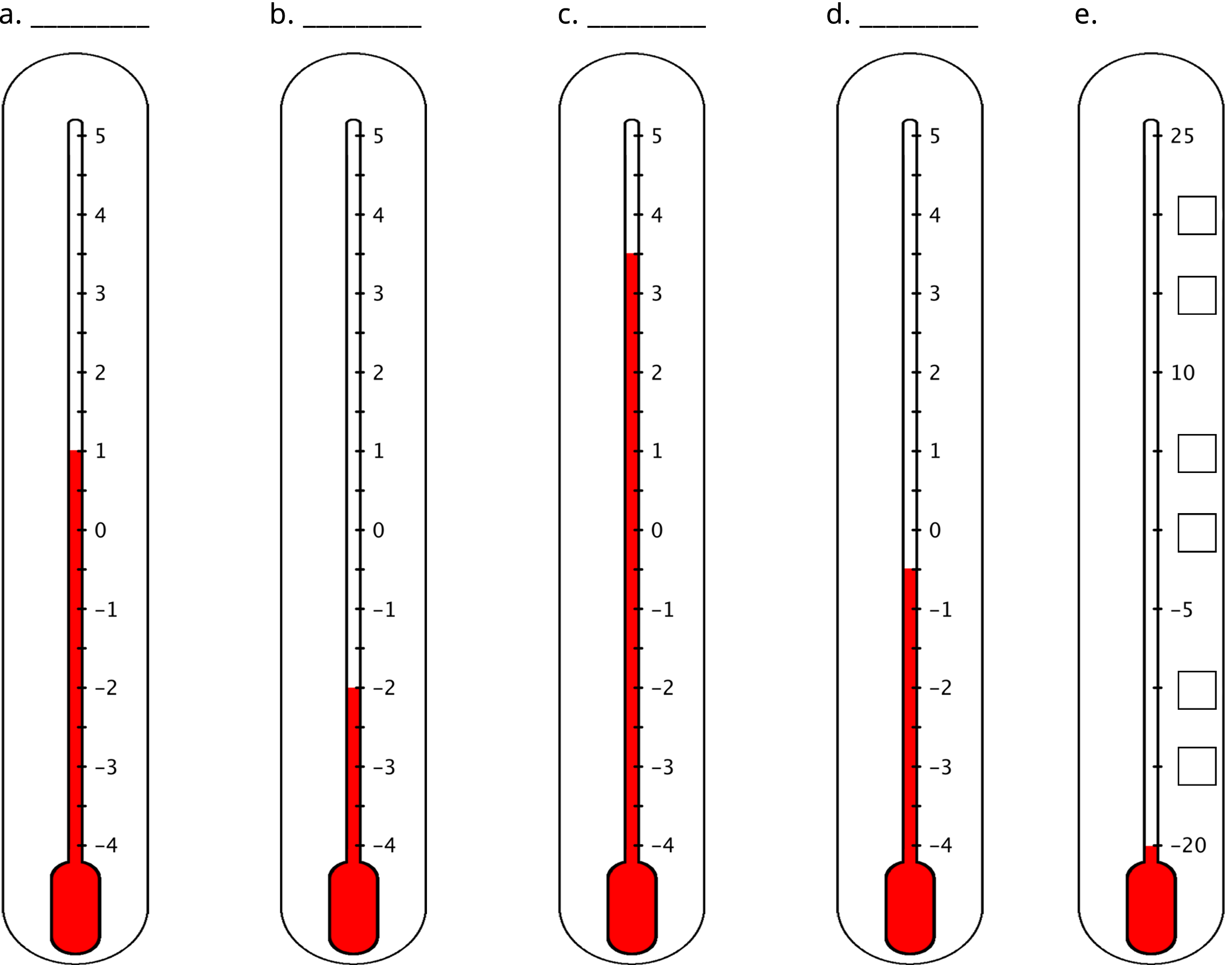
The last thermometer is missing some numbers. Write them in the boxes.

Your teacher will give you a sheet of tracing paper on which to draw a number line.
Follow the steps to make your own number line.
Use your number line to answer these questions:
Pause here so your teacher can review your work.
Here is a number line with some points labeled with letters. Determine the location of points $P$, $X$, and $Y$.
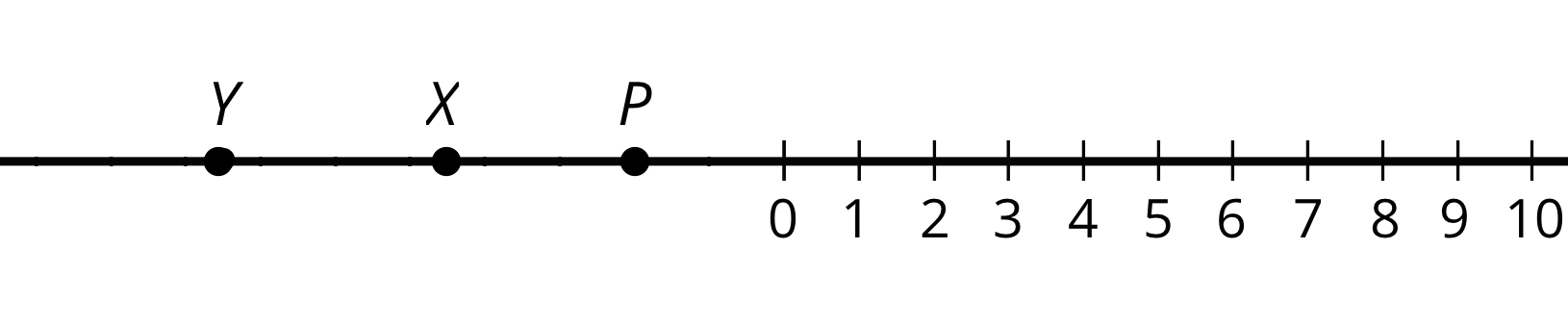
If you get stuck, trace the number line and points onto a sheet of tracing paper, fold it so that a vertical crease goes through 0, and use the folded number line to help you find the unknown values.
At noon, the temperatures in Portland, Maine and Phoenix, Arizona had opposite values. The temperature in Portland was $18^\circ \text{C}$ lower than in Phoenix. What was the temperature in each city? Explain your reasoning.
Here is a number line labeled with positive and negative numbers. The number 4 is positive, so its location is 4 units to the right of 0 on the number line. The number -1.1 is negative, so its location is 1.1 units to the left of 0 on the number line.

We say that the opposite of 8.3 is -8.3, and that the opposite of $\frac {\text{-}3}{2}$ is $\frac32$. Any pair of numbers that are equally far from 0 are called opposites.
Points $A$ and $B$ are opposites because they are both 2.5 units away from 0, even though $A$ is to the left of 0 and $B$ is to the right of 0.
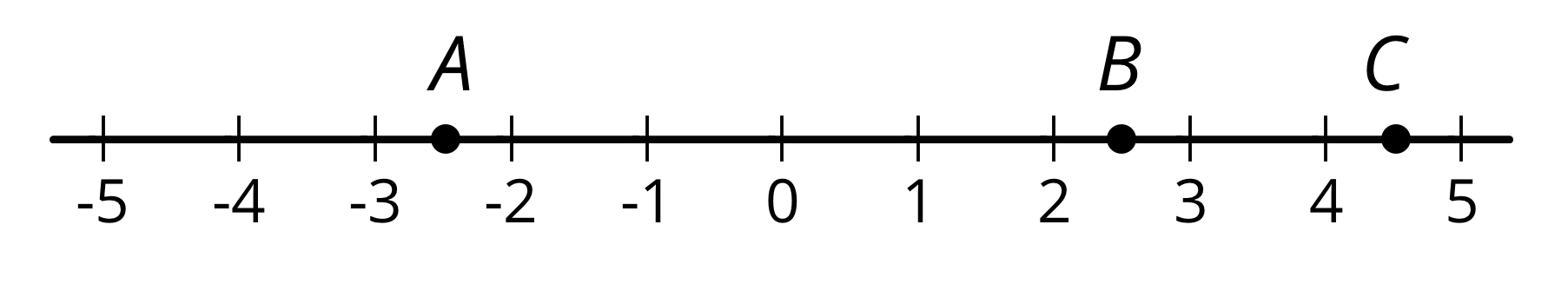
A positive number has a negative number for its opposite. A negative number has a positive number for its opposite. The opposite of 0 is itself.
You have worked with positive numbers for many years. All of the positive numbers you have seen—whole and non-whole numbers—can be thought of as fractions and can be located on a the number line.
To locate a non-whole number on a number line, we can divide the distance between two whole numbers into fractional parts and then count the number of parts. For example, 2.7 can be written as $2 \frac {7}{10}$. The segment between 2 and 3 can be partitioned into 10 equal parts or 10 tenths. From 2, we can count 7 of the tenths to locate 2.7 on the number line.
All of the fractions and their opposites are what we call rational numbers. For example, 4, -1.1, 8.3, -8.3, $\frac {\text{-}3}{2}$, and $\frac32$ are all rational numbers.
Two numbers are opposites of each other if they are the same distance from 0 on the number line, but on opposite sides.
A rational number is a fraction or the opposite of a fraction. Remember that a fraction is a point on the number line that you get by dividing the unit interval into $b$ equal parts and finding the point that is $a$ of them from 0. We can always write a fraction in the form $\frac{a}{b}$ where $a$ and $b$ are whole numbers, with $b$ not equal to 0, but there are other ways to write them. For example, 0.7 is a fraction because it is the point on the number line you get by dividing the unit interval into 10 equal parts and finding the point that is 7 of those parts away from 0. We can also write this number as $\frac{7}{10}$.