6.1: Number Talk: Closer to Zero
For each pair of expressions, decide mentally which one has a value that is closer to 0.
$\frac{9}{11}$ or $\frac{15}{11}$
$\frac15$ or $\frac19$
$1.25$ or $\frac54$
$0.01$ or $0.001$
Let’s explore distances from zero more closely.
For each pair of expressions, decide mentally which one has a value that is closer to 0.
$\frac{9}{11}$ or $\frac{15}{11}$
$\frac15$ or $\frac19$
$1.25$ or $\frac54$
$0.01$ or $0.001$
Move the bug to a starting point, choose a jump distance, and press the jump button. You may need to zoom in or out if your bug jumps off the screen.
A part of the city of New Orleans is 6 feet below sea level. We can use “-6 feet” to describe its elevation, and “$|\text-6|$ feet” to describe its vertical distance from sea level. In the context of elevation, what would each of the following numbers describe?
We write “$\text-5^\circ \text{C}$” to describe a temperature that is 5 degrees Celsius below freezing point and “$5^\circ \text{C}$” for a temperature that is 5 degrees above freezing. In this context, what do each of the following numbers describe?
Which temperature is colder: $\text-6^\circ \text{C}$ or $3^\circ \text{C}$?
Which temperature is closer to freezing temperature: $\text-6^\circ \text{C}$ or $3^\circ \text{C}$?
We compare numbers by comparing their positions on the number line: the one farther to the right is greater; the one farther to the left is less.
Sometimes we wish to compare which one is closer to or farther from 0. For example, we may want to know how far away the temperature is from the freezing point of $0 ^\circ \text{C}$, regardless of whether it is above or below freezing.
The absolute value of a number tells us its distance from 0.
The absolute value of -4 is 4, because -4 is 4 units to the left of 0. The absolute value of 4 is also 4, because 4 is 4 units to the right of 0. Opposites always have the same absolute value because they both have the same distance from 0.
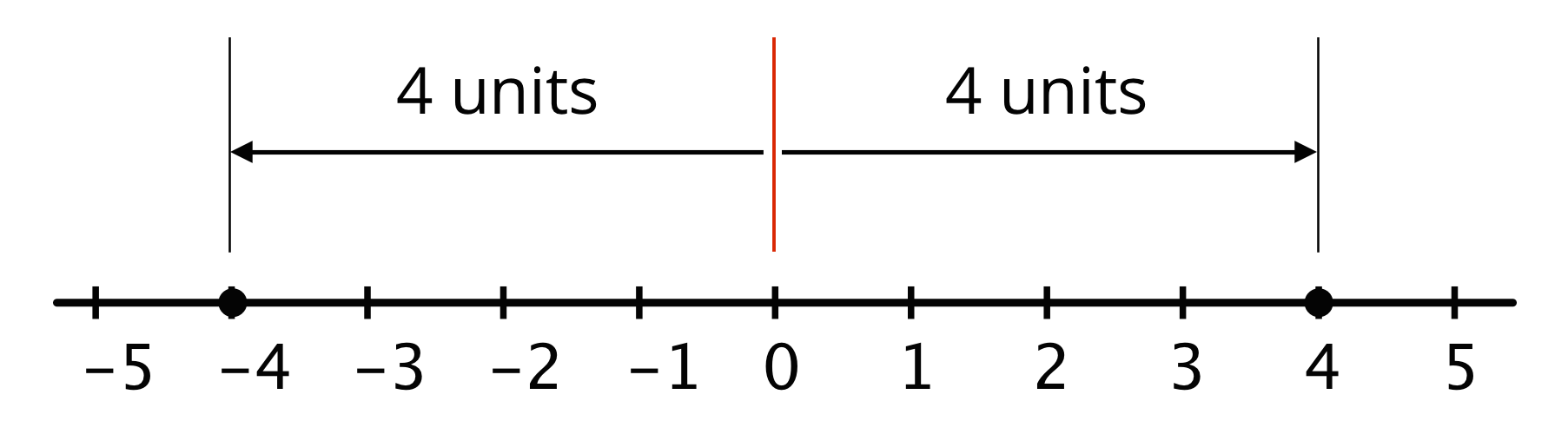
The distance from 0 to itself is 0, so the absolute value of 0 is 0. Zero is the only number whose distance to 0 is 0. For all other absolute values, there are always two numbers—one positive and one negative—that have that distance from 0.
To say “the absolute value of 4,” we write: $$|4|$$
To say that “the absolute value of -8 is 8,” we write: $$|\text- 8| = 8$$
The absolute value of a number is its distance from 0 on the number line.