- -5
- 28
- -10.4
Unit 7: Practice Problem Sets
Lesson 1
Problem 1
- Is a temperature of -11 degrees warmer or colder than a temperature of -15 degrees?
- Is an elevation of -10 feet closer or farther from the surface of the ocean than an elevation of -8 feet?
- It was 8 degrees at nightfall. The temperature dropped 10 degrees by midnight. What was the temperature at midnight?
- A diver is 25 feet below sea level. After he swims up 15 feet toward the surface, what is his elevation?
Problem 2
-
A whale is at the surface of the ocean to breathe. What is the whale’s elevation?
-
The whale swims down 300 feet to feed. What is the whale’s elevation now?
-
The whale swims down 150 more feet more. What is the whale’s elevation now?
-
Plot each of the three elevations as a point on a vertical number line. Label each point with its numeric value.
Problem 3 (from Unit 6, Lesson 5)
Problem 4 (from Unit 6, Lesson 4)
Write an equation to represent each situation and then solve the equation.
- Andre drinks 15 ounces of water, which is $\frac35$ of a bottle. How much does the bottle hold? Use $x$ for the number of ounces of water the bottle holds.
- A bottle holds 15 ounces of water. Jada drank 8.5 ounces of water. How many ounces of water are left in the bottle? Use $y$ for the number of ounces of water left in the bottle.
- A bottle holds $z$ ounces of water. A second bottle holds 16 ounces, which is $\frac{8}{5}$ times as much water. How much does the first bottle hold?
Problem 5 (from Unit 4, Lesson 13)
A rectangle has an area of 24 square units and a side length of $2\frac34$ units. Find the other side length of the rectangle. Show your reasoning.
Lesson 2
Problem 1
For each number, name its opposite.
- 0.875
- 0
- -8,003
Problem 2
Plot the numbers -1.5, $\frac{3}{2}$, $\text-\frac{3}{2}$, and $\text-\frac{4}{3}$ on the number line. Label each point with its numeric value.

Problem 3
Plot the following points on a number line.
- -1.5
- the opposite of -2
- the opposite of 0.5
- -2
Problem 4 (from Unit 7, Lesson 1)
- Represent each of these temperatures in degrees Fahrenheit with a positive or negative number.
- 5 degrees above zero
- 3 degrees below zero
- 6 degrees above zero
- $2\frac34$ degrees below zero
- Order the temperatures above from the coldest to the warmest.
Problem 5 (from Unit 6, Lesson 5)
Solve each equation.
- $8x = \frac{2}{3}$
- $1\frac{1}{2}=2x$
- $5x = \frac{2}{7}$
- $\frac{1}{4}x = 5$
- $\frac{1}{5}=\frac{2}{3}x$
Problem 6 (from Unit 6, Lesson 5)
Write the solution to each equation as a fraction and as a decimal.
- $2x = 3$
- $5y = 3$
- $0.3z = 0.009$
Problem 7 (from Unit 3, Lesson 4)
There are 15.24 centimeters in 6 inches.
-
How many centimeters are in 1 foot?
-
How many centimeters are in 1 yard?
Lesson 3
Problem 1
Decide whether each inequality statement is true or false. Explain your reasoning.
- $\text-5 > 2$
- $3 > \text-8$
- $\text-12 > \text-15$
- $\text-12.5 > \text-12$
Problem 2
Here is a true statement: $\text-8.7 < \text-8.4$. Select all of the statements that are equivalent to $\text-8.7 < \text-8.4$.
-
-8.7 is further to the right on the number line than -8.4.
-
-8.7 is further to the left on the number line than -8.4.
-
-8.7 is less than -8.4.
-
-8.7 is greater than -8.4.
-
-8.4 is less than -8.7.
-
-8.4 is greater than -8.7.
Problem 3 (from Unit 7, Lesson 4)
The table shows five states and the lowest point in each state.
| state | lowest elevation (feet) | |
|---|---|---|
| row 1 | California | -282 |
| row 2 | Colorado | 3350 |
| row 3 | Louisiana | -8 |
| row 4 | New Mexico | 2842 |
| row 5 | Wyoming | 3099 |
Problem 4 (from Unit 7, Lesson 2)
Plot each of the following numbers on the number line. Label each point with its numeric value.
0.4, -1.5, $\text-1\frac{7}{10}$, $\text{-}\frac{11}{10}$

Problem 5 (from Unit 6, Lesson 6)
Each lap around the track is 400 meters.
- How many meters does someone run if they run:
2 laps?
5 laps?
$x$ laps?
- If Noah ran 14 laps, how many meters did he run?
- If Noah ran 7,600 meters, how many laps did he run?
Problem 6 (from Unit 3, Lesson 16)
A stadium can seat 16,000 people at full capacity.
- If there are 13,920 people in the stadium, what percentage of the capacity is filled? Explain or show your reasoning.
- What percentage of the capacity is not filled?
Lesson 4
Problem 1
Select all of the numbers that are greater than $\text-5$.
-
1.3
-
$\text-6$
-
$\text-12$
-
$\frac{1}{7}$
-
$\text-1$
-
$\text-4$
Problem 2
Order these numbers from least to greatest: $\frac12$, 0, 1, $\text{-}1\frac{1}{2}$, $\text{-}\frac{1}{2}$, $\text-1$
Problem 3
Here are the boiling points of certain elements in degrees Celsius:
- Argon: -185.8
- Chlorine: -34
- Fluorine: -188.1
- Hydrogen: -252.87
- Krypton: -153.2
List the elements from least to greatest boiling points.
Problem 4 (from Unit 7, Lesson 2)
Problem 5 (from Unit 6, Lesson 9)
Explain how to make these calculations mentally.
- $99 + 54$
- $244 - 99$
- $99 \boldcdot 6$
- $99 \boldcdot 15$
Problem 6 (from Unit 4, Lesson 11)
Find the quotients.
- $\frac{1}{2} \div 2$
- $2 \div 2$
- $\frac{1}{2} \div \frac{1}{2}$
- $\frac{38}{79} \div\frac{38}{79}$
Problem 7 (from Unit 3, Lesson 4)
Over several months, the weight of a baby measured in pounds doubles. Does its weight measured in kilograms also double? Explain.
Lesson 5
Problem 1
Write a positive or negative number to represent each change in the high temperature.
- Tuesday’s high temperature was 4 degrees less than Monday’s high temperature.
- Wednesday’s high temperature was 3.5 degrees less than Tuesday’s high temperature.
- Thursday’s high temperature was 6.5 degrees more than Wednesday’s high temperature.
- Friday’s high temperature was 2 degrees less than Thursday’s high temperature.
Problem 2
Decide which of the following quantities can be represented by a positive number and which can be represented by a negative number. Give an example of a quantity with the opposite sign in the same situation.
- Tyler’s puppy gained 5 pounds.
- The aquarium leaked 2 gallons of water.
- Andre received a gift of \$10.
- Kiran gave a gift of \$10.
- A climber descended 550 feet.
Problem 3
Make up a situation where a quantity is changing.
- Explain what it means to have a negative change.
- Explain what it means to have a positive change.
- Give an example of each.
Problem 4 (from Unit 7, Lesson 2)
-
On the number line, label the points that are 4 units away from 0.
-
If you fold the number line so that a vertical crease goes through 0, the points you label would match up. Explain why this happens.
-
On the number line, label the points that are $\frac52$ units from 0. What is the distance between these points?

Problem 5 (from Unit 6, Lesson 12)
Evaluate each expression.
- $2^3 \boldcdot 3$
- $\frac{4^2}{2}$
- $3^1$
- $6^2 \div 4$
- ${2^3}-{2}$
- ${10^2}+{5^2}$
Lesson 6
Problem 1
On the number line, plot and label all numbers with an absolute value of $\frac32$.

Problem 2
The temperature at dawn is $6^\circ \text{C}$ away from 0. Select all the temperatures that are possible.
-
$\text-12^\circ \text{C}$
-
$\text-6^\circ \text{C}$
-
$0^\circ \text{C}$
-
$6^\circ \text{C}$
-
$12^\circ \text{C}$
Problem 3
Put these numbers in order, from least to greatest.
$|\text-2.7|$
0
1.3
$|\text-1|$
2
Problem 4 (from Unit 6, Lesson 16)
Elena donates some money to charity whenever she earns money as a babysitter. The table shows how much money, $d$, she donates for different amounts of money, $m$, that she earns.
| $d$ | 4.44 | 1.80 | 3.12 | 3.60 | 2.16 |
|---|---|---|---|---|---|
| $m$ | 37 | 15 | 26 | 30 | 18 |
- What percent of her income does Elena donate to charity? Explain or show your work.
- Which quantity, $m$ or $d$, would be the better choice for the dependent variable in an equation describing the relationship between $m$ and $d$? Explain your reasoning.
- Use your choice from the second question to write an equation that relates $m$ and $d$.
Problem 5 (from Unit 6, Lesson 12)
How many times larger is the first number in the pair than the second?
- $3^4$ is _____ times larger than $3^3$.
- $5^3$ is _____ times larger than $5^2$.
- $7^{10}$ is _____ times larger than $7^8$.
- $17^6$ is _____ times larger than $17^4$.
- $5^{10}$ is _____ times larger than $5^4$.
Problem 6 (from Unit 5, Lesson 11)
Lin’s family needs to travel 325 miles to reach her grandmother’s house.
- At 26 miles, what percentage of the trip’s distance have they completed?
- How far have they traveled when they have completed 72% of the trip’s distance?
- At 377 miles, what percentage of the trip’s distance have they completed?
Lesson 7
Problem 1
In the context of elevation, what would $|\text-7|$ feet mean?
Problem 2
Match the the statements written in English with the mathematical statements.
- The number -4 is a distance of 4 units away from 0 on the number line.
- The number -63 is more than 4 units away from 0 on the number line.
- The number 4 is greater than the number -4.
- The numbers 4 and -4 are the same distance away from 0 on the number line.
- The number -63 is less than the number 4.
- The number -63 is further away from 0 than the number 4 on the number line.
- $|\text-63| > 4$
- $\text-63 < 4$
- $|\text-63| > |4|$
- $|\text-4| = 4$
- $4 > \text-4$
- $|4| = |\text-4|$
Problem 3
Compare each pair of expressions using >, <, or =.
-
$\text-32$ _____ $15$
-
$|\text-32|$ _____ $|15|$
-
$5$ _____ $\text-5$
-
$|5|$ _____ $|\text-5|$
-
$2$ _____ $\text-17$
-
$2$ _____ $|\text-17|$
-
$|\text-27|$ _____ $|\text-45|$
-
$|\text-27|$ _____ $\text-45$
Problem 4 (from Unit 7, Lesson 5)
Mai received and spent money in the following ways last month. For each example, write a signed number to represent the change in money from her perspective.
- Her grandmother gave her \$25 in a birthday card.
- She earned \$14 dollars babysitting.
- She spent \$10 on a ticket to the concert.
- She donated \$3 to a local charity
- She got \$2 interest on money that was in her savings account.
Problem 5 (from Unit 7, Lesson 1)
Here are the lowest temperatures recorded in the last 2 centuries for some US cities. Temperatures are in degrees Fahrenheit.
- Death Valley, CA was -45 in January of 1937.
- Danbury, CT was -37 in February of 1943.
- Monticello, FL was -2 in February of 1899.
- East Saint Louis, IL was -36 in January of 1999.
- Greenville, GA was -17 in January of 1940.
- Which of these states has the lowest record temperature?
- Which state has a lower record temperature, FL or GA?
- Which state has a lower record temperature, CT or IL?
- How many more degrees colder is the record temperature for GA than for FL?
Problem 6 (from Unit 5, Lesson 13)
Find the quotients.
- $0.024 \div 0.015$
- $0.24 \div 0.015$
- $0.024 \div 0.15$
- $24 \div 15$
Lesson 8
Problem 1
At the book sale, all books cost less than \$5.
- What is the most expensive a book could be?
- Write an inequality to represent costs of books at the sale.
- Draw a number line to represent the inequality.
Problem 2
Kiran started his homework before 7:00 p.m. and finished his homework after 8:00 p.m. Let $h$ represent the number of hours Kiran worked on his homework.
Decide if each statement it is definitely true, definitely not true, or possibly true. Explain your reasoning.
-
$h > 1$
-
$h > 2$
-
$h < 1$
-
$h < 2$
Problem 3 (from Unit 6, Lesson 14)
Consider a rectangular prism with length 4 and width and height $d$.
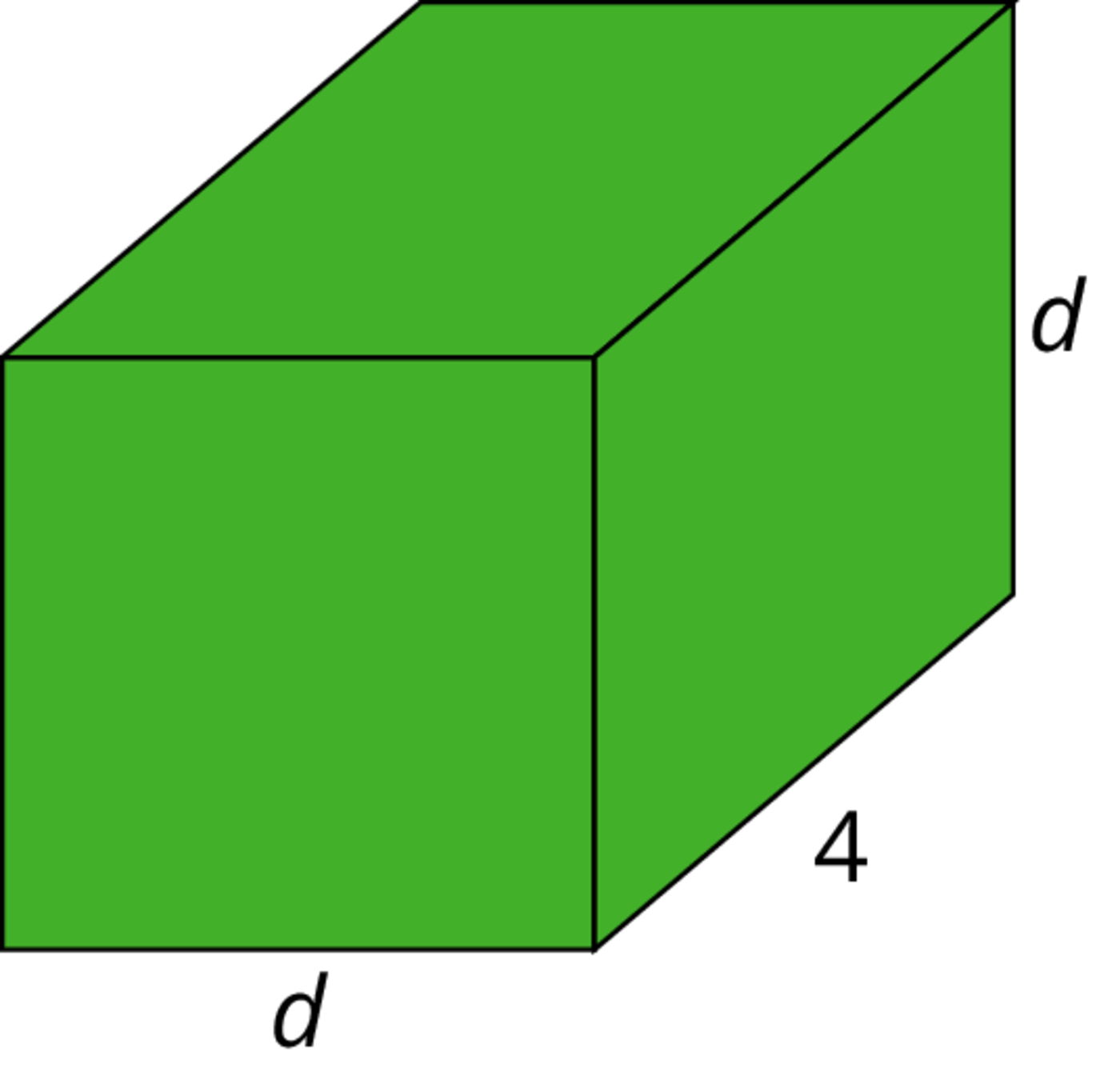
- Find an expression for the volume of the prism in terms of $d$.
- Compute the volume of the prism when $d=1$, when $d=2$, and when $d=\frac12$.
Problem 4 (from Unit 7, Lesson 7)
Match the mathematical statements with the statements written in English. All of these statements are true.
- $|\text-12| > \text-15$
- $\text-15 < \text-12$
- $|\text-15| > |\text-12|$
- $|\text-12| = 12$
- $12 > \text-12$
- $|12| = |\text-12|$
- The number -15 is further away from 0 than the number -12 on the number line.
- The number -12 is a distance of 12 units away from 0 on the number line.
- The distance between -12 and 0 on the number line is greater than -15.
- The numbers 12 and -12 are the same distance away from 0 on the number line.
- The number -15 is less than the number -12.
- The number 12 is greater than the number -12.
Problem 5 (from Unit 6, Lesson 11)
Here are five sums. Use the distributive property to write each sum as a product with two factors.
- $2a+7a$
- $5z-10$
- $c-2c^2$
- $r+r+r+r$
- $2x-\frac12$
Lesson 9
Problem 1
- Select all numbers that are solutions to the inequality $k > 5$.
- 4
- 5
- 6
- 5.2
- 5.01
- 0.5
- Draw a number line to represent this inequality.
Problem 2
A sign on the road says: “Speed limit, 60 miles per hour.”
- Let $s$ be the speed of a car. Write an inequality that matches the information on the sign.
- Draw a number line to represent the solutions to the inequality.
- Could 60 be a value of $s$? Explain your reasoning.
Problem 3
One day in Boston, MA, the high temperature was 60 degrees Fahrenheit, and the low temperature was 52 degrees.
- Write one or more inequalities to describe the temperatures $T$ that are between the high and low temperature on that day.
- Show the possible temperatures on a number line.
Problem 4 (from Unit 7, Lesson 7)
Select all the true statements.
-
$\text-5 < |\text-5|$
-
$|\text-6| < \text-5$
-
$|\text-6| < 3$
-
$4 < |\text-7|$
-
$|\text-7| < |\text-8|$
Problem 5 (from Unit 6, Lesson 15)
Match each equation to its solution.
- $x^4=81$
- $x^2=100$
- $x^3=64$
- $x^5=32$
- 2
- 3
- 4
- 10
Problem 6 (from Unit 3, Lesson 14)
-
The price of a cell phone is usually \$250. Elena’s mom buys one of these cell phones for \$150. What percentage of the usual price did she pay?
-
Elena’s dad buys another type of cell phone that also usually sells for \$250. He pays 75% of the usual price. How much did he pay?
Lesson 10
Problem 1
There is a closed carton of eggs in Mai's refrigerator. The carton contains $e$ eggs and it can hold 12 eggs.
-
What does the inequality $e < 12$ mean in this context?
-
What does the inequality $e > 0$ mean in this context?
-
What are some possible values of $e$ that will make both $e < 12$ and $e > 0$ true?
Problem 2
Here is a diagram of an unbalanced hanger.

- Write an inequality to represent the relationship of the weights. Use $s$ to represent the weight of the square in grams and $c$ to represent the weight of the circle in grams.
- One red circle weighs 12 grams. Write an inequality to represent the weight of one blue square.
- Could 0 be a value of $s$? Explain your reasoning.
Problem 3
Tyler has more than \$10. Elena has more money than Tyler. Mai has more money than Elena. Let $t$ be the amount of money that Tyler has, let $e$ be the amount of money that Elena has, and let $m$ be the amount of money that Mai has. Select all statements that are true:
- $t < j$
- $m > 10$
- $e > 10$
- $t > 10$
- $e > m$
- $t < e$
Problem 4 (from Unit 7, Lesson 8)
-
Jada is taller than Diego. Diego is 54 inches tall (4 feet, 6 inches). Write an inequality that compares Jada’s height in inches, $j$, to Diego’s height.
-
Jada is shorter than Elena. Elena is 5 feet tall. Write an inequality that compares Jada’s height in inches, $j$, to Elena’s height.
Problem 5 (from Unit 7, Lesson 3)
Which is greater, $\frac {\text{-}9}{20}$ or -0.5? Explain how you know. If you get stuck, consider plotting the numbers on a number line.
Problem 6 (from Unit 6, Lesson 13)
Select all the expressions that are equivalent to $\left(\frac{1}{2}\right)^3$.
- $\frac{1}{2} \boldcdot \frac{1}{2} \boldcdot \frac{1}{2}$
- $\frac{1}{2^3}$
- $\left(\frac{1}{3}\right)^2$
- $\frac{1}{6}$
- $\frac{1}{8}$
Lesson 11
Problem 1
-
Graph these points in a coordinate plane: $(\text-2,3)$, $ (2,3)$, $ (\text-2, \text-3)$, $(2, \text-3)$.
-
Connect all of the points. Describe the figure.
Problem 2
Write the coordinates of each point.

Problem 3
These three points form a horizontal line: $(\text-3.5, 4)$, $(0, 4)$, and $(6.2, 4)$. Name two additional points that fall on this line.
Problem 4 (from Unit 7, Lesson 2)
One night, it is $24^\circ\text{C}$ warmer in Tucson than it was in Minneapolis. If the temperatures in Tucson and Minneapolis are opposites, what is the temperature in Tucson?
-
$\text-24^\circ\text{C}$
-
$\text-12^\circ\text{C}$
-
$12^\circ\text{C}$
-
$24^\circ\text{C}$
Problem 5 (from Unit 6, Lesson 16)
Noah is helping his band sell boxes of chocolate to fund a field trip. Each box contains 20 bars and each bar sells for \$1.50.
- Complete the table for values of $m$.
row 1 boxes sold $(b)$ money collected $(m)$ row 2 1 row 3 2 row 4 3 row 5 4 row 6 5 row 7 6 row 8 7 row 9 8 - Write an equation for the amount of money, $m$, that will be collected if $b$ boxes of chocolate bars are sold. Which is the independent variable and which is the dependent variable in your equation?
- Write an equation for the number of boxes, $b$, that were sold if $m$ dollars were collected. Which is the independent variable and which is the dependent variable in your equation?
Problem 6 (from Unit 2, Lesson 9)
Lin ran 29 meters in 10 seconds. She ran at a constant speed.
- How far did Lin run every second?
- At this rate, how far can she run in 1 minute?
Lesson 12
Problem 1
Draw and label an appropriate pair of axes and plot the points.
$(\frac15, \frac45)$
$(\frac {\text{-}3}{5}, \frac25)$
$(\text-1 \frac15, \frac {\text{-}4}{5})$
$(\frac15, \frac {\text{-}3}{5})$
Problem 2
Diego was asked to plot these points: $(\text-50, 0)$, $(150, 100)$, $(200, \text-100)$, $(350, 50)$, $(\text-250, 0)$. What interval could he use for each axis? Explain your reasoning.
Problem 3
- Name 4 points that would form a square with the origin at its center.
- Graph these points to check if they form a square.
Problem 4 (from Unit 7, Lesson 5)
Which of the following changes would you represent using a negative number? Explain what a positive number would represent in that situation.
- A loss of 4 points
- A gain of 50 yards
- A loss of \$10
- An elevation above sea level
Problem 5 (from Unit 6, Lesson 16)
Jada is buying notebooks for school. The cost of each notebook is $1.75.
- Write an equation that shows the cost of Jada’s notebooks, $c$, in terms of the number of notebooks, $n$, that she buys.
- Which of the following could be points on the graph of your equation?
$(1.75, 1)$
$(2, 3.50)$
$(5, 8.75)$
$(17.50, 10)$
$(9, 15.35)$
Problem 6 (from Unit 5, Lesson 13)
A corn field has an area of 28.6 acres. It requires about 15,000,000 gallons of water. About how many gallons of water per acre is that?
- 5,000
- 50,000
- 500,000
- 5,000,000
Lesson 13
Problem 1
The elevation of a submarine is shown in the table. Draw and label coordinate axes with an appropriate scale and plot the points.
| time after noon (hours) | elevation (meters) | |
|---|---|---|
| row 1 | 0 | -567 |
| row 2 | 1 | -892 |
| row 3 | 2 | -1,606 |
| row 4 | 3 | -1,289 |
| row 5 | 4 | -990 |
| row 6 | 5 | -702 |
| row 7 | 6 | -365 |
Problem 2
The $x$-axis represents the number of hours before or after noon, and the $y$-axis represents the temperature in degrees Celsius.
-
At 9 a.m., it was below freezing. In what quadrant would this point be plotted?
-
At 11 a.m., it was $10^\circ \text{C}$. In what quadrant would this point be plotted?
-
Choose another time and temperature. Then tell the quadrant where the point should be plotted.
-
What does the point $(0, 0)$ represent in this context?
Problem 3 (from Unit 7, Lesson 8)
The inequalities $h > 42$ and $h< 60$ represent the height requirements for an amusement park ride, where $h$ represents a person's height in inches.
Write a sentence or draw a sign or that describes these rules as clearly as possible.
Problem 4 (from Unit 6, Lesson 4)
Solve each equation.
- $3a = 12$
- $b + 3.3 = 8.9$
- $1 = \frac{1}{4} c$
- $5\frac{1}{2} = d+ \frac{1}{4} $
- $2e = 6.4$
Lesson 14
Problem 1
Here are 4 points on a coordinate plane.

- Label each point with its coordinates.
- Plot a point that is 3 units from point $K$. Label it $P$.
- Plot a point that is 2 units from point $M$. Label it $W$.
Problem 2
Each set of points are connected to form a line segment. What is the length of each?
- A = $(3, 5)$ and B = $(3, 6)$
- C = $(\text-2, \text-3)$ and D = $(\text-2, \text-6)$
- E = $(\text-3, 1)$ and F = $(\text-3, \text-1)$
Problem 3
On the coordinate plane, plot four points that are each 3 units away from point $P=(\text-2, \text-1)$. Write the coordinates of each point.

Problem 4 (from Unit 6, Lesson 16)
Noah’s recipe for sparkling orange juice uses 4 liters of orange juice and 5 liters of soda water.
- Noah prepares large batches of sparkling orange juice for school parties. He usually knows the total number of liters, $t$, that he needs to prepare. Write an equation that shows how Noah can find $s$, the number of liters of soda water, if he knows $t$.
- Sometimes the school purchases a certain number, $j$, of liters of orange juice and Noah needs to figure out how much sparkling orange juice he can make. Write an equation that Noah can use to find $t$ if he knows $j$.
Problem 5 (from Unit 3, Lesson 4)
For a suitcase to be checked on a flight (instead of carried by hand), it can weigh at most 50 pounds. Andre’s suitcase weighs 23 kilograms. Can Andre check his suitcase? Explain or show your reasoning. (Note: 10 kilograms $\approx$ 22 pounds)
Lesson 15
Problem 1
The coordinates of a rectangle are $(3, 0)$, $(3, \text-5)$, $(\text-4, 0)$ and $(\text-4, \text-5)$
- What is the length and width of this rectangle?
- What is the perimeter of the rectangle?
- What is the area of the rectangle?
Problem 2
Draw a square with one vertex on the origin $(\text-3,5)$ and a perimeter of 20.
Problem 3
- Plot and connect the following points to form a polygon.
$(\text-3, 2), (2, 2), (2, \text-4), (\text-1, \text-4), (\text-1, \text-2), (\text-3, \text-2), (\text-3, 2)$

-
Find the perimeter of the polygon.
Problem 4 (from Unit 6, Lesson 4)
For each situation, select all the equations that represent it. Choose one equation and solve it.
-
Jada’s cat weighs 3.45 kg. Andre’s cat weighs 1.2 kg more than Jada’s cat. How much does Andre’s cat weigh?
$x = 3.45 + 1.2$
$x = 3.45 - 1.2$
$x +1.2 = 3.45$
$x-1.2=3.45$
-
Apples cost \$1.60 per pound at the farmer’s market. They cost 1.5 times as much at the grocery store. How much do the apples cost per pound at the grocery store?
$y = (1.5) \boldcdot (1.60)$
$y = 1.60 \div 1.5$
(1.5)y = 1.60
$\frac{y}{1.5} = 1.60$
Lesson 16
Problem 1
A teacher is making gift bags. Each bag is to be filled with pencils and stickers. The teacher has 24 pencils and 36 stickers to use. Each bag will have the same number of each item, with no items left over.
For example, she could make 2 bags with 12 pencils and 18 stickers each.
What are the other possibilities? Explain or show your reasoning.
Problem 2
-
List all the factors of 42.
-
What is the greatest common factor of 42 and 15?
-
What is the greatest common factor of 42 and 50?
Problem 3
A school chorus has 90 sixth-grade students and 75 seventh-grade students. The music director wants to make groups of performers, with the same combination of sixth- and seventh-grade students in each group. She wants to form as many groups as possible.
-
What is the largest number of groups that could be formed? Explain or show your reasoning.
-
If that many groups are formed, how many students of each grade level would be in each group?
Problem 4 (from Unit 7, Lesson 13)
Here are some bank transactions from a bank account last week. Which transactions represent negative values?
Monday: \$650 paycheck deposited
Tuesday: \$40 withdrawal from the ATM at the gas pump
Wednesday: \$20 credit for returned merchandise
Thursday: \$125 deducted for cell phone charges
Friday: \$45 check written to pay for book order
Saturday: \$80 withdrawal for weekend spending money
Sunday: \$10 cash-back reward deposited from a credit card company
Problem 5 (from Unit 4, Lesson 11)
Find the quotients.
- $\frac{1}{7} \div \frac{1}{8}$
- $\frac{12}{5} \div \frac{6}{5}$
- $\frac{1}{10} \div 10$
- $\frac{9}{10} \div \frac{10}{9}$
Problem 6 (from Unit 2, Lesson 9)
An elephant can travel at a constant speed of 25 miles per hour, while a giraffe can travel at a constant speed of 16 miles in $\frac12$ hour.
- Which animal runs faster? Explain your reasoning.
- How far can each animal run in 3 hours?
Lesson 17
Problem 1
- A green light blinks every 4 seconds and a yellow light blinks every 5 seconds. When will both lights blink at the same time?
- A red light blinks every 12 seconds and a blue light blinks every 9 seconds. When will both lights blink at the same time?
- Explain how to determine when 2 lights blink together.
Problem 2
- List all multiples of 10 up to 100.
- List all multiples of 15 up to 100.
- What is the least common multiple of 10 and 15?
Problem 3
Cups are sold in packages of 8. Napkins are sold in packages of 12.
- What is the fewest number of packages of cups and the fewest number of packages of napkins that can be purchased so there will be the same number of cups as napkins?
- How many sets of plates and napkins will there be?
Problem 4 (from Unit 7, Lesson 14)
Rectangle ABCD is drawn on a coordinate plane. A = $(\text-6, 9)$ and B = $(5, 9)$.
What could be the locations of points C and D?
Problem 5 (from Unit 3, Lesson 14)
A school wants to raise \$2,500 to support its music program.
-
If it has met 20% of its goal so far, how much money has it raised?
-
If it raises 175% of its goal, how much money will the music program receive? Show your reasoning.
Lesson 18
Problem 1
Mai, Clare, and Noah are making signs to advertise the school dance. It takes Mai 6 minutes to complete a sign, it takes Clare 8 minutes to complete a sign, and it takes Noah 5 minutes to complete a sign. They keep working at the same rate for a half hour.
- Will Mai and Clare complete a sign at the same time? Explain your reasoning.
- Will Mai and Noah complete a sign at the same time? Explain your reasoning.
- Will Clare and Noah complete a sign at the same time? Explain your reasoning
- Will all three students complete a sign at the same time? Explain your reasoning
Problem 2 (from Unit 7, Lesson 16)
Diego has 48 chocolate chip cookies, 64 vanilla cookies, and 100 raisin cookies for a bake sale. He wants to make bags that have all three cookie flavors and the same number of each flavor per bag.
- How many bags can he make without having any cookies left over?
- Find the another solution to this problem.
Problem 3
- Find the product of 12 and 8.
- Find the greatest common factor of 12 and 8.
- Find the least common multiple of 12 and 8.
- Find the product of the greatest common factor and the least common multiple of 12 and 8.
- What do you notice about the answers to question 1 and question 4?
- Choose 2 other numbers and repeat steps 1-5. Do you get the same results?
Problem 4 (from Unit 7, Lesson 11)
- Given the point $(5.5, \text-7)$, name a second point so that the two points form a vertical segment.
- Given the point $(3, 3.5)$, name a second point so that the two points form a horizontal segment.
Problem 5 (from Unit 6, Lesson 9)
Find the value of each expression mentally.
- $\frac12\boldcdot 37-\frac12 \boldcdot 7$
- $3.5\boldcdot 40+3.5\boldcdot 60$
- $999\boldcdot 5$