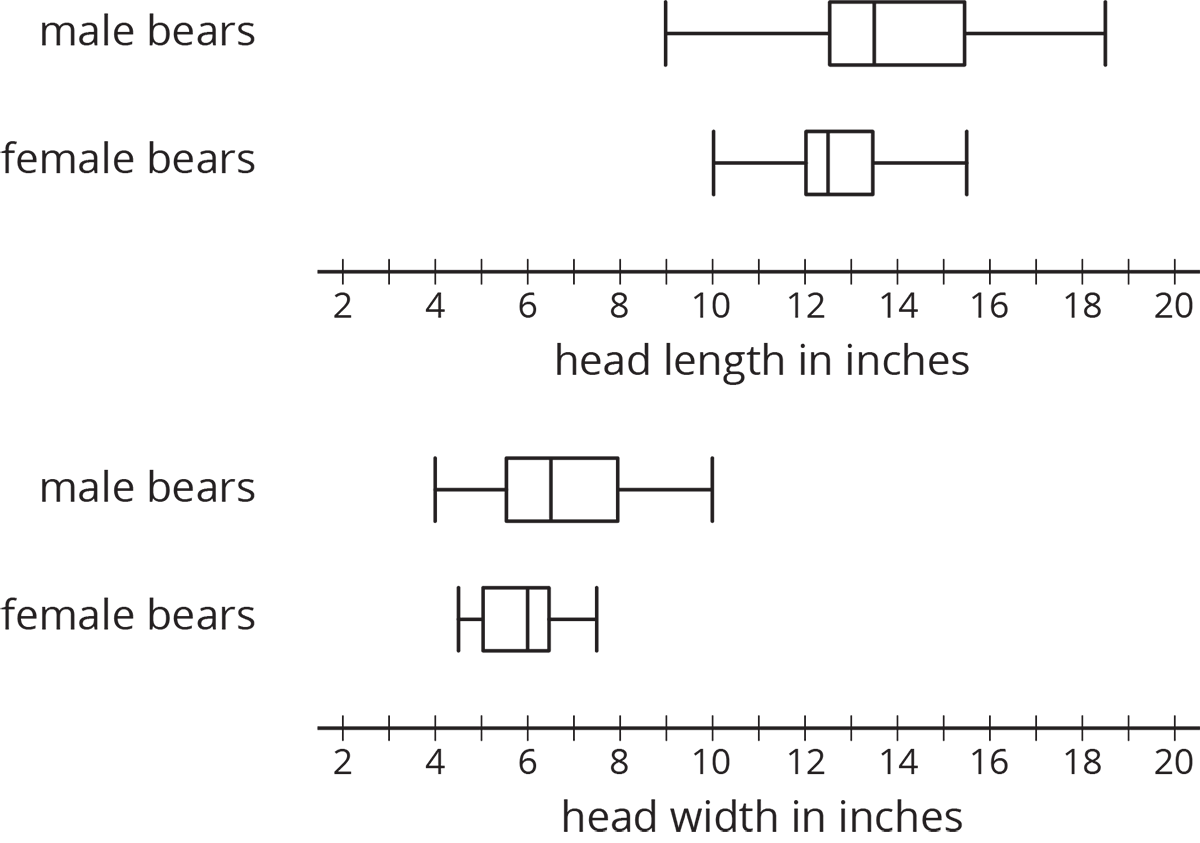
The dot plot shows the distribution of 30 cookie weights in grams.
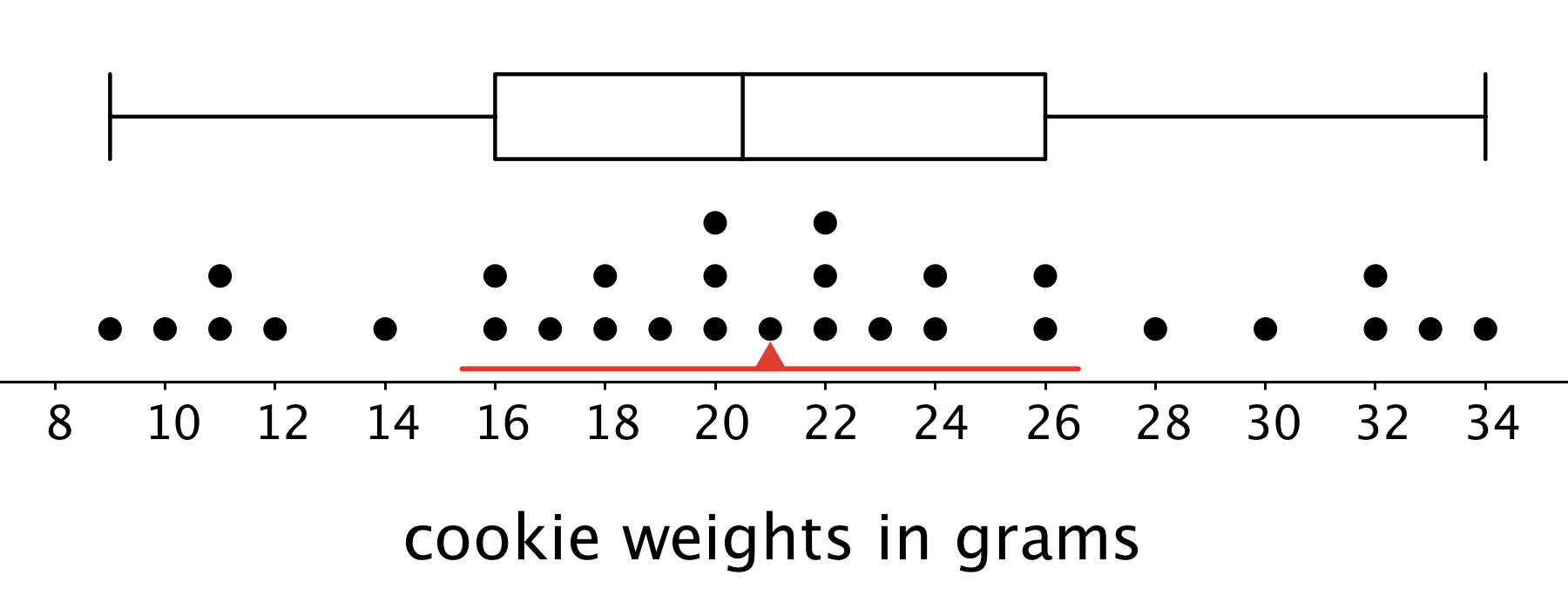
The mean cookie weight, marked by the triangle, is 21 grams. This tells us that if the weights of all of the cookies were redistributed so they all had the same weight, each cookie would weigh 21 grams. The MAD is 5.6 grams, which suggests that a cookie typically weighs between 15.4 grams and 26.6 grams.
The box plot for the same data set is shown above the dot plot. The median shows that half of the weights are greater than or equal to 20.5 grams, and half are less than or equal to 20.5 grams. The box shows that the IQR is 10 and that the middle half of the cookies weigh between 16 and 26 grams.
In this case, the median weight is very close to the mean weight, and the IQR is about twice the MAD. This tells us that the two pairs of measures of center and spread are very similar.
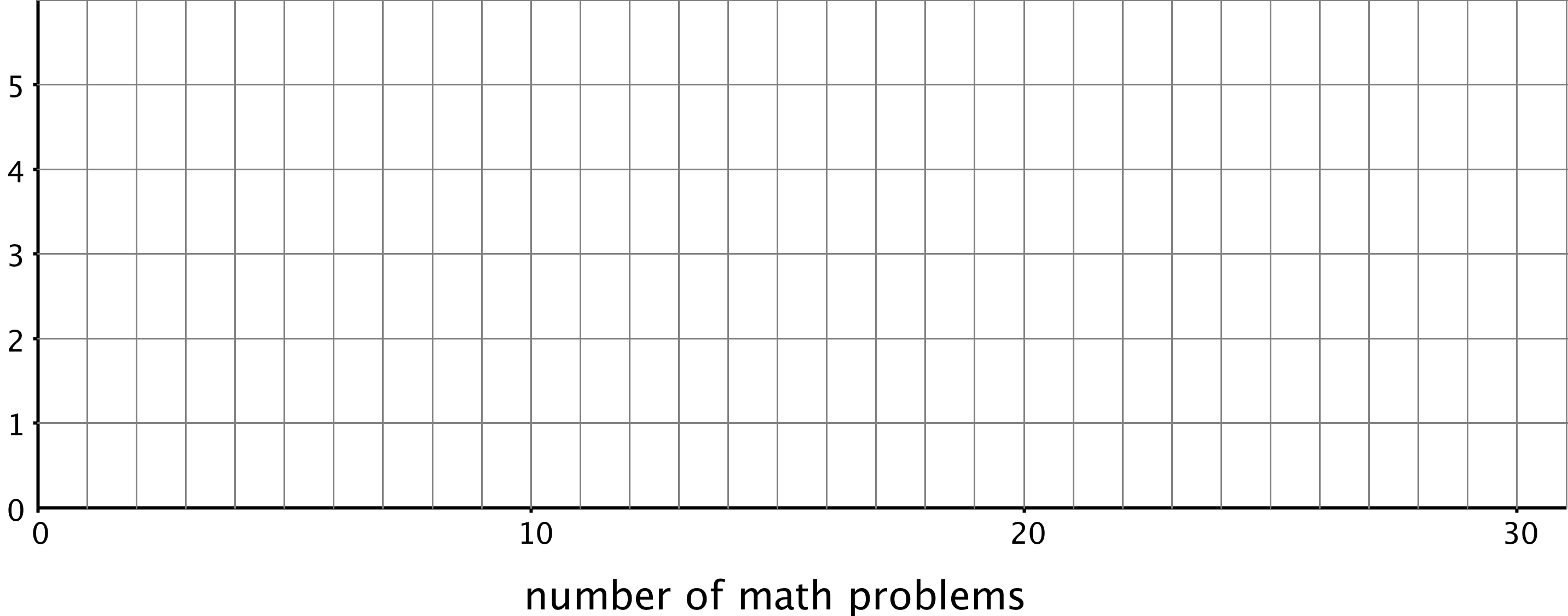
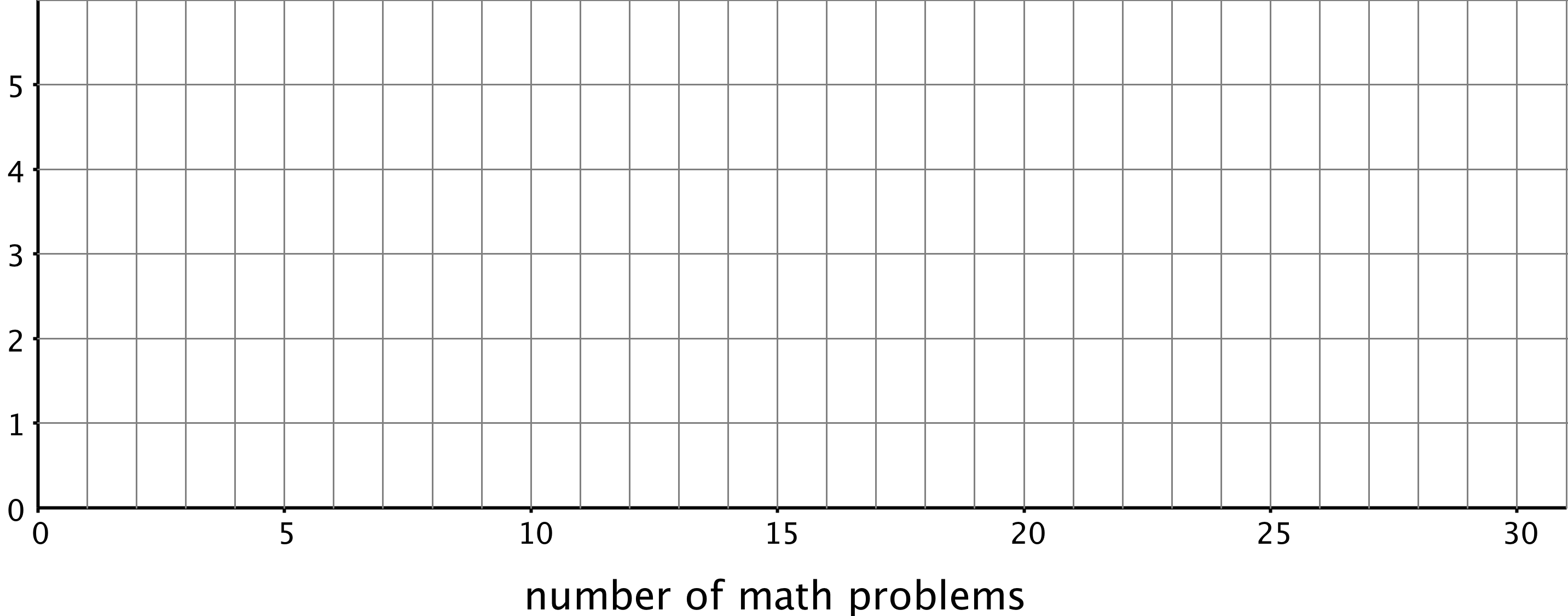
Now let’s look at another example of 30 different cookies.

Here the mean is 21 grams, and the MAD is 3.4 grams. This suggests that a cookie typically weighs between 17.6 and 24.4 grams. The median cookie weight is 23 grams, and the box plot shows that the middle half of the data are between 20 and 24 grams. These two pairs of measures paint very different pictures of the variability of the cookie weights.
The median (23 grams) is closer to the middle of the big cluster of values. If we were to ignore the smaller cookies, the median and IQR would give a more accurate picture of how much a cookie typically weighs.
When a distribution is not symmetrical, the median and IQR are often better measures of center and spread than the mean and MAD. However the decision on which pair of measures to use depends on what we want to know about the group we are investigating.