The side length of each square is 1 centimeter. The area of the shaded region A is 8 square centimeters. The area of shaded region B is $\frac12$ square centimeters.
Grade 6 Glossary
absolute value
The absolute value of a number is its distance from 0 on the number line.
area
The area of a two-dimensional region, measured in square units, is the number of unit squares that cover the region without gaps or overlaps.
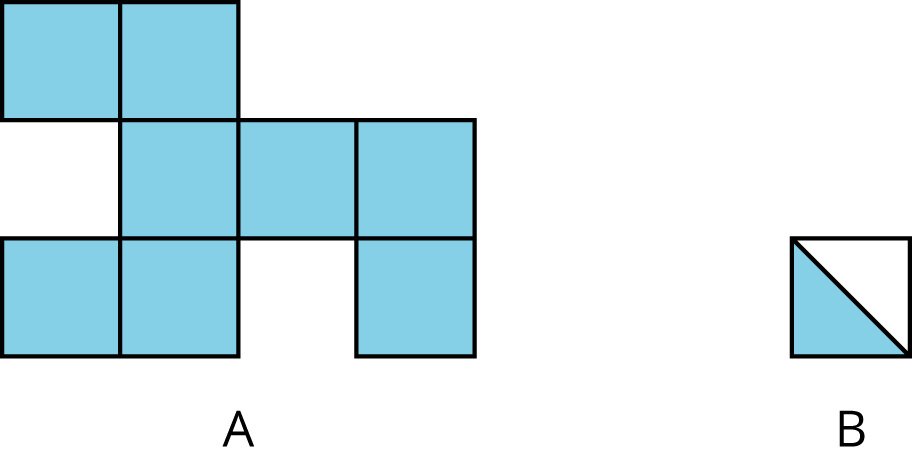
average
The average, or mean, of a data set is the value you get by adding up all of the values in the set and dividing by the number of values in the set.
base/height of a parallelogram
Any of the four sides of a parallelogram can be chosen as a base. The term base can also refer to the length of this side. Once we have chosen a base, then a perpendicular segment from a point on the base of a parallelogram to the opposite side will always have the same length. We call that value the height.
base/height of a triangle
Any of the three sides of a triangle can be chosen as a base. The term base can also refer to the length of this side. Once we have chosen a base, the corresponding height is the length of a perpendicular segment from the base to the vertex opposite it. The opposite vertex is the vertex that is not an endpoint of the base.
box plot
A box plot is a representation of a data set that shows the five-number summary. It shows the first quartile (Q1) and the third quartile (Q3) as the left and right sides of a rectangle or a box. The median (Q2) is shown as a vertical segment inside the box. The box represents the middle half of the data. Its width is the interquartile range. The "whiskers" on the sides represent the bottom quarter and top quarter. They always extend to the minimum and maximum values of the data set.
categorical data
Categorical data are data where the values are categories. For example, the breeds of 10 different dogs are categorical data. Another example is the colors of 100 different flowers.
center
For a symmetrical or almost symmetrical data distribution, the center is the value around which the distribution is symmetrical. We also use the idea of center for distributions that are not symmetrical (for example the mean or median).
coefficient
In an algebraic expression, the coefficient of a variable is the constant the variable is multiplied by. If the variable appears by itself then it is regarded as being multiplied by 1 and the coefficient is 1.
common factor
A common factor of two whole numbers is a factor that they have in common. For example, 5 is a common factor of 15 and 20.
common multiple
A common multiple for two whole numbers is a number that is a multiple of both numbers. For example, 20 is a multiple of 2 and a multiple of 5, so 20 is a common multiple of 2 and 5.
compose/decompose
Compose means “put together” and decompose means “take apart.” We use the word “compose” to describe putting several geometric figures together to make a new figure.
cube of a number / cubing a number
An expression with an exponent of 3 is sometimes called a cube. The reason $s^3$ is called the cube of $s$ is that a cube whose edge has length $s$ has volume $s^3$.
dependent variable
A variable representing the output of a function.
distribution
For a numerical or categorical data set, the distribution tells you how many of each value or each category there are in the data set.
dot plot
A dot plot (sometimes called a line plot) is a way to represent the distribution of a numerical data set. For example, here is a dot plot showing the distribution of dog weights for 10 dogs:
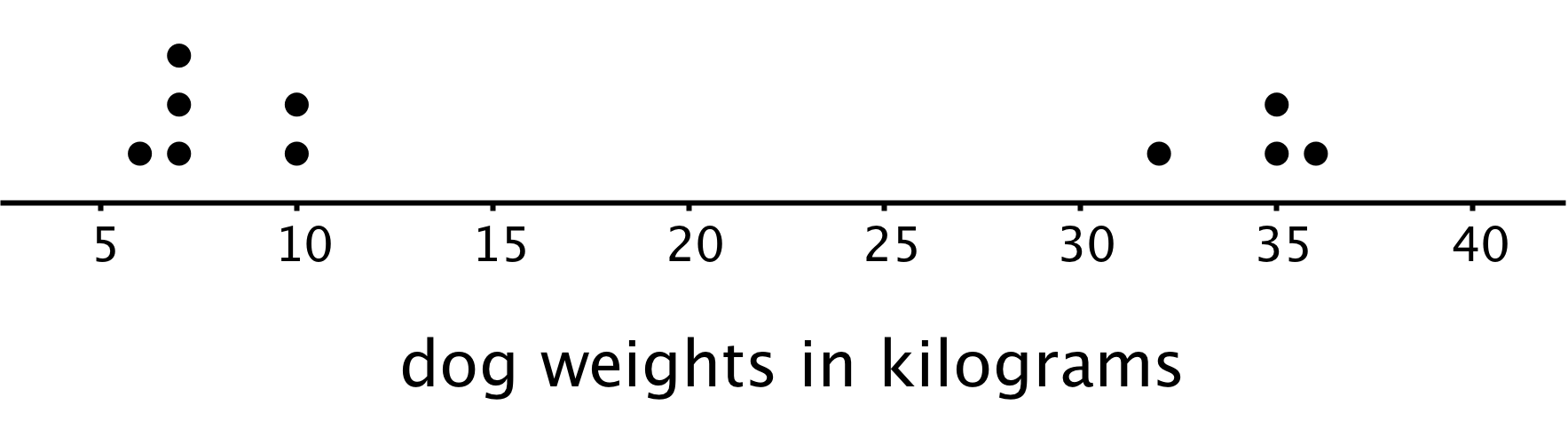
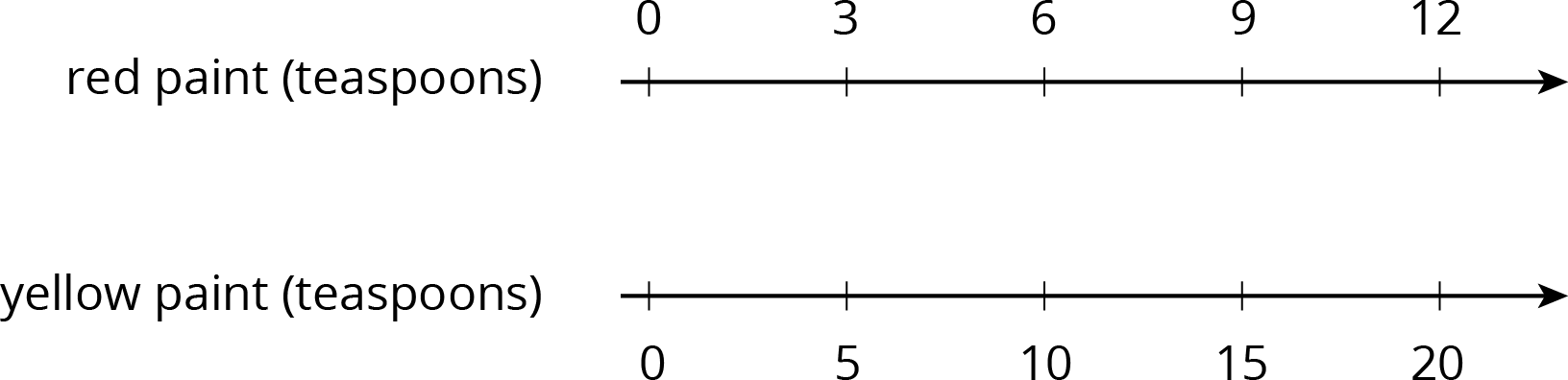
double number line diagram
A double number line diagram is a pair of parallel number lines with the numbers 0 aligned. Each number line is marked in equal increments and numbered. The tick marks are aligned, but the numbers on the two lines are often different. A pair of aligned numbers on the diagram represents a ratio that is equivalent to every other pair of aligned numbers on the diagram.
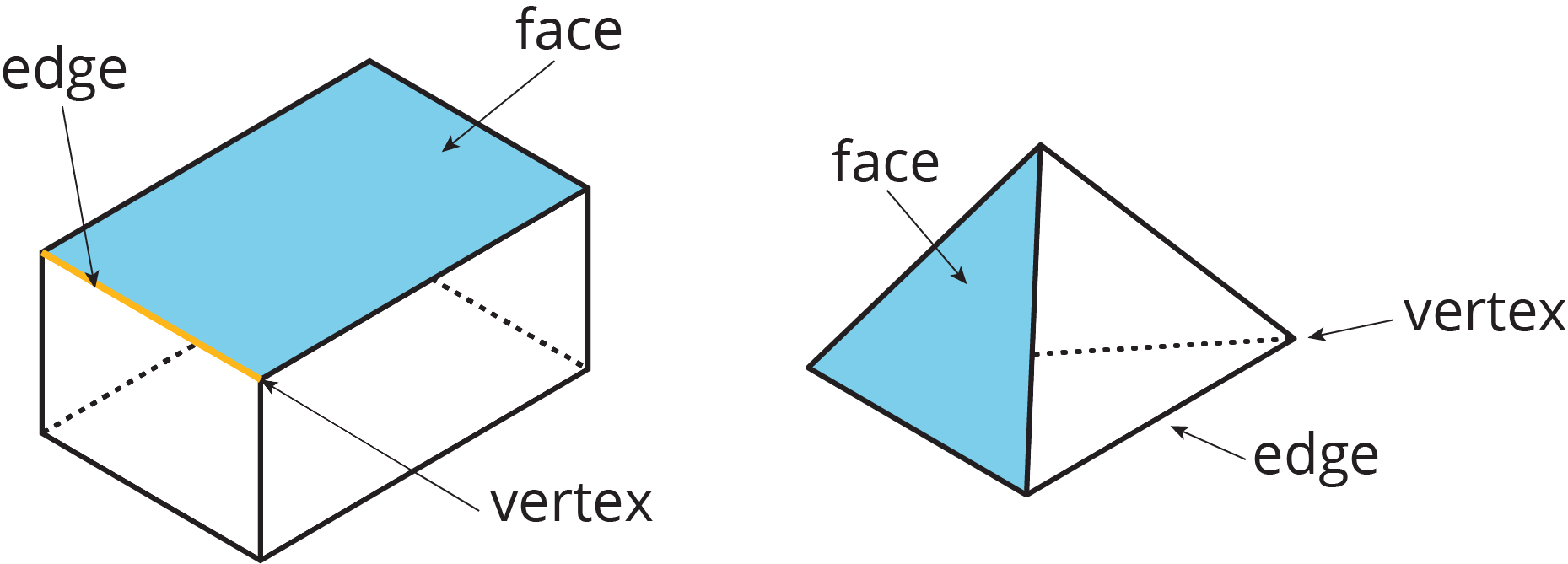
edge
A line segment in a polygon is called an edge (it is also called a side). A line segment where two faces meet in a polyhedron is also called an edge.
equivalent expressions
Expressions that are always equal for the same value of their variable are called equivalent expressions.
equivalent ratios
Two ratios $a:b$ and $c:d$ are equivalent ratios if there is a number $s$ that you can multiply both $a$ and $b$ by to get $c$ and $d$ (respectively). In other words, $a\boldcdot s = c$ and $b \boldcdot s = d$.
exponent
When we write an expression like $7^n$, we call $n$ the exponent.
face
Any flat surface on a three-dimensional figure is a face.
frequency
In statistics, the frequency of a particular data value is the number of times that value occurs in a data set. When that number is expressed as a fraction of the total number of data values, then it is called the relative frequency.
greatest common factor
The greatest common factor (sometimes written as GCF) of two whole numbers is the greatest of all of the common factors. For example, 15 is the greatest common factor for 45 and 60.
histogram
A histogram is a way of representing a numerical data set by grouping the data into bins and showing how many values are in each bin with a vertical bar.
independent variable
A variable representing the input of a function.
interquartile range (IQR)
The interquartile range of a data set is a measure of spread of its distribution. It is the difference between the third quartile (Q3) and the first quartile (Q1).
least common multiple
The least common multiple (sometimes written as LCM) of two whole numbers is the smallest multiple they have in common. For example, 30 is the least common multiple of 6 and 10.
long division
Long division is an algorithm for finding the quotient of two numbers expressed in decimal form. It works by building up the quotient one digit at a time, from left to right. Each time you get a new digit, you multiply the divisor by the corresponding base ten value and subtract that from the dividend.
Using long division we see that $513 \div 4 = 128 \frac14$. We can also write this as $513 = 128 \times 4 + 1$.
$$ \require{enclose} \begin{array}{r} 128 \\[-3pt] 4 \enclose{longdiv}{513}\kern-.2ex \\[-3pt] \underline{4{00}} \\[-3pt] 113 \\[-3pt] \underline{\phantom{0}8{0}} \\[-3pt] \phantom{0}33 \\[-3pt] \underline{\phantom{0}32} \\[-3pt] \phantom{00}1 \end{array} $$
mean
The mean, or average, of a data set is the value you get by adding up all of the values in the set and dividing by the number of values in the set.
mean absolute deviation (MAD)
The mean absolute deviation measures the spread in a distribution. It is the mean of the distances of the data points from the mean of the distribution. (It is called mean absolute deviation because the distance of a data point from the mean is the absolute value of its deviation from the mean.)
measure of center
A measure of center for a data distribution is a number that can be thought of as the middle or typical value of the distribution.
median
The median of a data set is the middle value when the data values are listed in order. If the number of values is even, it is the mean of the two middle values.
meters per second
A unit to measure speed that tells you how many meters an object travels in one second.
negative number
A negative number is any number that is less than zero. On a number line, negative numbers are always on the opposite side of 0 as 1. If a number line is drawn horizontally, the negative numbers are usually to the left of zero.

If a number line is drawn vertically, then the negative numbers are usually below zero, like most thermometers or on the vertical axis in the coordinate plane.
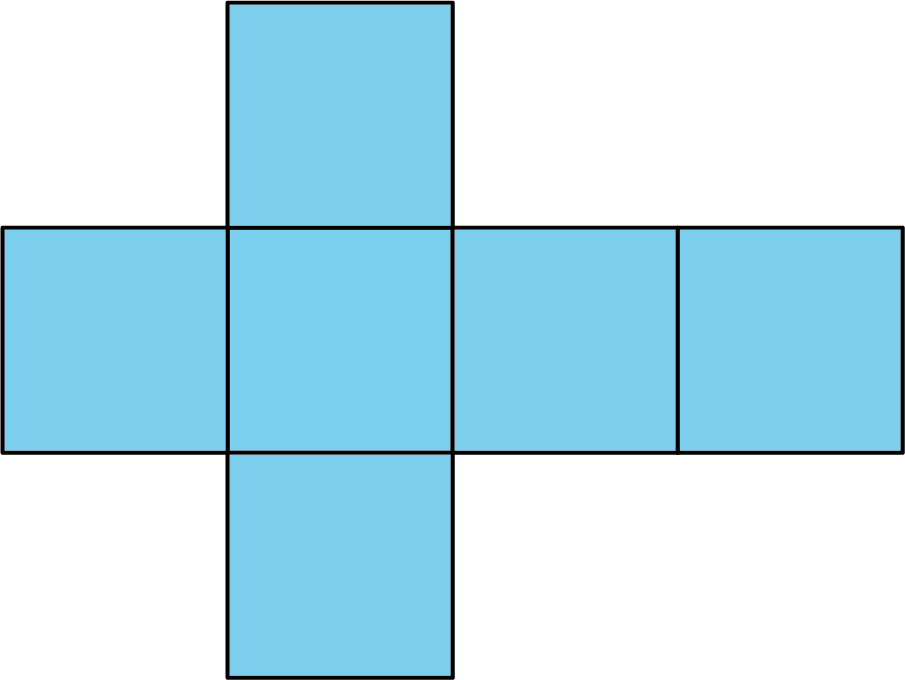
net
A net is a two-dimensional representation of a polyhedron. It can be cut out and folded to make a model of the polyhedron.
Here is a net for a cube.
numerical data
Numerical data, also called measurement or quantitative data, are data where the values are numbers, measurements, or quantities. For example, the weights of 10 different dogs are numerical data.
opposite
Two numbers are opposites of each other if they are the same distance from 0 on the number line, but on opposite sides.
opposite vertex
When you choose a side to be the base in a triangle, the vertex that is not an endpoint of the base is the opposite vertex.
Point $A$ is the opposite vertex to the base $\overline{BC}$

pace
Pace is an attribute that tells you how fast or slow an object is moving. A greater pace means the object is moving more slowly. Pace is measured in units like seconds per meter, hours per miles, and minutes per kilometer.
parallelogram
A parallelogram is a four-sided polygon with two pairs of parallel sides.
per
The word per means “for each.” For example: he paid \$5 for each ticket, so the cost was \$5 per ticket.
percent
The word percent means “per 100” or “for each 100” and is usually written symbolically like this: %.
percentage
A percentage is a quantity described by a rate per 100.
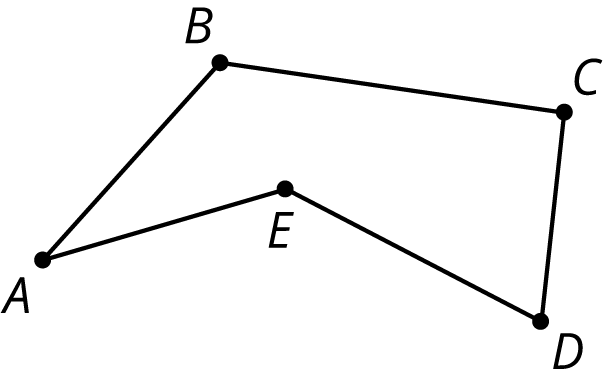
polygon
A polygon is a two-dimensional figure composed of a sequence of straight line segments, connected end-to-end, with the last one connecting back to the first. We call the line segments the edges or sides of the polygon. We call a point where the edges connect a vertex. The edges of a polygon never cross each other.
The plural of vertex is vertices. A polygon always encloses a two-dimensional region.
Here is a polygon with five vertices $A$, $B$, $C$, $D$, and $E$ and five edges (or sides): $\overline{AB}$, $\overline{BC}$, $\overline{CD}$, $\overline{DE}$, and $\overline{EA}$.
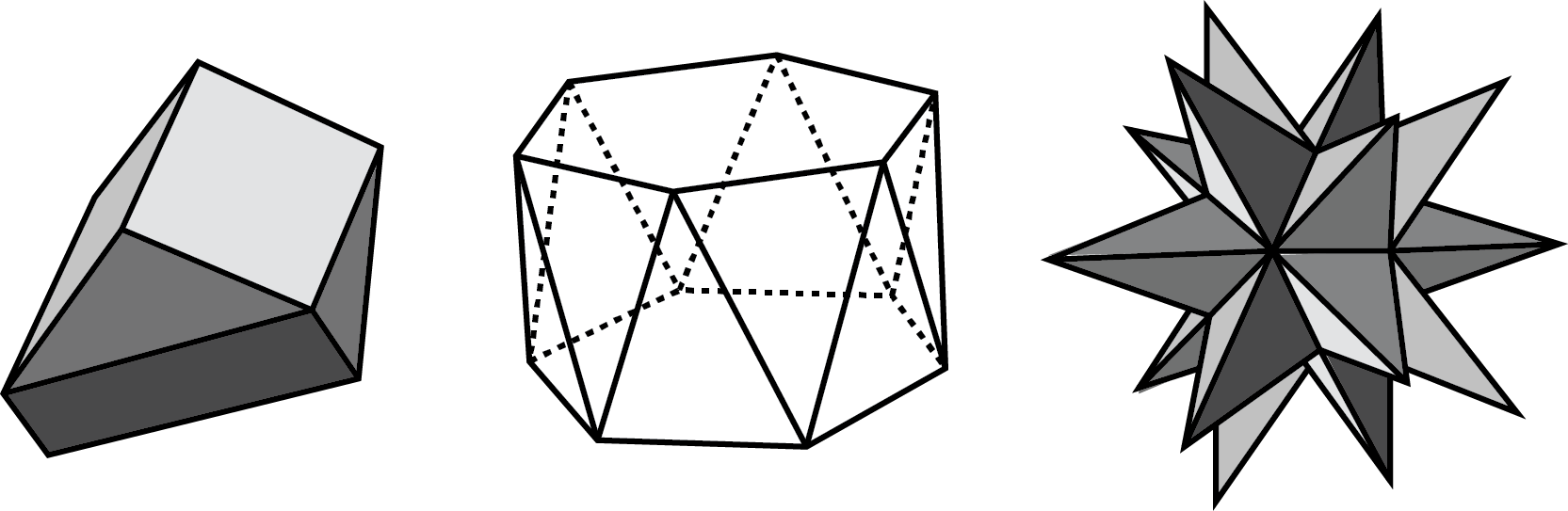
polyhedron (polyhedra)
A polyhedron is a three-dimensional figure with faces that are polygonal regions (filled-in polygons). Each face meets one and only one other face along a complete edge. The points where edges meet are called vertices. The plural of polyhedron is polyhedra.
A polyhedron always encloses a three-dimensional region. Here are some drawings of polyhedra.
positive number
A positive number is any number that is greater than zero. On a number line, positive numbers are always on the same side of 0 as 1. If a number line is drawn horizontally, the positive numbers are usually to the right of zero.

If a number line is drawn vertically, then the positive numbers are usually above zero, like most thermometers or on the vertical axis in the coordinate plane.
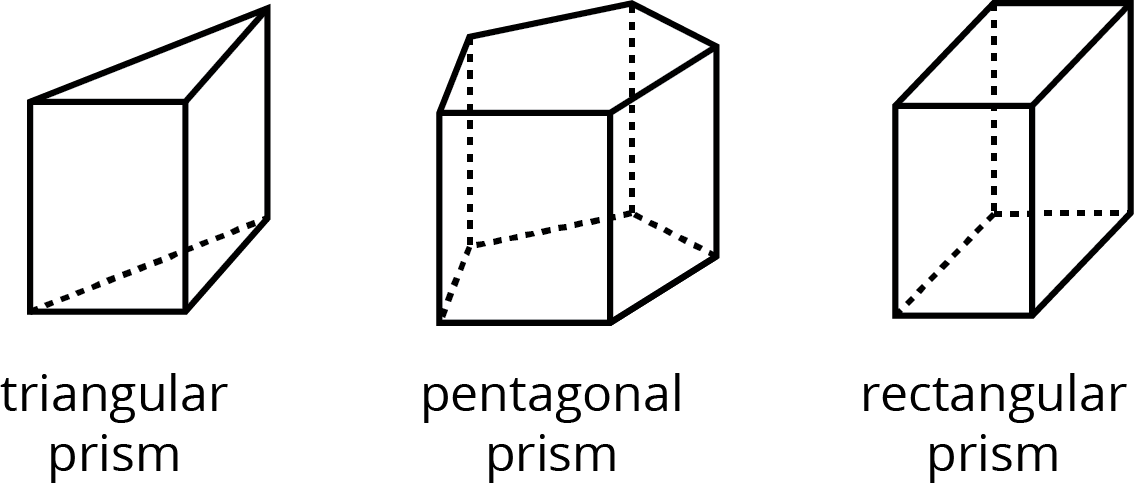
prism
A prism is a type of polyhedron with two parallel faces that are identical copies of each other (called bases) connected by rectangles.
A prism is named for the shape of its bases; for example, if its base is a pentagon, then it is called a “pentagonal prism.”
Here are some drawings of some prisms.
pyramid
A pyramid is a type of polyhedron that has one special face called the base. All of the other faces are triangles that all meet at a single vertex. A pyramid is named for the shape of its base; for example, if its base is a pentagon, then it is called a “pentagonal pyramid.”
quadrant
When axes extend in both positive and negative directions, the coordinate plane is divided into 4 regions called quadrants. The quadrants are numbered with Roman numerals, with quadrant I in the upper right, quadrant II in the upper left, quadrant III in the lower left, and quadrant IV in the lower right.
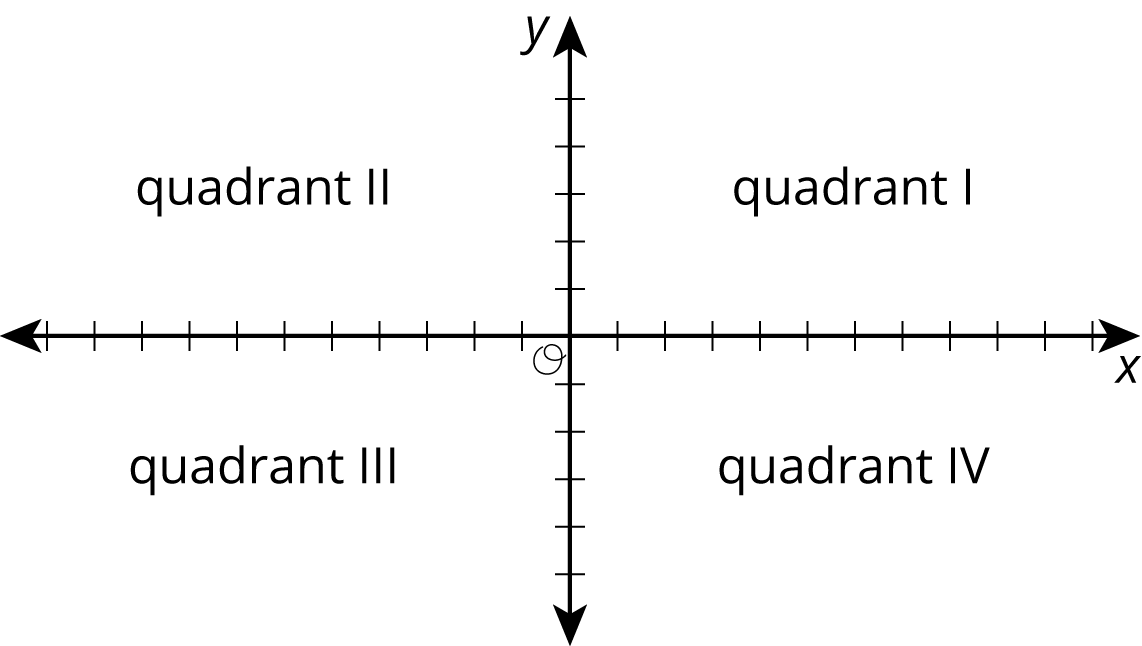
quadrilateral
A quadrilateral is a four-sided polygon.
quartile
The quartiles for a data set are three numbers that divide the data set into fourths. The median divides the set into two halves, and the first quartile (Q1) is the median of the lower half. The second quartile (Q2) is the median itself, and the third quartile (Q3) is the median of the upper half.
range
The range of a data set is the difference between the maximum and the minimum.
ratio
A ratio associates two or more quantities. Ratios can be described in words such as “3 to 2” and “3 for every 2” and “3 out of every 5” and “3 parts to 2 parts.” We write ratios with symbols like this: $3 : 2$.
rational number
A rational number is a fraction or the opposite of a fraction. Remember that a fraction is a point on the number line that you get by dividing the unit interval into $b$ equal parts and finding the point that is $a$ of them from 0. We can always write a fraction in the form $\frac{a}{b}$ where $a$ and $b$ are whole numbers, with $b$ not equal to 0, but there are other ways to write them. For example, 0.7 is a fraction because it is the point on the number line you get by dividing the unit interval into 10 equal parts and finding the point that is 7 of those parts away from 0. We can also write this number as $\frac{7}{10}$.
rearrange
When we decompose a figure into pieces and put them back together in a different way, we are rearranging the pieces.
region
Examples of two-dimensional regions include the interior of a circle or the interior of a polygon.
Here are two examples of two-dimensional regions. Area is a measure of two-dimensional regions.

Examples of a three-dimensional region include the interior of a sphere or the interior of a cube.
same rate
In two situations involving ratios of the same two quantities, if the ratio of the quantities in one situation is equivalent to the ratio of the quantities in the other situation then we say the two situations involve the same rate.
side
A line segment in a polygon is called a side (it is also called an edge).
Sometimes the faces of a polyhedron are called its sides.
sign
The sign of a nonzero number is either positive or negative.
solution to an equation
A solution to an equation with a variable in it is a number that can be used in place of the variable to make the equation true.
solution to an inequality
A solution to an inequality is a value of the variable that makes the inequality true. For example, $x = \text-3$ is a solution to the inequality $x < \text-1$, but $x = 3$ is not a solution.
speed
Speed is an attribute that tells you how fast or slow an object is moving. A greater speed means the object is moving faster. Speed is measured in units of distance per unit of time like meters per second, miles per hour, and kilometers per second.
spread
The spread of a data set tells you how spread out the data values are.
square of a number / squaring a number
An expression with an exponent of 2 is sometimes called a square. The reason $s^2$ is called the square of $s$ is that a square whose edge has length $s$ has area $s^2$.
statistical question
A statistical question is a question that can only be answered by using data and where we expect the data to have variability.
surface area
The surface area (in square units) is the number of unit squares it takes to cover all the surfaces of a three-dimensional figure without gaps or overlaps.
table
A table is a way to organize information. Each rectangle in the table is called a cell. Each horizontal set of entries is called a row, and each vertical set of entries is called a column. The first row in a table often contains headers to explain what information is in each column.
This table shows the tail-lengths of three different pets. It has four rows and two columns.
The first cell in each column tells you what kind of information is in that column.
| pet | tail length (inches) |
|---|---|
| dog | 22 |
| cat | 12 |
| mouse | 2 |
tape diagram
A tape diagram can be used to represent a ratio between two quantities measured in the same units.
The tape diagram shows a ratio of 30 gallons of yellow paint to 50 gallons of blue paint.
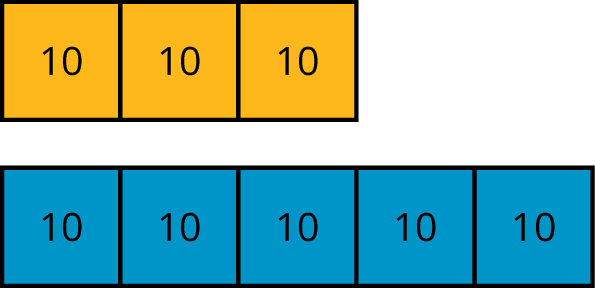
A tape diagram is composed of one or more rectangles that are partitioned into equal parts. Each part represents a value. It can be any value, as long as the same value is used throughout.
unit price
The unit price is the cost for one item or one unit of measure.
unit rate
A unit rate tells how many of one quantity there are per unit of another quantity.
variability
Variability is the tendency of a data set to have different data values.
variable
A variable is a letter in an equation.
vertex (vertices)
A vertex is a point where two edges meet in a polygon or a polyhedron.