Proportional Relationships with Fractions
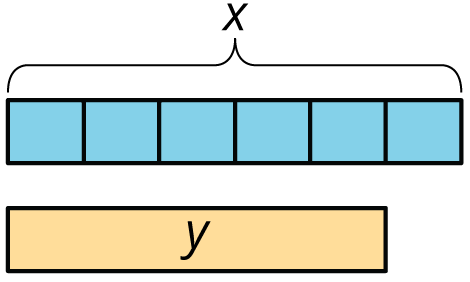
This week your student is learning about proportional relationships that involve fractions and decimals. For example, a baker decides to start using $\frac16$ less than the amount of sugar called for in each recipe. If the recipe calls for 2 cups of sugar, the baker will leave out $\frac16 \boldcdot 2$, or $\frac13$ cup of sugar. That means the baker will only use $2 - \frac13$, or $1\frac23$ cups of sugar.
| amount of sugar in the recipe ($x$) | amount of sugar the baker uses ($y$) | |
|---|---|---|
| row 1 | 1 cup | $\frac56$ cup |
| row 2 | $1\frac12$ cups | $1\frac14$ cups |
| row 3 | 2 cups | $1\frac23$ cups |
The amount of sugar the baker actually uses, $y$, is proportional to the amount of sugar called for in the recipe, $x$. The constant of proportionality is $\frac56$.
$y = x - \frac16 x$
$y = (1 - \frac16) x$
$y = \frac56 x$
Another way to write this equation is $y = 0.8\overline{3}x$. The line above the 3 tells us that if we use long division to divide $5 \div 6$, we will keep getting the answer 3 over and over. This is an example of a repeating decimal.
Here is a task to try with your student:
The baker also decides to start using $\frac16$ more than the amount of liquid called for in each recipe.
- How much of each ingredient will the baker use if the recipe calls for:
- $1\frac12$ cups of milk?
- 3 tablespoons of oil?
- What is the constant of proportionality for the relationship between the amount of liquid called for in the recipe and the amount this baker uses?
Solution:
-
- $1\frac34$ cups.
- $3\frac12$ tablespoons.
- $\frac76, 1.1\overline{6}$, or equivalent.
Percent Increase and Decrease
This week, your student is learning to describe increases and decreases as a percentage of the starting amount. For example, two different school clubs can gain the same number of students, but have different percent increases.
The cooking club had 50 students. Then they gained 6 students.
This is a 12% increase, because $6 \div 50 = 0.12$.
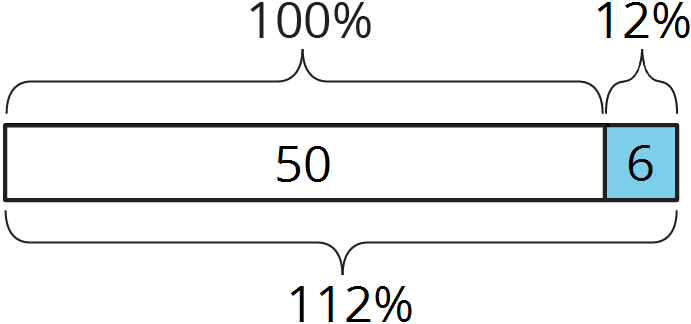
They now have 56 students, which is 112% of the starting amount.
$1.12 \boldcdot 50 = 56$
The computer club had 8 students. Then they gained 6 students.
This is a 75% increase, because $6 \div 8 = 0.75$.
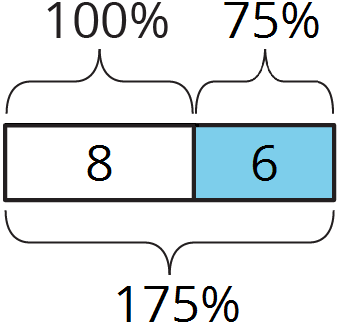
They now have 14 students, which is 175% of the starting amount.
$1.75 \boldcdot 8 = 14$
Here is a task to try with your student:
The photography club had 20 students. Then the number of students increased by 35%. How many students are in the photography club now?
Solution:
27 students. Possible strategies:
- The club gained 7 new students, because $0.35 \boldcdot 20 = 7$. The club now has 27 students, because $20 + 7 = 27$.
- The club now has 135% as many students as they started with, because $100 + 35 = 135$. That means they have 27 students, because $1.35 \boldcdot 20 = 27$.
Applying Percentages
This week, your student is learning about real-world situations that use percent increase and percent decrease, such as tax, interest, mark-up, and discounts.
For example, the price tag on a jacket says \$24. The customer must also pay a sales tax equal to 7.5% of the price. What is the total cost of the jacket, including tax?
\(24 \boldcdot 1.075 = 25.80\)
The customer will pay 107.5% of the price listed on the tag, which is \$25.80.
We can also find the percentage. For example, a backpack originally cost \$22.50, but is on sale for \$18.99. The discount is what percentage of the original price?
\(\begin{align} 22.50x &= 18.99 \\ x &= 18.99 \div 22.50 \\ x &= 0.844 \end{align}\)
The sale price is 84.4% of the original price. The discount is $100 - 84.4$, or 15.6% of the original price.
Here is a task to try with your student:
A restaurant bill is \$18.75. If you paid \$22, what percentage tip did you leave for the server?
Solution:
$17.\overline{3}\%$. Possible strategy: You paid $117.\overline{3}\%$ of the bill, because $22 \div 18.75 = 1.17\overline{3}$. You left a $17.\overline{3}\%$ tip, because $117.\overline{3} - 100 = 17.\overline{3}$.