2.1: Number Talk: Multiplying by a Unit Fraction
Find each product mentally.
$\frac14 \boldcdot 32$
$(7.2) \boldcdot \frac19$
Let’s describe features of scaled copies.
Find each product mentally.
$\frac14 \boldcdot 32$
$(7.2) \boldcdot \frac19$
One road sign for railroad crossings is a circle with a large X in the middle and two R’s—with one on each side. Here is a picture with some points labeled and two copies of the picture. Drag and turn the moveable angle tool to compare the angles in the copies with the angles in the original.
| row 1 | original | Copy 1 | Copy 2 |
|---|---|---|---|
| row 2 | point $L$ | ||
| row 3 | segment $LM$ | ||
| row 4 | segment $ED$ | ||
| row 5 | point $X$ | ||
| row 6 | angle $KLM$ | ||
| row 7 | angle $XYZ$ |
Here is Triangle O, followed by a number of other triangles.
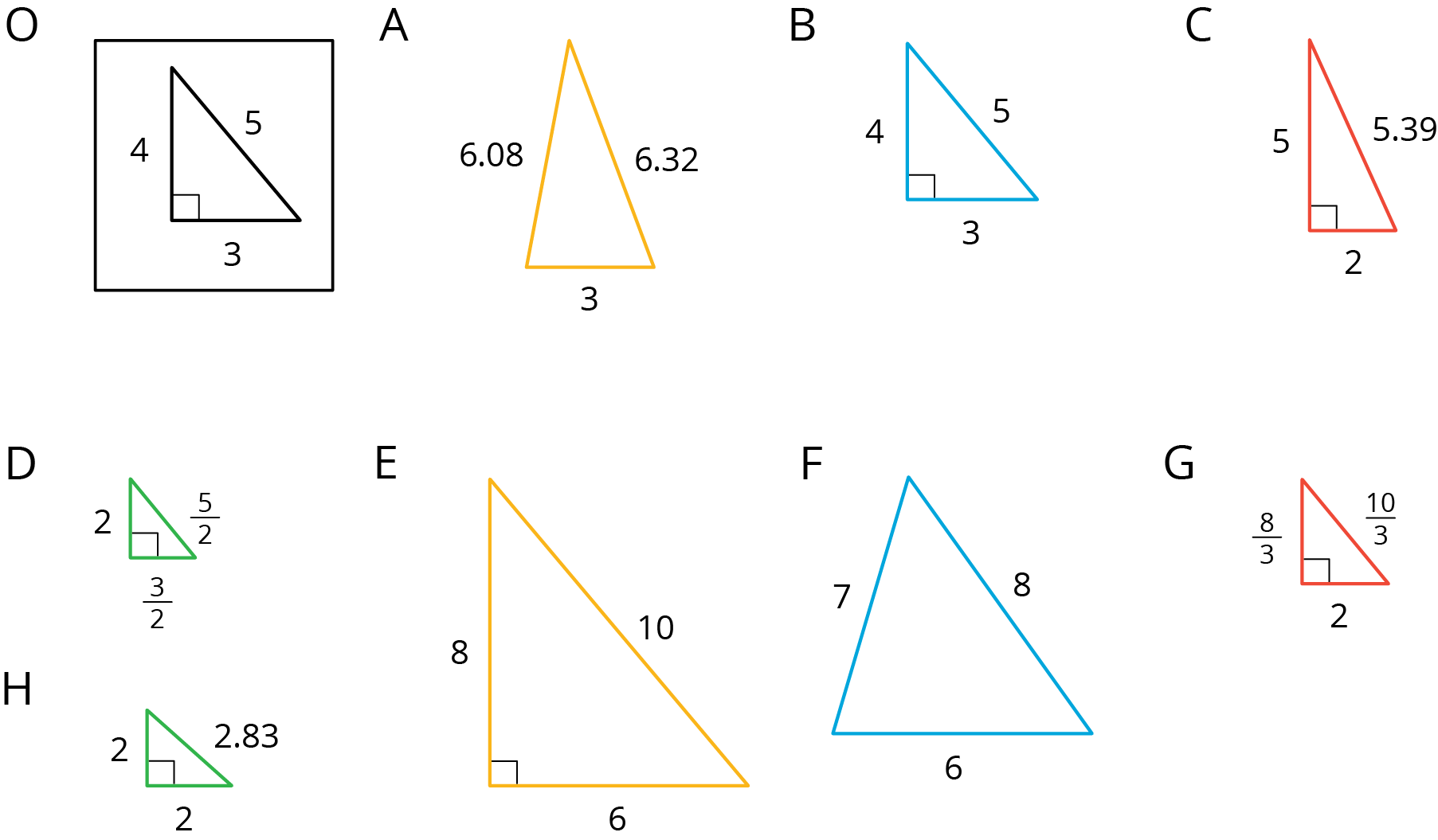
Your teacher will assign you two of the triangles to look at.
| Triangle O | 3 | 4 | 5 | |
|---|---|---|---|---|
| row 1 | ||||
| row 2 | ||||
| row 3 | ||||
| row 4 |
A figure and its scaled copy have corresponding parts, or parts that are in the same position in relation to the rest of each figure. These parts could be points, segments, or angles. For example, Polygon 2 is a scaled copy of Polygon 1.
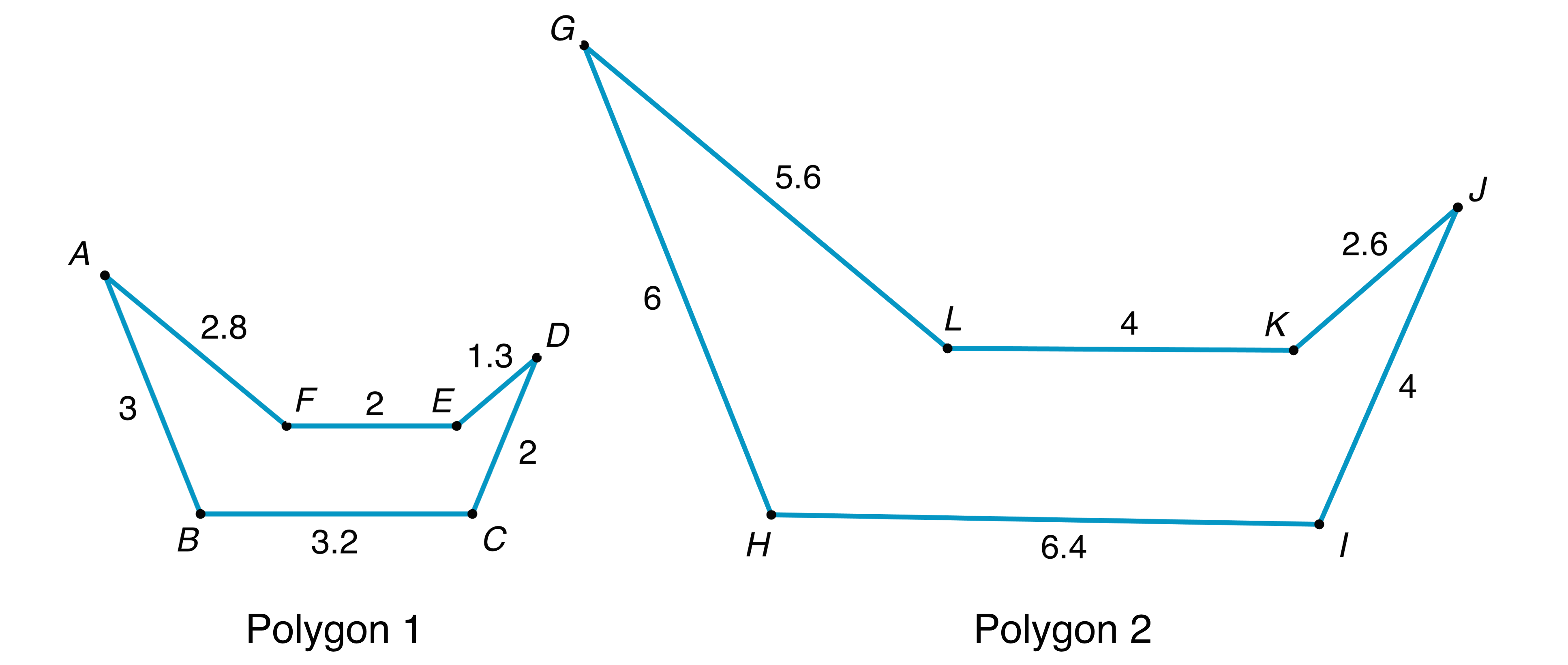
Each point in Polygon 1 has a corresponding point in Polygon 2.
For example, point $B$ corresponds to point $H$ and point $C$ corresponds to point $I$.
Each segment in Polygon 1 has a corresponding segment in Polygon 2.
For example, segment $AF$ corresponds to segment $GL$.
Each angle in Polygon 1 also has a corresponding angle in Polygon 2.
For example, angle $DEF$ corresponds to angle $JKL$.
The scale factor between Polygon 1 and Polygon 2 is 2, because all of the lengths in Polygon 2 are 2 times the corresponding lengths in Polygon 1. The angle measures in Polygon 2 are the same as the corresponding angle measures in Polygon 1: for example, the measure of angle $JKL$ is the same as the measure of angle $DEF$.
The scale factor is the factor by which every length in an original figure is increased or decreased when you make a scaled copy. For example, if you draw a copy of a figure in which every length is magnified by 2, then you have a scaled copy with a scale factor of 2.
If a part of the original figure matches up with a part of the copy, we call them corresponding parts. The part could be an angle, point, or side, and you can have corresponding angles, corresponding points, or corresponding sides.
If you have a distance between two points in the original figure, then the distance between the corresponding points in the copy is called the corresponding distance.