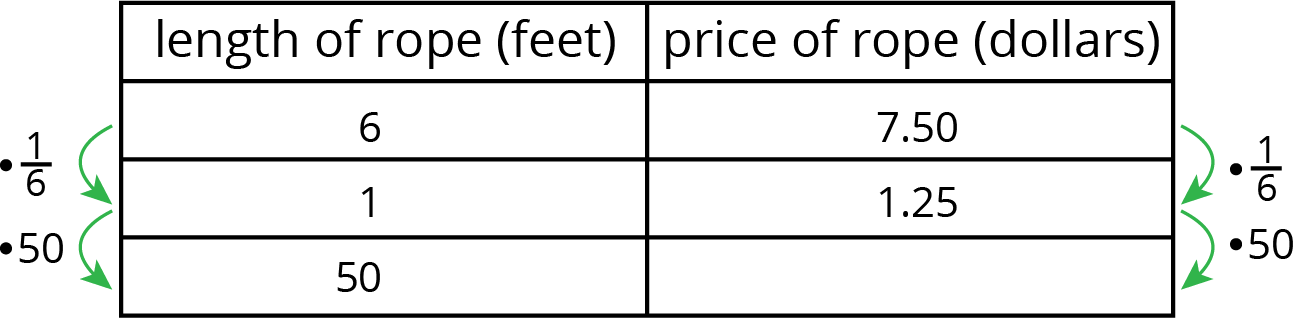
If we identify two quantities in a problem and one is proportional to the other, then we can calculate the constant of proportionality and use it to answer other questions about the situation. For example, Andre runs at a constant speed, 5 meters every 2 seconds. How long does it take him to run 91 meters at this rate?
In this problem there are two quantities, time (in seconds) and distance (in meters). Since Andre is running at a constant speed, time is proportional to distance. We can make a table with distance and time as column headers and fill in the given information.
| |
distance (meters) |
time (seconds) |
| row 1 |
5 |
2 |
| row 2 |
91 |
|
To find the value in the right column, we multiply the value in the left column by $\frac25$ because $\frac25 \boldcdot 5 = 2$. This means that it takes Andre $\frac25$ seconds to run one meter.
At this rate, it would take Andre $\frac25 \boldcdot 91 = \frac{182}{5}$, or 36.4 seconds to walk 91 meters. In general, if $t$ is the time it takes to walk $d$ meters at that pace, then $t = \frac25 d$.