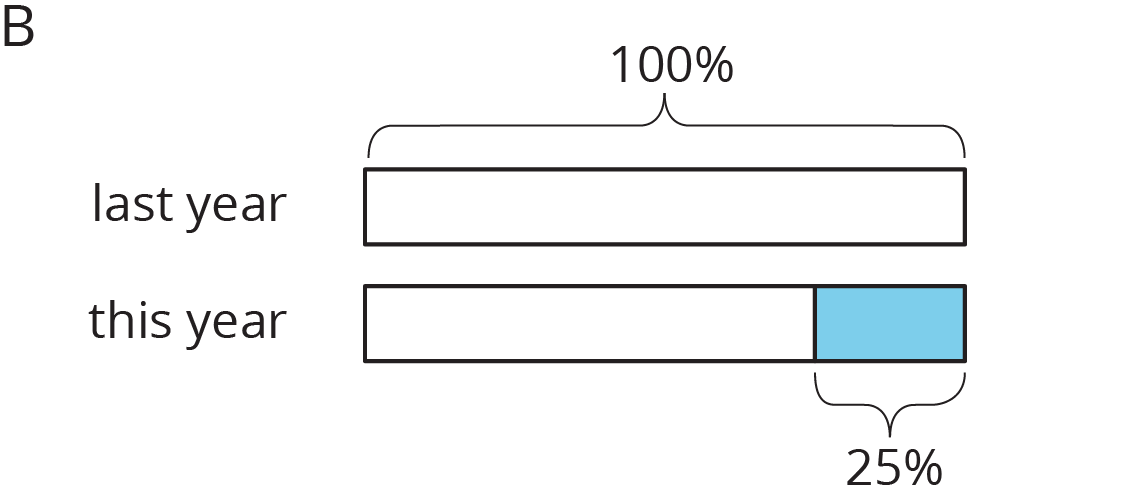
Imagine that it takes Andre $\frac34$ more than the time it takes Jada to get to school. Then we know that Andre’s time is $1\frac34$ or 1.75 times Jada’s time. We can also describe this in terms of percentages:
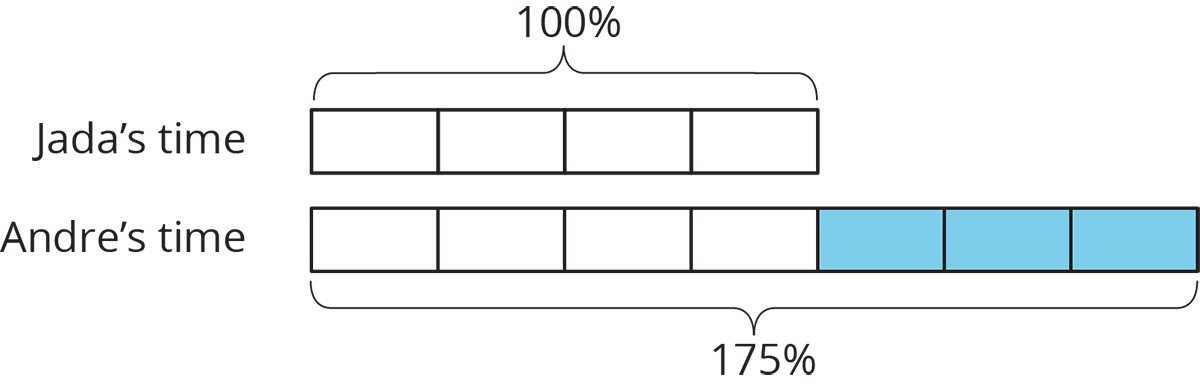
We say that Andre’s time is 75% more than Jada’s time. We can also see that Andre’s time is 175% of Jada’s time. In general, the terms percent increase and percent decrease describe an increase or decrease in a quantity as a percentage of the starting amount.
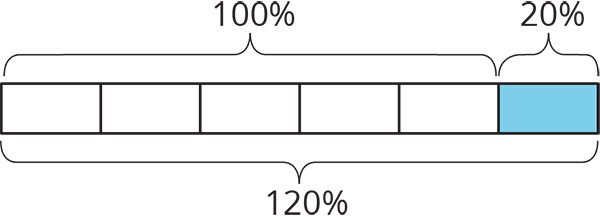
For example, if there were 500 grams of cereal in the original package, then “20% more” means that 20% of 500 grams has been added to the initial amount, $500+(0.2)\boldcdot 500=600$, so there are 600 grams of cereal in the new package.
We can see that the new amount is 120% of the initial amount because
$$500+(0.2)\boldcdot 500 = (1 + 0.2)500$$