7.1: Notice and Wonder: Double Number Line
What do you notice? What do you wonder?
Let’s solve more problems about percent increase and percent decrease.

What do you notice? What do you wonder?
For each problem, complete the double number line diagram to show the percentages that correspond to the original amount and to the new amount.
The gas tank in dad’s car holds 12 gallons. The gas tank in mom’s truck holds 50% more than that. How much gas does the truck’s tank hold?

At a movie theater, the size of popcorn bags decreased 20%. If the old bags held 15 cups of popcorn, how much do the new bags hold?

A school had 1,200 students last year and only 1,080 students this year. What was the percentage decrease in the number of students?

One week gas was \$1.25 per gallon. The next week gas was \$1.50 per gallon. By what percentage did the price increase?

After a 25% discount, the price of a T-shirt was \$12. What was the price before the discount?

Compared to last year, the population of Boom Town has increased 25%.The population is now 6,600. What was the population last year?

Two students are working on the same problem:
A juice box has 20% more juice in its new packaging. The original packaging held 12 fluid ounces. How much juice does the new packaging hold?


Do you agree with either of them? Explain or show your reasoning.
Green sea turtles live most of their lives in the ocean, but come ashore to lay their eggs. Some beaches where turtles often come ashore have been made into protected sanctuaries so the eggs will not be disturbed.

We can use a double number line diagram to show information about percent increase and percent decrease:
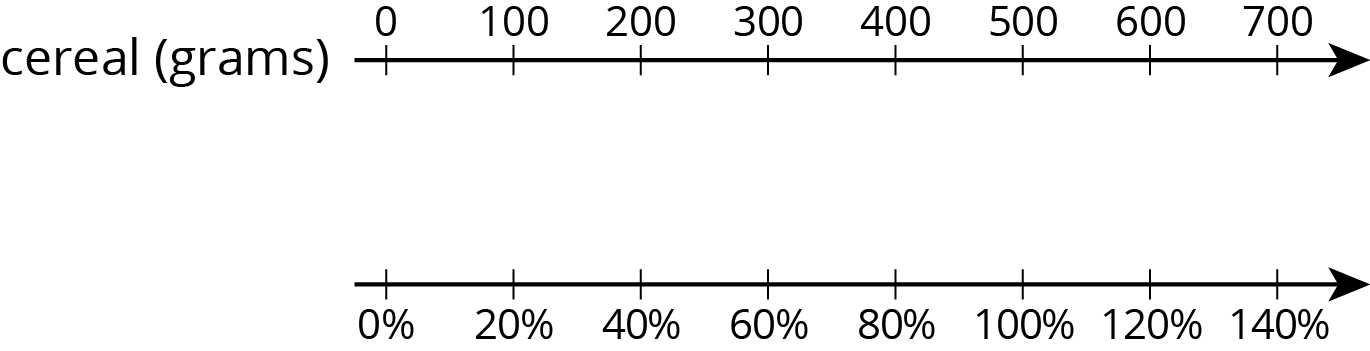
The initial amount of cereal is 500 grams, which is lined up with 100% in the diagram. We can find a 20% increase to 500 by adding 20% of 500:
\(\begin{align}500+(0.2)\boldcdot 500 &= (1.20)\boldcdot 500\\&=600\end{align}\)
In the diagram, we can see that 600 corresponds to 120%.
If the initial amount of 500 grams is decreased by 40%, we can find how much cereal there is by subtracting 40% of the 500 grams:
\(\begin{align}500−(0.4)\boldcdot 500 &= (0.6)\boldcdot 500\\&=300\end{align}\)
So a 40% decrease is the same as 60% of the initial amount. In the diagram, we can see that 300 is lined up with 60%.
To solve percentage problems, we need to be clear about what corresponds to 100%. For example, suppose there are 20 students in a class, and we know this is an increase of 25% from last year. In this case, the number of students in the class last year corresponds to 100%. So the initial amount (100%) is unknown and the final amount (125%) is 20 students.
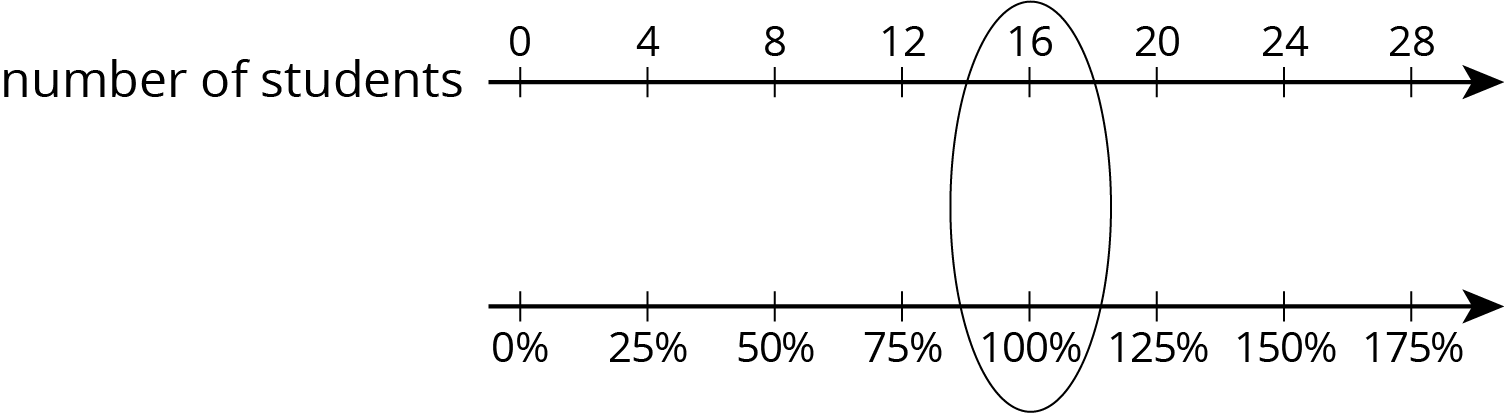
Looking at the double number line, if 20 students is a 25% increase from the previous year, then there were 16 students in the class last year.