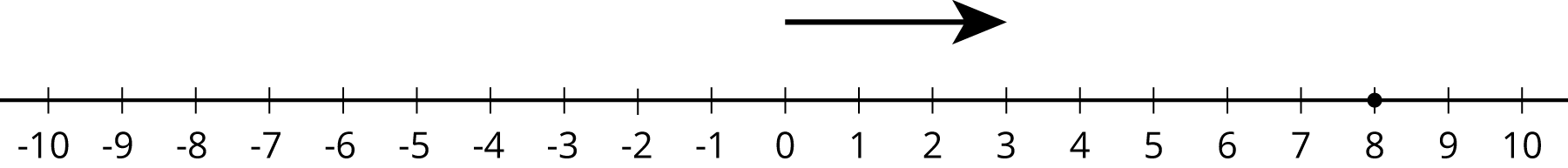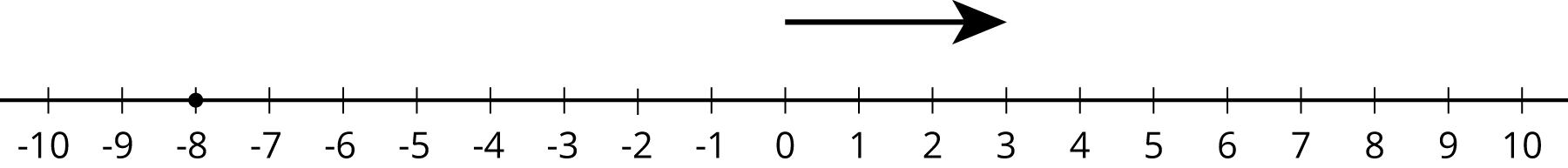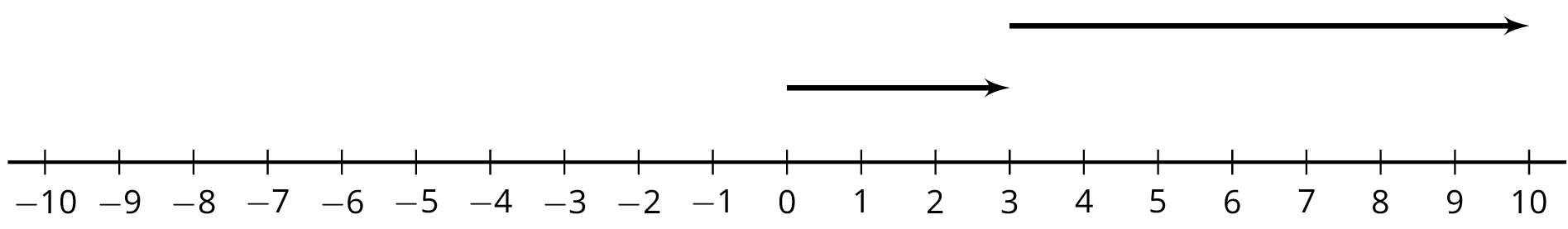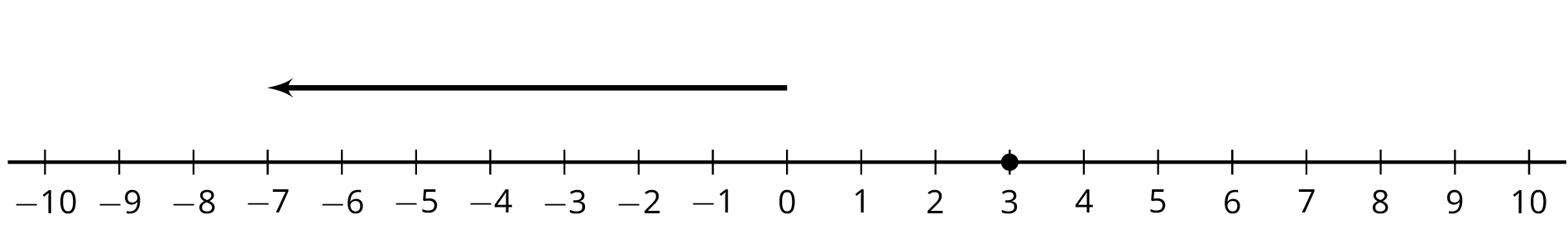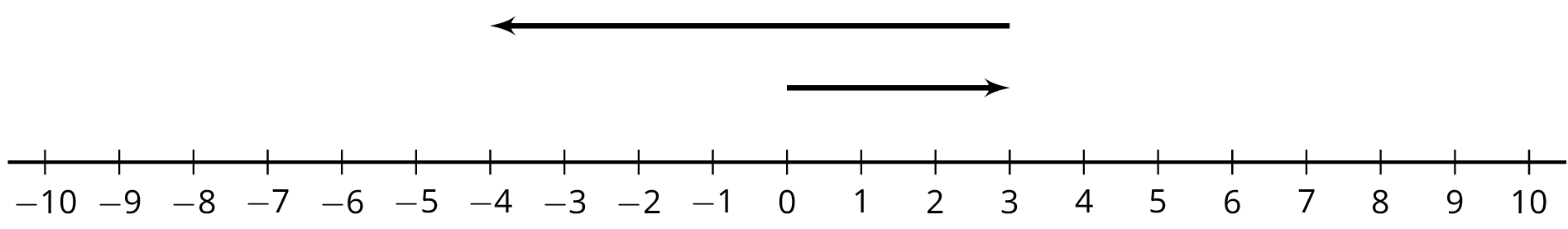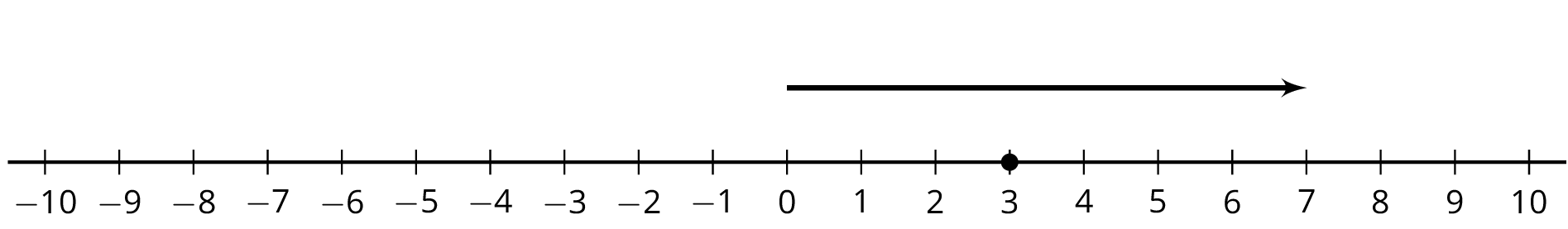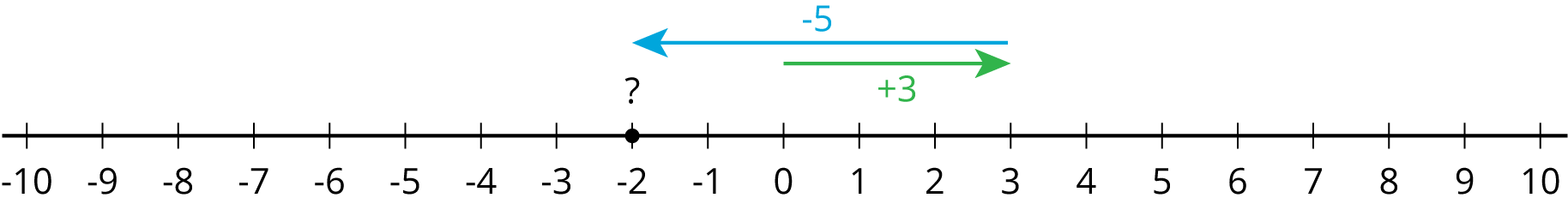5.1: Equivalent Equations
For the equations in the second and third columns, write two more equations using the same numbers that express the same relationship in a different way. If you get stuck, consider looking at the examples in the first column.
$2+ 3= 5$
$3 + 2 = 5$
$5 - 3 = 2$
$5 - 2 = 3$
$9+ (\text- 1)= 8$
$\text- 11+ x= 7$