19.1: Number Talk: Parentheses
Find the value of each expression mentally.
$2 + 3 \boldcdot 4$
$(2+3)(4)$
$2 - 3 \boldcdot 4$
Let's use the distributive property to write expressions in different ways.
Find the value of each expression mentally.
$2 + 3 \boldcdot 4$
$(2+3)(4)$
$2 - 3 \boldcdot 4$
In each row, write the equivalent expression. If you get stuck, use a diagram to organize your work. The first row is provided as an example. Diagrams are provided for the first three rows.
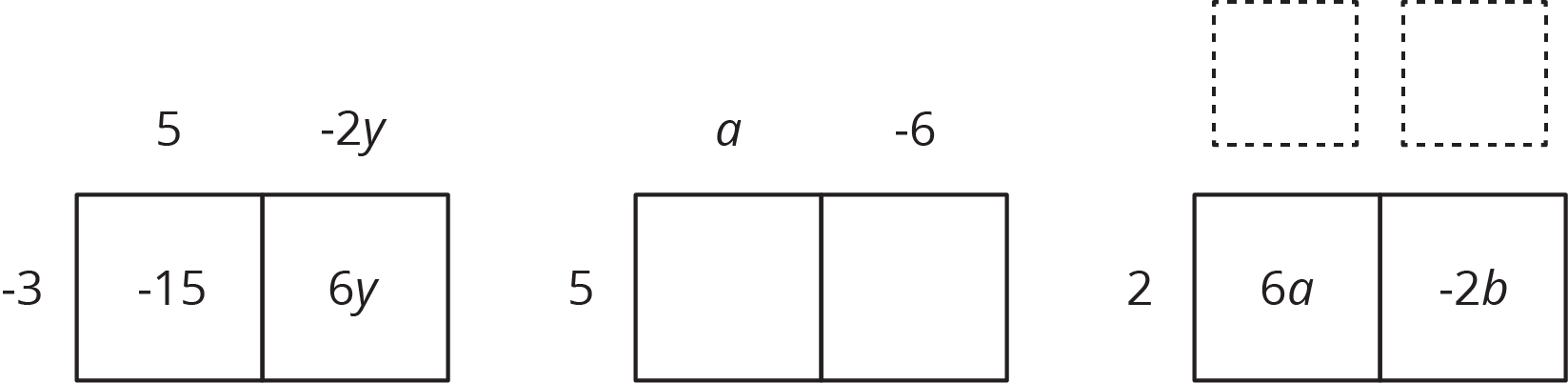
| factored | expanded | |
|---|---|---|
| row 1 | $\text- 3(5 - 2y)$ | $\text- 15 + 6y$ |
| row 2 | $5(a-6)$ | |
| row 3 | $6a-2b$ | |
| row 4 | $\text- 4(2w-5z)$ | |
| row 5 | $\text- (2x-3y)$ | |
| row 6 | $20x-10y+15z$ | |
| row 7 | $k(4-17)$ | |
| row 8 | $10a-13a$ | |
| row 9 | $\text- 2x(3y-z)$ | |
| row 10 | $ab-bc-3bd$ | |
| row 11 | $\text- x(3y-z+4w)$ |
Expand to create an equivalent expression that uses the fewest number of terms: $\left(\left(\left(\left(x\strut+1\right)\frac12\right)+1\right)\frac12\right)+1$. If we wrote a new expression following the same pattern so that there were 20 sets of parentheses, how could it be expanded into an equivalent expression that uses the fewest number of terms?
We can use properties of operations in different ways to rewrite expressions and create equivalent expressions. We have already seen that we can use the distributive property to expand an expression, for example $3(x+5) = 3x+15$. We can also use the distributive property in the other direction and factor an expression, for example $8x+12 = 4(2x+3)$.
We can organize the work of using distributive property to rewrite the expression $12x-8$. In this case we know the product and need to find the factors.
The terms of the product go inside:
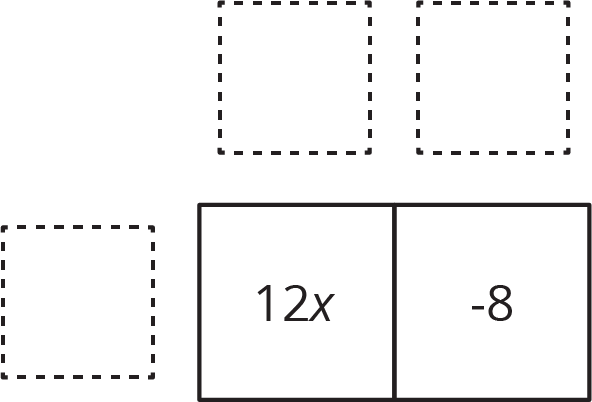
We look at the expressions and think about a factor they have in common. $12x$ and $\text- 8$ each have a factor of 4. We place the common factor on one side of the large rectangle:
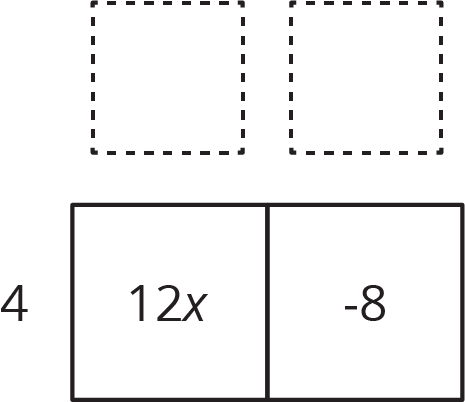
Now we think: "4 times what is 12$x$?" "4 times what is -8?" and write the other factors on the other side of the rectangle:

So, $12x-8$ is equivalent to $4(3x-2)$.