A triangle has six measures: three side lengths and three angle measures.
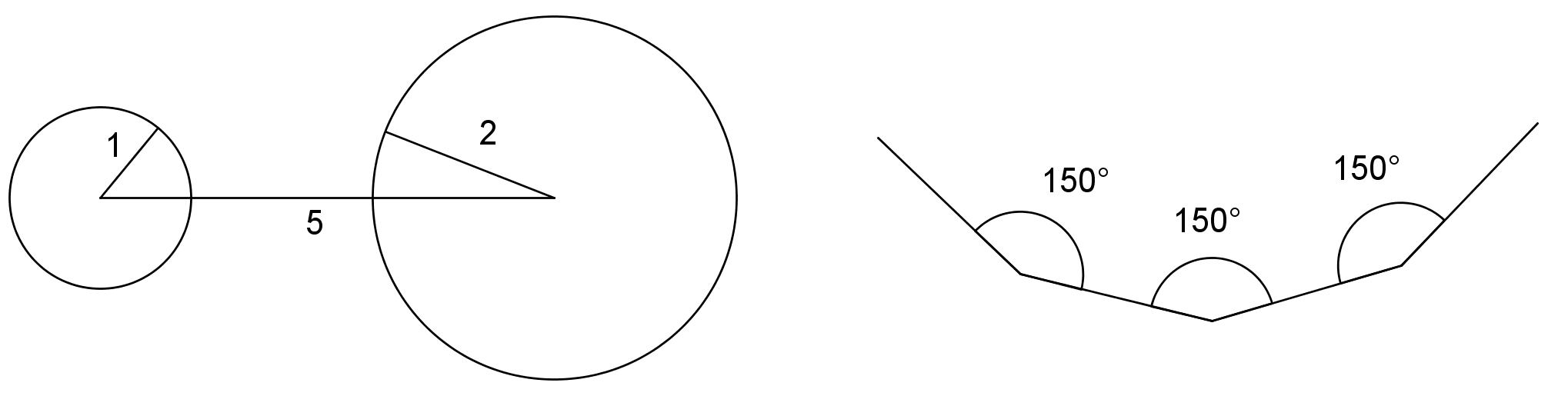
If we are given three measures, then sometimes, there is no triangle that can be made. For example, there is no triangle with side lengths 1, 2, 5, and there is no triangle with all three angles measuring $150^\circ$.
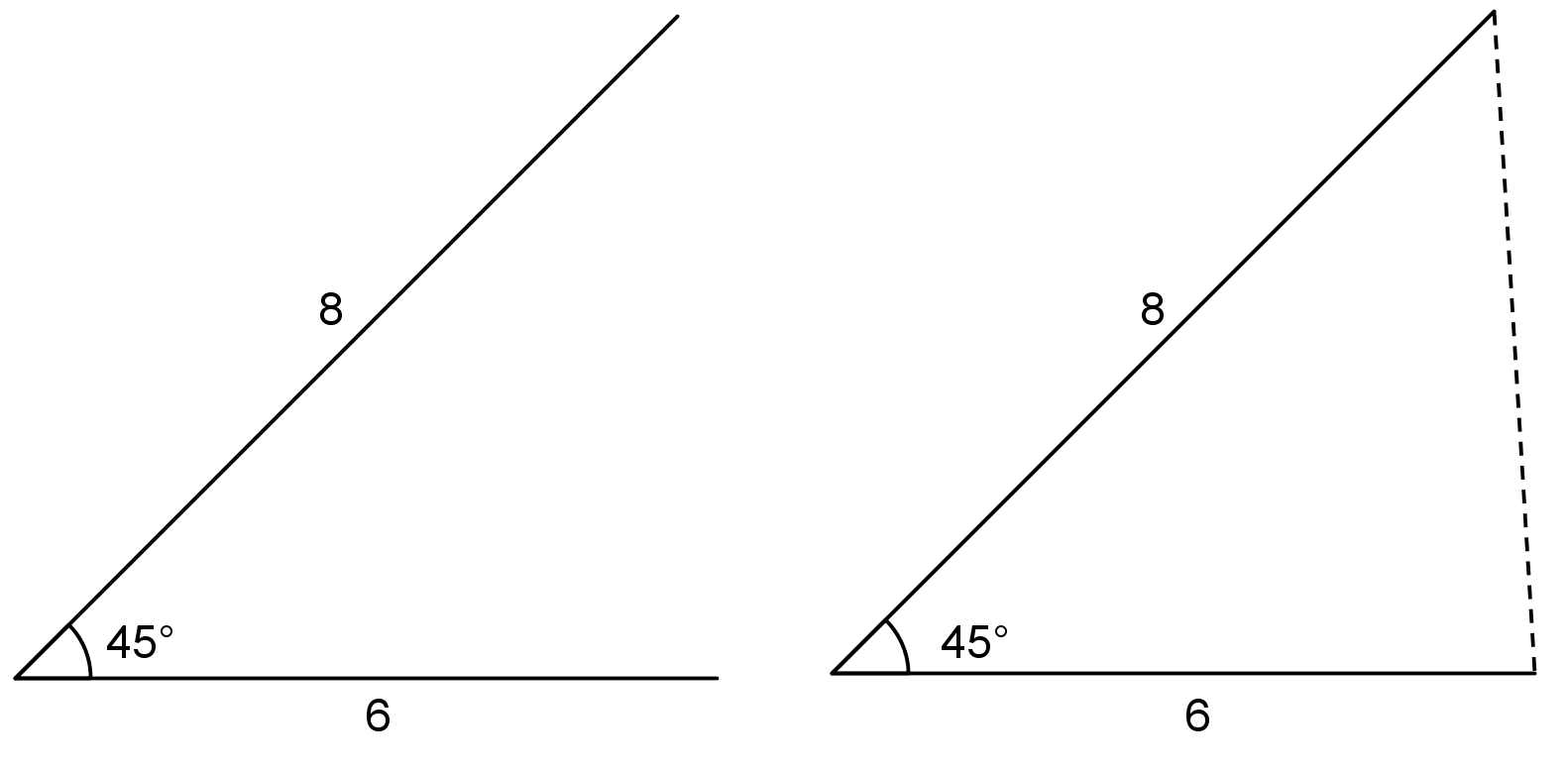
Sometimes, only one triangle can be made. By this we mean that any triangle we make will be the same, having the same six measures. For example, if a triangle can be made with three given side lengths, then the corresponding angles will have the same measures. Another example is shown here: an angle measuring $45^\circ$ between two side lengths of 6 and 8 units. With this information, one unique triangle can be made.
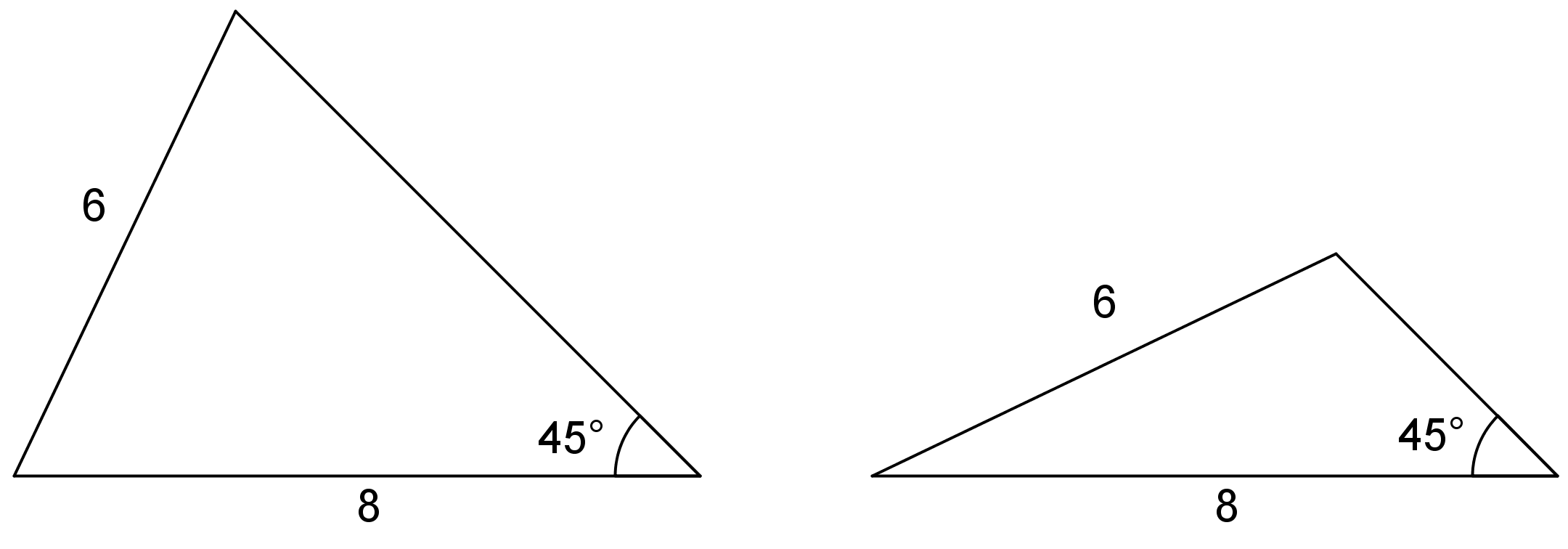
Sometimes, two or more different triangles can be made with three given measures. For example, here are two different triangles that can be made with an angle measuring $45^\circ$ and side lengths 6 and 8. Notice the angle is not between the given sides.
Three pieces of information about a triangle’s side lengths and angle measures may determine no triangles, one unique triangle, or more than one triangle. It depends on the information.


