Lesson 4: Solving for Unknown Angles

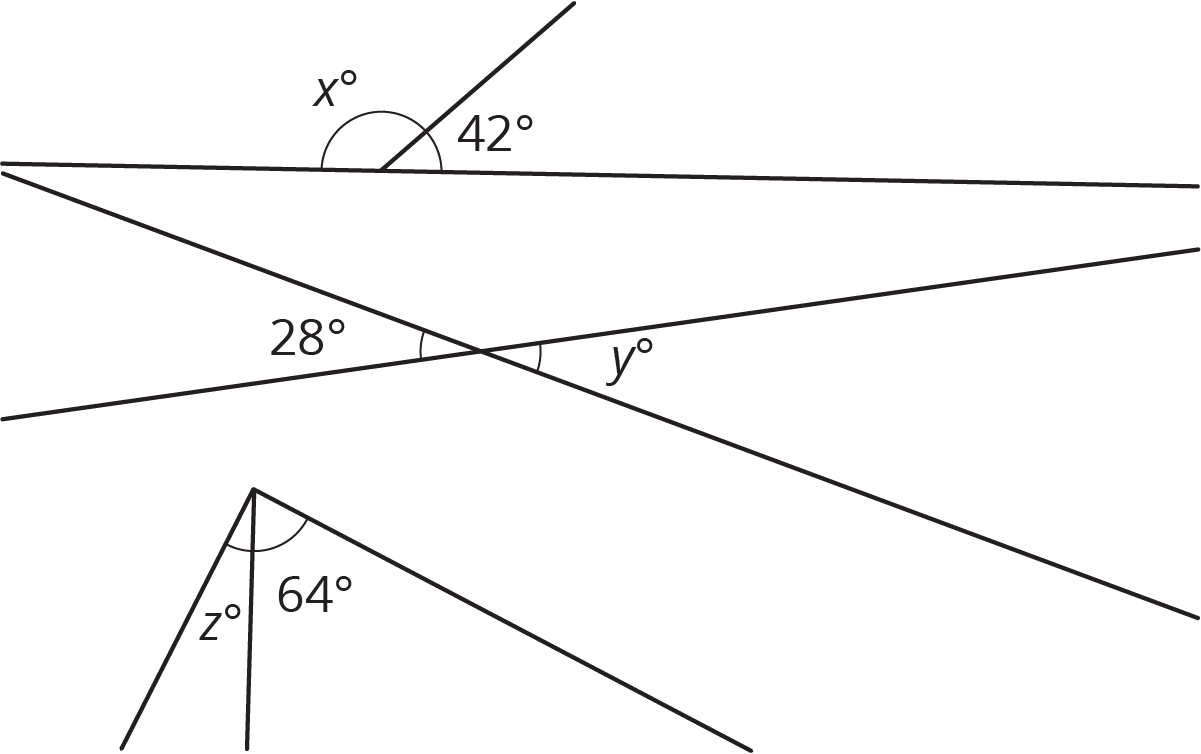
Let’s figure out some missing angles.

Here are some line segments.

Decide if each of these equations is true or false. Be prepared to explain your reasoning.

$CD+BC=BD$

$AB+BD=CD+AD$

$AC-AB=AB$

$BD-CD=AC-AB$

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the problem card:

Silently read your card and think about what information you need to answer the question.
Ask your partner for the specific information that you need.
Explain to your partner how you are using the information to solve the problem.
Solve the problem and explain your reasoning to your partner.

If your teacher gives you the data card:

Silently read the information on your card.
Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
Before telling your partner the information, ask “Why do you need that information?”
After your partner solves the problem, ask them to explain their reasoning and listen to their explanation.

Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.

Match each figure to an equation that represents what is seen in the figure. For each match, explain how you know they are a match.

What is the angle between the hour and minute hands of a clock at 3:00?
You might think that the angle between the hour and minute hands at 2:20 is 60 degrees, but it is not! The hour hand has moved beyond the 2. Calculate the angle between the clock hands at 2:20.
Find a time where the hour and minute hand are 40 degrees apart. (Assume that the time has a whole number of minutes.) Is there just one answer?

Summary

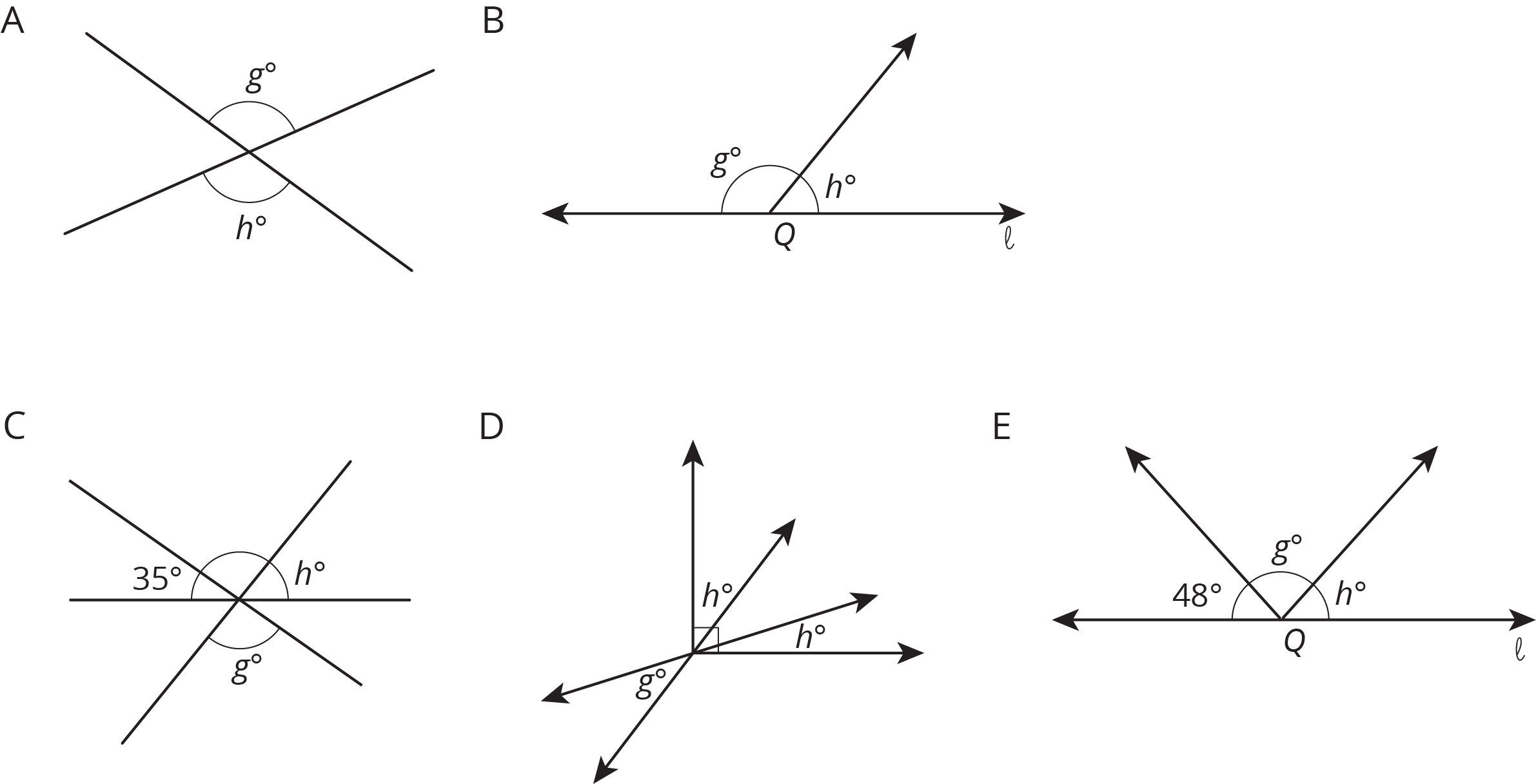
We can write equations that represent relationships between angles.