Draw a right angle. How do you know it’s a right angle? What is its measure in degrees?
Unit 7: Practice Problem Sets
Lesson 1
Problem 1
Here are questions about two types of angles.
Draw a straight angle. How do you know it’s a straight angle? What is its measure in degrees?
Problem 2
An equilateral triangle’s angles each have a measure of 60 degrees.
-
Can you put copies of an equilateral triangle together to form a straight angle? Explain or show your reasoning.
-
Can you put copies of an equilateral triangle together to form a right angle? Explain or show your reasoning.
Problem 3
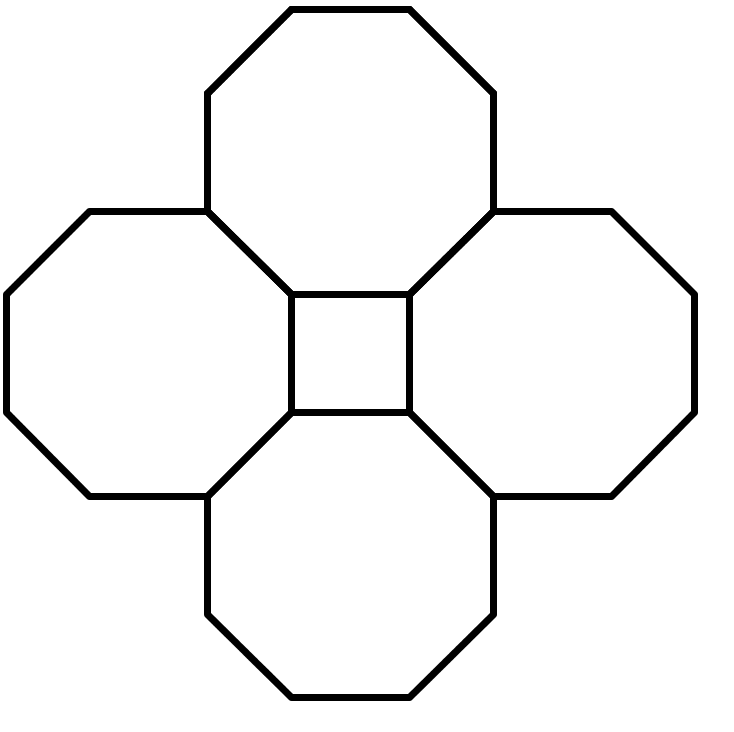
Here is a square and some regular octagons.
In this pattern, all of the angles inside the octagons have the same measure. The shape in the center is a square. Find the measure of one of the angles inside one of the octagons.
Problem 4 (from Unit 6, Lesson 17)
The height of the water in a tank decreases by 3.5 cm each day. When the tank is full, the water is 10 m deep. The water tank needs to be refilled when the water height drops below 4 m.
- Write a question that could be answered by solving the equation $10-0.035d=4$.
- Is 100 a solution of $10-0.035d>4$? Write a question that solving this problem could answer.
Problem 5 (from Unit 6, Lesson 18)
Use the distributive property to write an expression that is equivalent to each given expression.
- $\text-3(2x-4)$
- $0.1(\text-90+50a)$
- $\text-7(\text-x-9)$
- $\frac45(10y+\text-x+\text-15)$
Problem 6 (from Unit 2, Lesson 3)
Lin’s puppy is gaining weight at a rate of 0.125 pounds per day. Describe the weight gain in days per pound.
Lesson 2
Problem 1
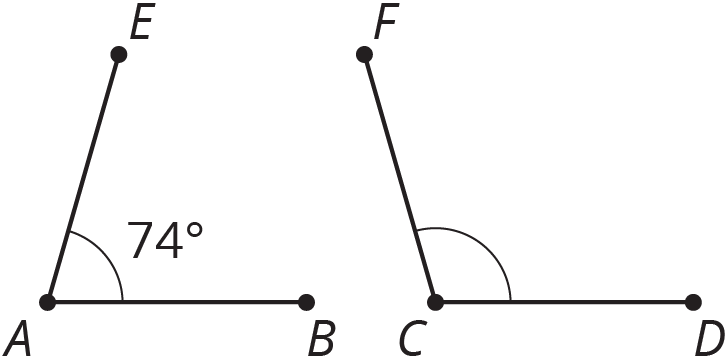
Angles $A$ and $C$ are supplementary. Find the measure of angle $C$.
Problem 2
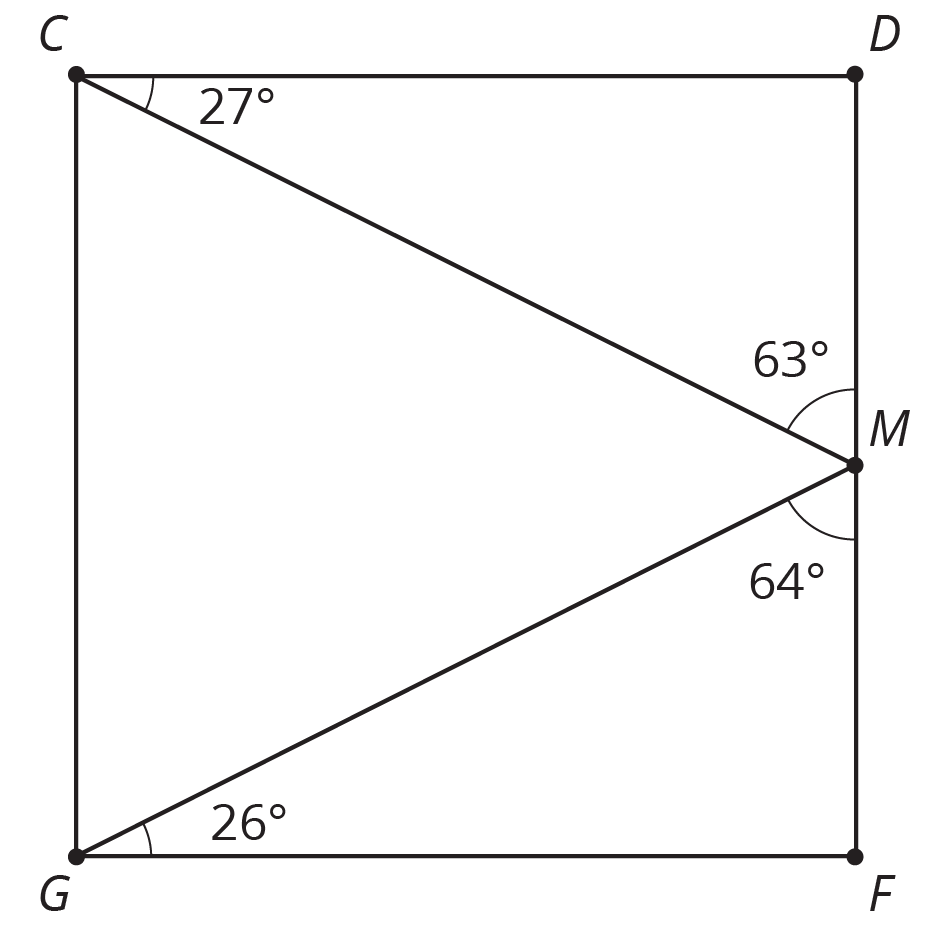
-
List two pairs of angles in square $CDFG$ that are complementary.
- Name three angles that sum to $180^\circ$.
Problem 3 (from Unit 6, Lesson 22)
Complete the equation with a number that makes the expression on the right side of the equal sign equivalent to the expression on the left side.
$$5x-2.5 +6x-3 = \underline{\ \ \ \ }(2x-1)$$
Problem 4 (from Unit 2, Lesson 4)
Match each table with the equation that represents the same proportional relationship.
-
$x$ $y$ row 1 2 8 row 2 3 12 row 3 4 16 row 4 5 20 -
$x$ $y$ row 1 3 4.5 row 2 6 9 row 3 7 10.5 row 4 10 15 -
$x$ $y$ row 1 2 $\frac52$ row 2 4 5 row 3 6 $\frac{15}{2}$ row 4 12 15
- $y=1.5x$
- $y=1.25x$
- $y=4x$
Lesson 3
Problem 1
Two lines intersect. Find the value of $b$ and $c$. 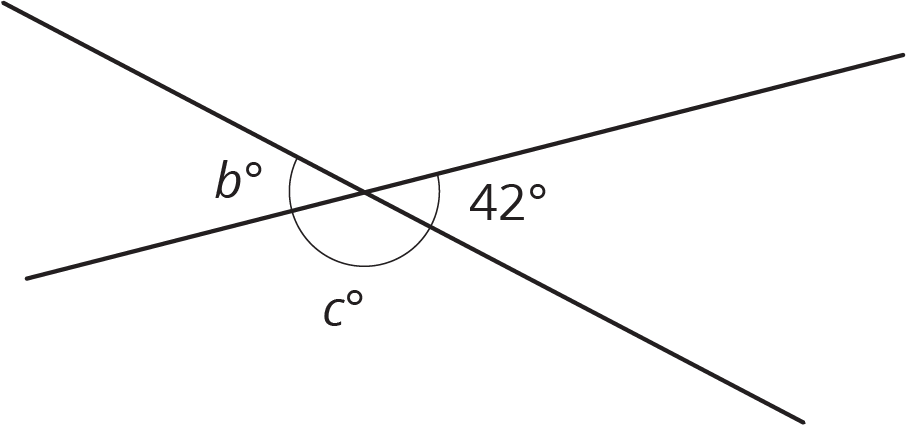
Problem 2
In this figure, angles $R$ and $S$ are complementary. Find the measure of angle $S$. 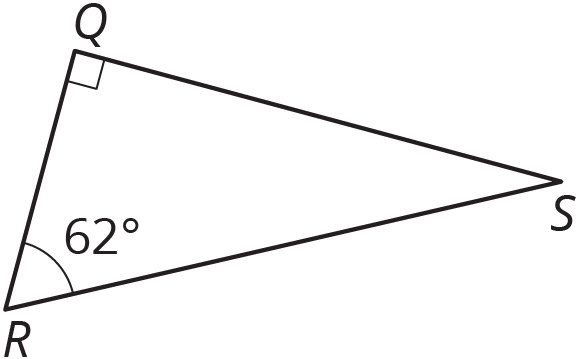
Problem 3
If two angles are both vertical and supplementary, can we determine the angles? Is it possible to be both vertical and complementary? If so, can you determine the angles? Explain how you know.
Problem 4 (from Unit 6, Lesson 22)
Match each expression in the first list with an equivalent expression from the second list.
- $5(x+1) - 2x + 11$
- $2x + 2 + x + 5$
- $\frac {\text{-}3}{8}x - 9 + \frac58x + 1$
- $2.06x - 5.53 + 4.98 - 9.02$
- $99x + 44$
- $\frac14x - 8$
- $\frac12(6x+14)$
- $11(9x+4)$
- $3x+16$
- $2.06x +(\text-5.53) + 4.98 + (\text-9.02)$
Problem 5 (from Unit 6, Lesson 19)
Factor each expression.
- $15a-13a$
- $\text-6x-18y$
- $36abc+54ad$
Problem 6 (from Unit 6, Lesson 17)
The directors of a dance show expect many students to participate but don’t yet know how many students will come. The directors need 7 students to work on the technical crew. The rest of the students work on dance routines in groups of 9. For the show to work, they need at least 6 full groups working on dance routines.
- Write and solve an inequality to represent this situation, and graph the solution on a number line.
- Write a sentence to the directors about the number of students they need.
Problem 7 (from Unit 2, Lesson 5)
A small dog gets fed $\frac{3}{4}$ cup of dog food twice a day. Using $d$ for the number of days and $f$ for the amount of food in cups, write an equation relating the variables. Use the equation to find how many days a large bag of dog food will last if it contains 210 cups of food.
Lesson 4
Problem 1
$M$ is a point on line segment $KL$. $NM$ is a line segment. Select all the equations that represent the relationship between the measures of the angles in the figure.
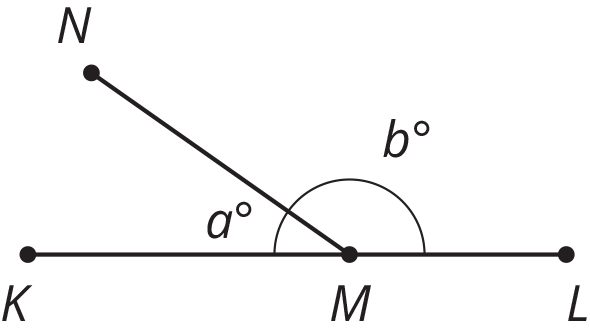
- $a=b$
- $a+b=90$
- $b=90-a$
- $a+b=180$
- $180-a=b$
- $180=b-a$
Problem 2
Which equation represents the relationship between the angles in the figure?
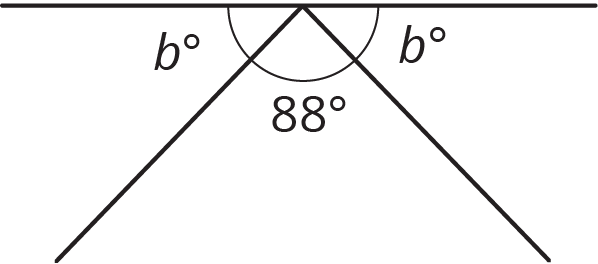
- $88+b=90$
- $88+b=180$
- $2b+88=90$
- $2b+88=180$
Problem 3
Segments $AB$, $EF$, and $CD$ intersect at point $C$, and angle $ACD$ is a right angle. Find the value of $g$.
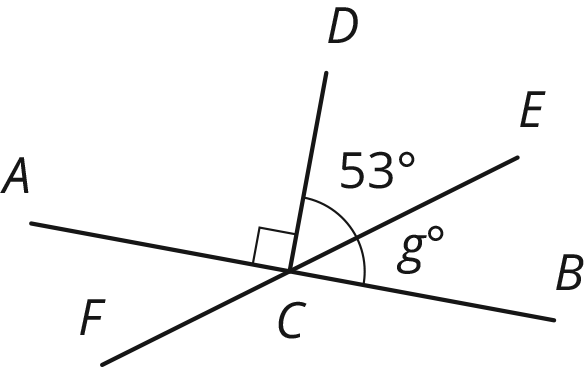
Problem 4 (from Unit 6, Lesson 12)
Select all the expressions that are the result of decreasing $x$ by 80%.
- $\frac{20}{100}x$
- $x - \frac{80}{100}x$
- $\frac{100-20}{100}x$
- $0.80x$
- $(1-0.8)x$
Problem 5 (from Unit 6, Lesson 8)
Andre is solving the equation $4(x+\frac32)=7$. He says, “I can subtract $\frac32$ from each side to get $4x=\frac{11}{2}$ and then divide by 4 to get $x=\frac{11}{8}$.” Kiran says, “I think you made a mistake.”
- How can Kiran know for sure that Andre’s solution is incorrect?
- Describe Andre’s error and explain how to correct his work.
Problem 6 (from Unit 6, Lesson 7)
Solve each equation.
- $\frac17x+\frac34=\frac98$
- $\frac23+\frac15x=\frac56$
- $\frac32=\frac43x+\frac23$
- $0.3x+7.9=9.1$
- $11.03=8.78+0.02x$
Problem 7 (from Unit 2, Lesson 5)
A train travels at a constant speed for a long distance. Write the two constants of proportionality for the relationship between distance traveled and elapsed time. Explain what each of them means.
| Row 1 | time elapsed (hr) | distance (mi) |
|---|---|---|
| Row 2 | 1.2 | 54 |
| Row 3 | 3 | 135 |
| Row 4 | 4 | 180 |
Lesson 5
Problem 1
Segments $AB$, $DC$, and $EC$ intersect at point $C$. Angle $DCE$ measures $148^\circ$. Find the value of $x$.

Problem 2
Line $\ell$ is perpendicular to line $m$. Find the value of $x$ and $w$.
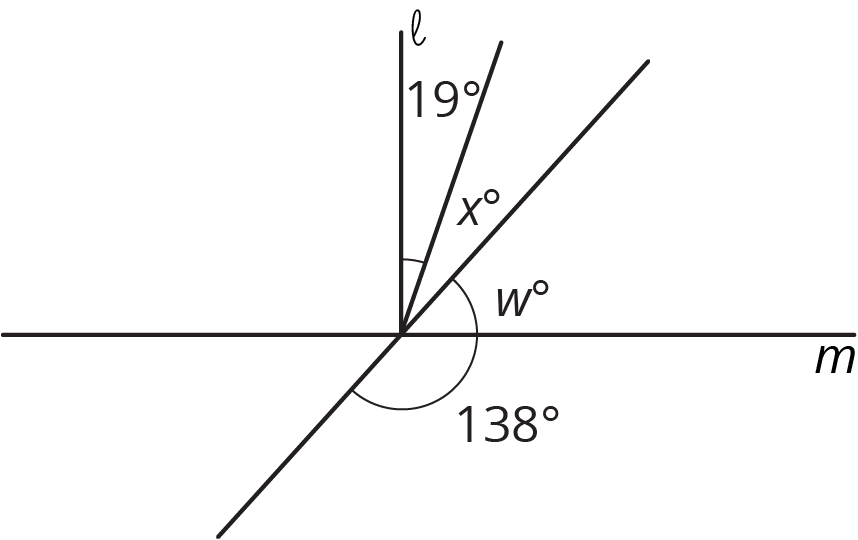
Problem 3
If you knew that two angles were complementary and were given the measure of one of those angles, would you be able to find the measure of the other angle? Explain your reasoning.
Problem 4 (from Unit 6, Lesson 15)
For each inequality, decide whether the solution is represented by $x < 4.5$ or $x > 4.5$.
- $\text-24>\text-6(x-0.5)$
- $\text-8x + 6 > \text-30$
- $\text-2(x + 3.2) < \text-15.4$
Problem 5 (from Unit 4, Lesson 2)
A runner ran $\frac23$ of a 5 kilometer race in 21 minutes. They ran the entire race at a constant speed.
- How long did it take to run the entire race?
- How many minutes did it take to run 1 kilometer?
Problem 6 (from Unit 6, Lesson 12)
Jada, Elena, and Lin walked a total of 37 miles last week. Jada walked 4 more miles than Elena, and Lin walked 2 more miles than Jada. The diagram represents this situation:
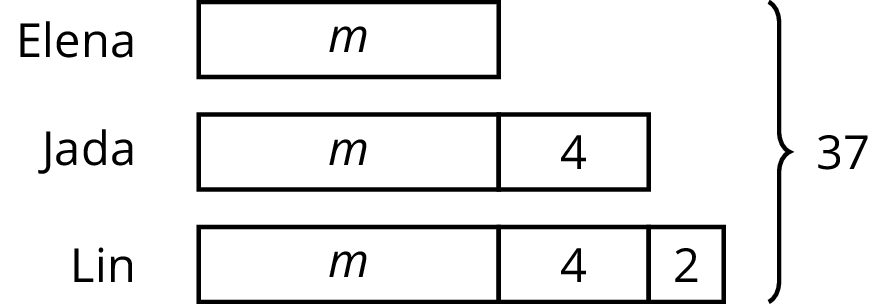
Find the number of miles that they each walked. Explain or show your reasoning.
Problem 7 (from Unit 6, Lesson 19)
Select all the expressions that are equivalent to $\text-36x+54y-90$.
- $\text-9(4x-6y-10)$
- $\text-18(2x-3y+5)$
- $\text-6(6x+9y-15)$
- $18(\text-2x+3y-5)$
- $\text-2(18x-27y+45)$
- $2(\text-18x+54y-90)$
Lesson 6
Problem 1
A rectangle has side lengths of 6 units and 3 units. Could you make a quadrilateral that is not identical using the same four side lengths? If so, describe it.
Problem 2
Come up with an example of three side lengths that can not possibly make a triangle, and explain how you know.
Problem 3 (from Unit 7, Lesson 3)
Find $x$, $y$, and $z$.
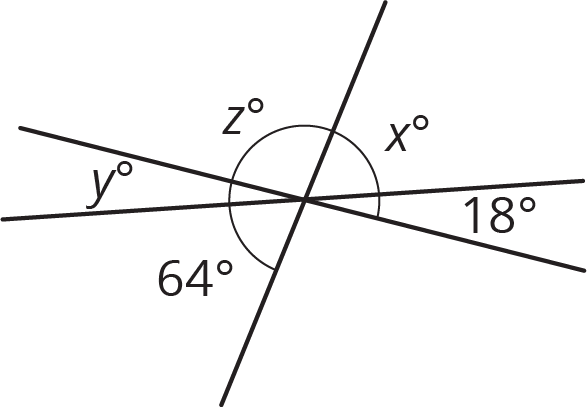
Problem 4 (from Unit 7, Lesson 1)
How many right angles need to be put together to make:
- 360 degrees?
- 180 degrees?
- 270 degrees?
- A straight angle?
Problem 5 (from Unit 6, Lesson 8)
Solve each equation.
$\frac17(x+\frac34)=\frac18$
$\frac92=\frac34(z+\frac23)$
$1.5=0.6(w+0.4)$
$0.08(7.97+v)=0.832$
Problem 6 (from Unit 4, Lesson 3)
- You can buy 4 bottles of water from a vending machine for \$7. At this rate, how many bottles of water can you buy for \$28? If you get stuck, consider creating a table.
- It costs \$20 to buy 5 sandwiches from a vending machine. At this rate, what is the cost for 8 sandwiches? If you get stuck, consider creating a table.
Lesson 7
Problem 1
In the diagram, the length of segment $AB$ is 10 units and the radius of the circle centered at $A$ is 4 units. Use this to create two unique triangles, each with a side of length 10 and a side of length 4. Label the sides that have length 10 and 4. 
Problem 2
Select all the sets of three side lengths that will make a triangle.
- 3, 4, 8
- 7, 6, 12
- 5, 11, 13
- 4, 6, 12
- 4, 6, 10
Problem 3
Problem 4 (from Unit 7, Lesson 2)
Each row contains the degree measures of two complementary angles. Complete the table.
| measure of an angle | measure of its complement | |
|---|---|---|
| row 1 | $80^\circ$ | |
| row 2 | $25^\circ$ | |
| row 3 | $54^\circ$ | |
| row 4 | $x$ |
Problem 5 (from Unit 7, Lesson 1)
Here are two patterns made using identical rhombuses. Without using a protractor, determine the value of $a$ and $b$. Explain or show your reasoning.
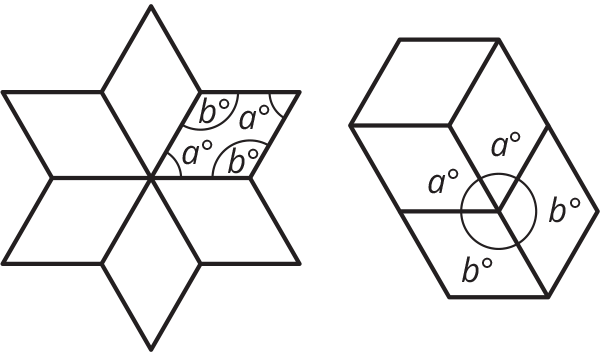
Problem 6 (from Unit 4, Lesson 3)
Mai’s family is traveling in a car at a constant speed of 65 miles per hour.
- At that speed, how long will it take them to travel 200 miles?
- How far do they travel in 25 minutes?
Lesson 8
Problem 1
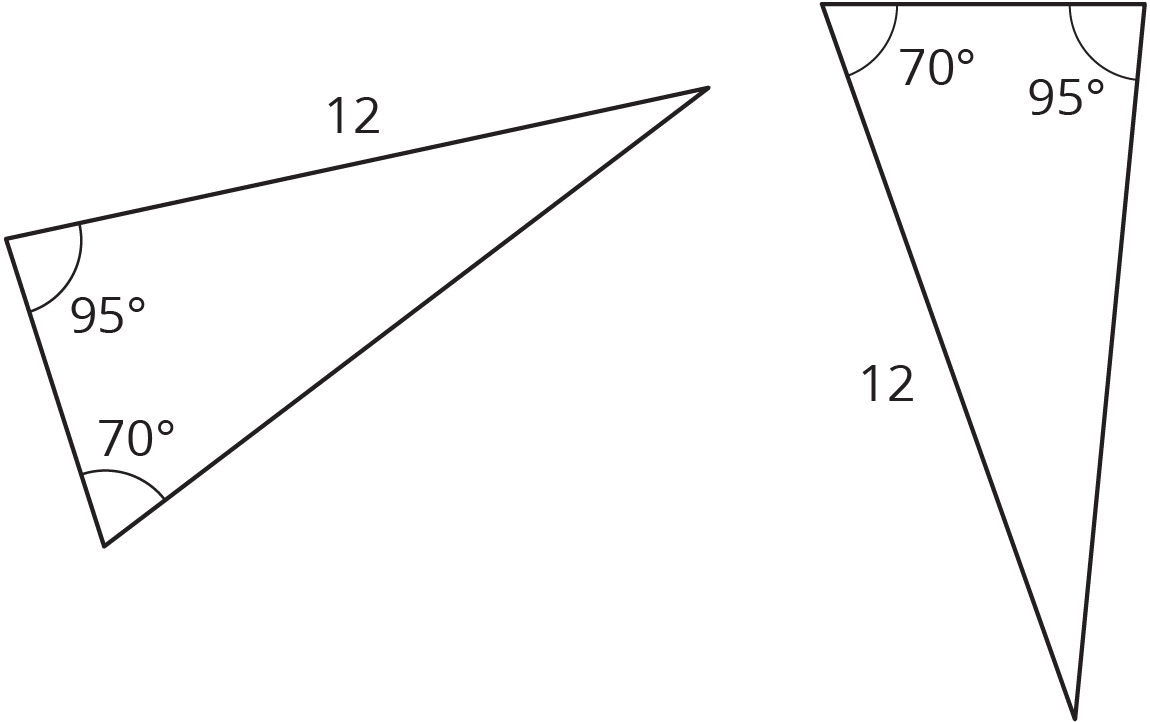
Are these two triangles identical? Explain how you know.
Problem 2
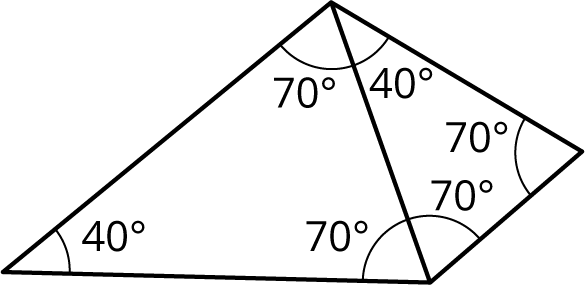
Are these triangles identical? Explain your reasoning.
Problem 3
Problem 4 (from Unit 5, Lesson 8)
The markings on the number line are equally spaced. Label the other markings on the number line.

Problem 5 (from Unit 5, Lesson 9)
A passenger on a ship dropped his camera into the ocean. If it is descending at a rate of -4.2 meters per second, how long until it hits the bottom of the ocean, which is at -1,875 meters?
Problem 6 (from Unit 4, Lesson 3)
Apples cost \$1.99 per pound.
- How much do $3 \frac{1}{4}$ pounds of apples cost?
- How much do $x$ pounds of apples cost?
- Clare spent \$5.17 on apples. How many pounds of apples did Clare buy?
Problem 7 (from Unit 3, Lesson 5)
Diego has a glue stick with a diameter of 0.7 inches. He sets it down 3.5 inches away from the edge of the table, but it rolls onto the floor. How many rotations did the glue stick make before it fell off of the table?
Lesson 9
Problem 1
Use a protractor to try to draw each triangle. Which of these three triangles is impossible to draw?
- A triangle where one angle measures $20^\circ$ and another angle measures $45^\circ$
- A triangle where one angle measures $120^\circ$ and another angle measures $50^\circ$
-
A triangle where one angle measures $90^\circ$ and another angle measures $100^\circ$
Problem 2
A triangle has an angle measuring $90^\circ$, an angle measuring $20^\circ$, and a side that is 6 units long. The 6-unit side is in between the $90^\circ$ and $20^\circ$ angles.
- Sketch this triangle and label your sketch with the given measures.
- How many unique triangles can you draw like this?
Problem 3 (from Unit 5, Lesson 13)
- Find a value for $x$ that makes $\text-x$ less than $2x$.
- Find a value for $x$ that makes $\text-x$ greater than $2x$.
Problem 4 (from Unit 5, Lesson 3)
One of the particles in atoms is called an electron. It has a charge of -1. Another particle in atoms is a proton. It has charge of +1.
The overall charge of an atom is the sum of the charges of the electrons and the protons. Here is a list of common elements.
| charge from electrons |
charge from protons |
overall charge |
|
|---|---|---|---|
| carbon | -6 | +6 | 0 |
| aluminum | -10 | +13 | |
| phosphide | -18 | +15 | |
| iodide | -54 | +53 | |
| tin | -50 | +50 |
Find the overall charge for the rest of the atoms on the list.
Problem 5 (from Unit 4, Lesson 3)
A factory produces 3 bottles of sparkling water for every 7 bottles of plain water. If those are the only two products they produce, what percentage of their production is sparkling water? What percentage is plain?
Lesson 10
Problem 1
A triangle has sides of length 7 cm, 4 cm, and 5 cm. How many unique triangles can be drawn that fit that description? Explain or show your reasoning.
Problem 2
A triangle has one side that is 5 units long and an adjacent angle that measures $25^\circ$. The two other angles in the triangle measure $90^\circ$ and $65^\circ$. Complete the two diagrams to create two different triangles with these measurements. 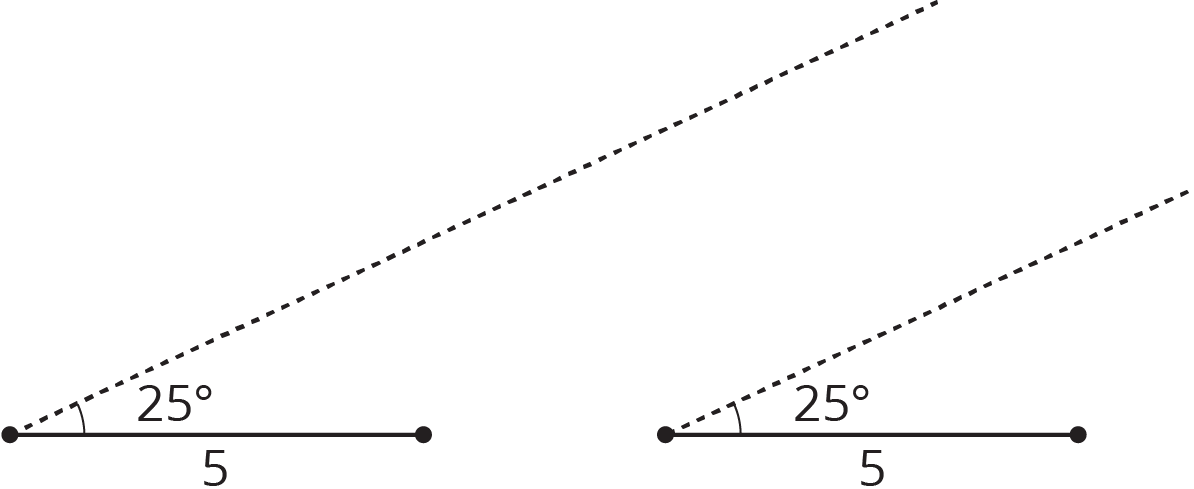
Problem 3
Is it possible to make a triangle that has angles measuring 90 degrees, 30 degrees, and 100 degrees? If so, draw an example. If not, explain your reasoning.
Problem 4 (from Unit 7, Lesson 2)
Segments $CD$, $AB$, and $FG$ intersect at point $E$. Angle $FEC$ is a right angle. Identify any pairs of angles that are complementary.

Problem 5 (from Unit 5, Lesson 15)
Match each equation to a step that will help solve the equation for $x$.
- $3x=\text-4$
- $\text-4.5 = x-3$
- $3=\frac {\text{-}x}{3}$
- $\frac13=\text-3x$
- $x-\frac{1}{3}=0.4$
- $3+x=8$
- $\frac{x}{3}=15$
- $7=\frac{1}{3}+x$
- Add $\frac13$ to each side.
- Add $\frac {\text{-}1}{3}$ to each side.
- Add $3$ to each side.
- Add $\text-3$ to each side.
- Multiply each side by 3.
- Multiply each side by $\text-3$.
- Multiply each side by $\frac13$.
- Multiply each side by $\frac {\text{-}1}{3}$.
Problem 6 (from Unit 4, Lesson 8)
- If you deposit \$300 in an account with a 6% interest rate, how much will be in your account after 1 year?
- If you leave this money in the account, how much will be in your account after 2 years?
Lesson 11
Problem 1
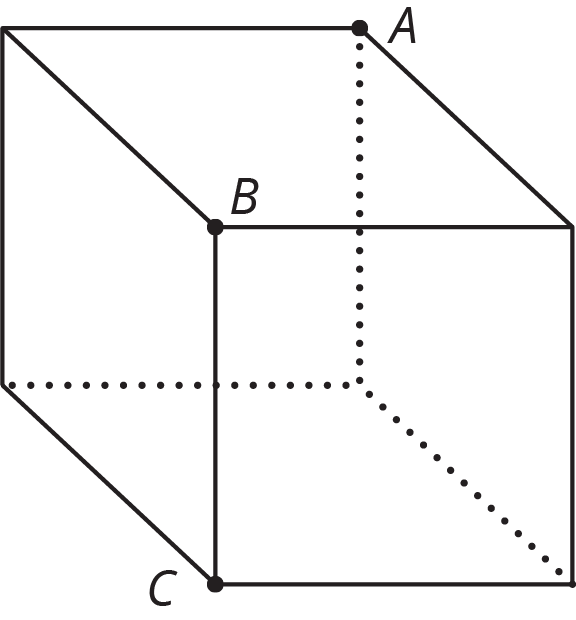
A cube is cut into two pieces by a single slice that passes through points $A$, $B$, and $C$. What shape is the cross section?
Problem 2
Describe how to slice the three-dimensional figure to result in each cross section.
Three-dimensional figure:
Cross sections:
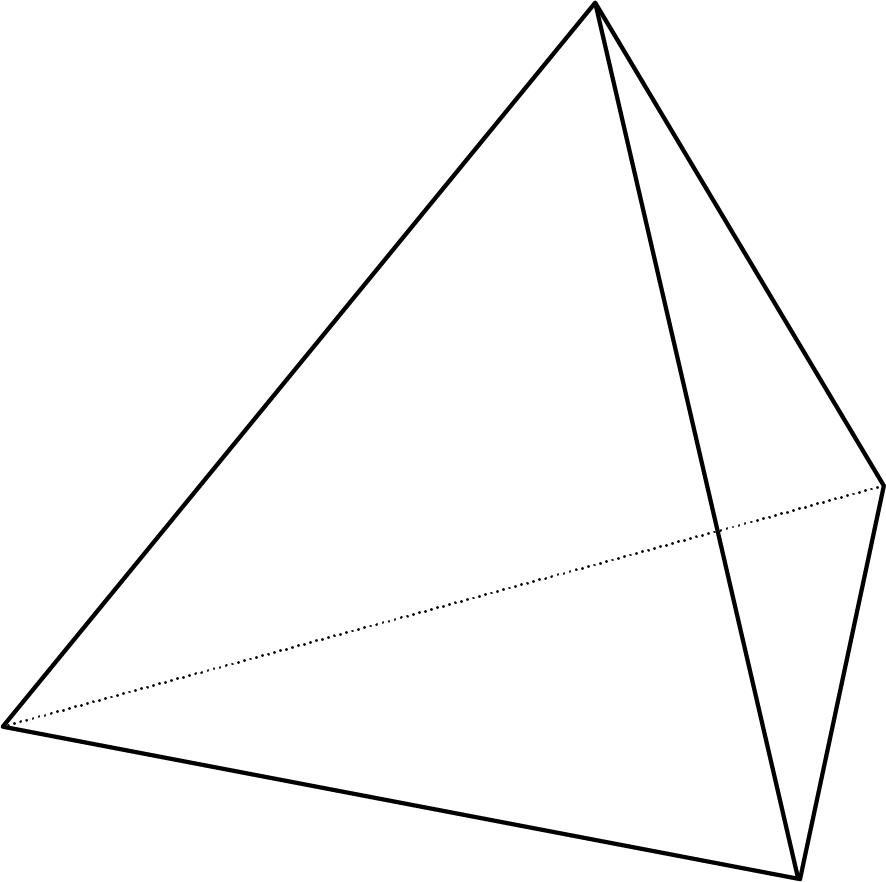

Problem 3
Here are two three-dimensional figures. 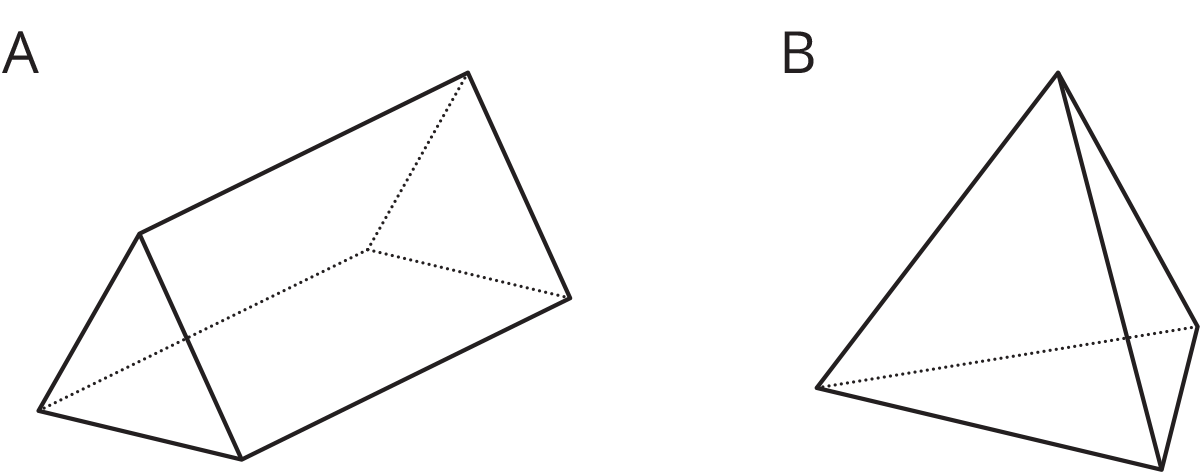
Problem 4 (from Unit 7, Lesson 2)
Each row contains the degree measures of two supplementary angles. Complete the table.
| measure of an angle |
measure of its supplement |
|
|---|---|---|
| row 1 | $80^\circ$ | |
| row 2 | $25^\circ$ | |
| row 3 | $119^\circ$ | |
| row 4 | $x$ |
Problem 5 (from Unit 4, Lesson 8)
Two months ago, the price, in dollars, of a cell phone was $c$.
- Last month, the price of the phone increased by 10%. Write an expression for the price of the phone last month.
- This month, the price of the phone decreased by 10%. Write an expression for the price of the phone this month.
- Is the price of the phone this month the same as it was two months ago? Explain your reasoning.
Lesson 12
Problem 1
- Select all the prisms.
- For each prism, shade one of its bases.
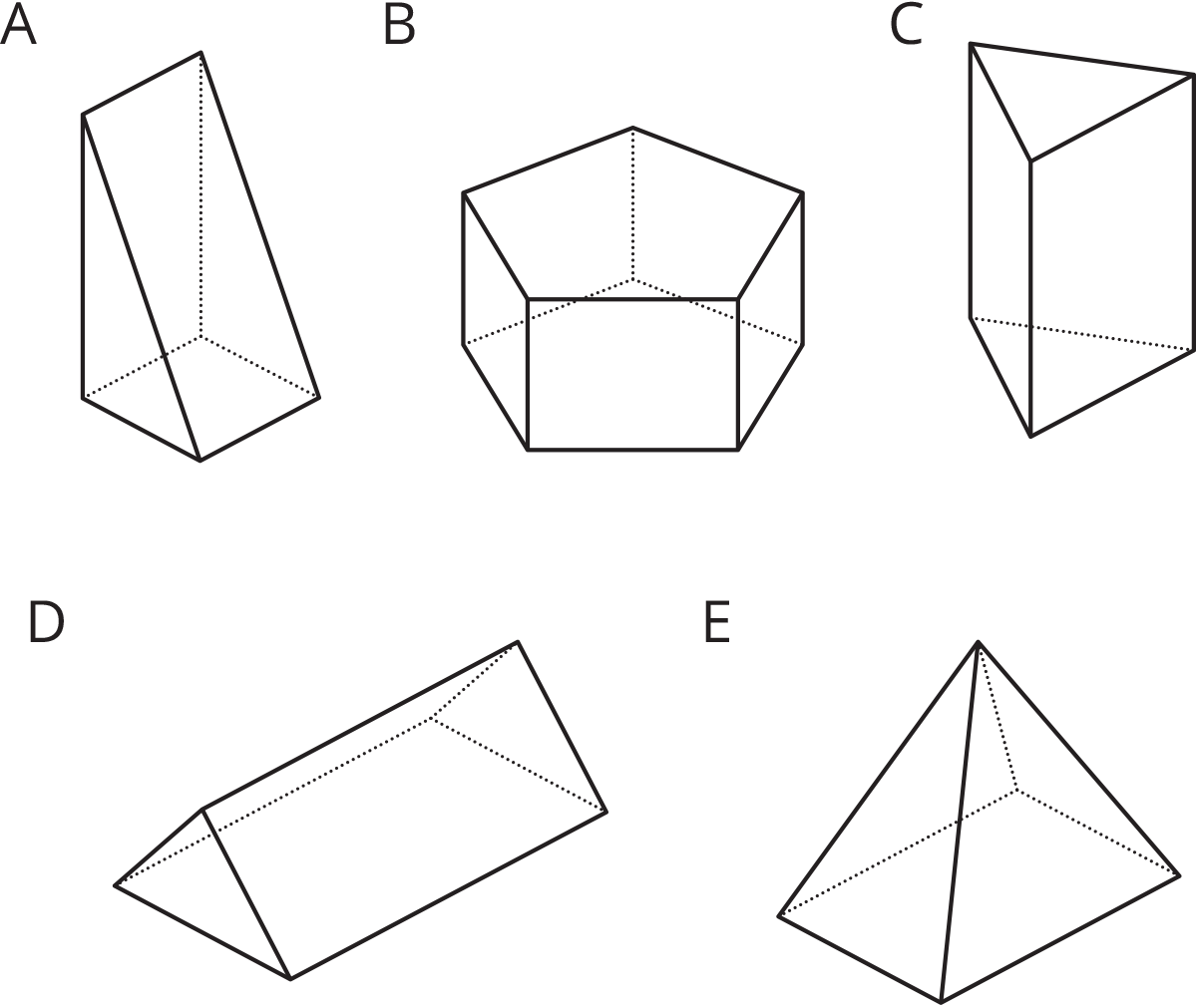
Problem 2
Problem 3 (from Unit 7, Lesson 2)
Two angles are complementary. One has a measure of 19 degrees. What is the measure of the other?
Problem 4 (from Unit 7, Lesson 2)
Two angles are supplementary. One has a measure that is twice as large as the other. Find the two angle measures.
Problem 5 (from Unit 6, Lesson 22)
Match each expression in the first list with an equivalent expression from the second list.
- $7(x+2) - x + 3$
- $6x + 3 + 4x + 5$
- $\frac {\text{-}2}{5}x - 7 + \frac35x - 3$
- $8x - 5 + 4 - 9$
- $24x + 36$
- $\frac15x -10$
- $6x+17$
- $2(5x+4)$
- $12(2x+3)$
- $8x +(\text-5) + 4 + (\text-9)$
Problem 6 (from Unit 4, Lesson 8)
Clare paid 50% more for her notebook than Priya paid for hers. Priya paid $x$ for her notebook and Clare paid $y$ dollars for hers. Write an equation that represents the relationship between $y$ and $x$.
Lesson 13
Problem 1
You find a crystal in the shape of a prism. Find the volume of the crystal.
The point $B$ is directly underneath point $E$, and the following lengths are known:
- From $A$ to $B$: 2 mm
- From $B$ to $C$: 3 mm
- From $A$ to $F$: 6 mm
- From $B$ to $E$: 10 mm
- From $C$ to $D$: 7 mm
- From $A$ to $G$: 4 mm
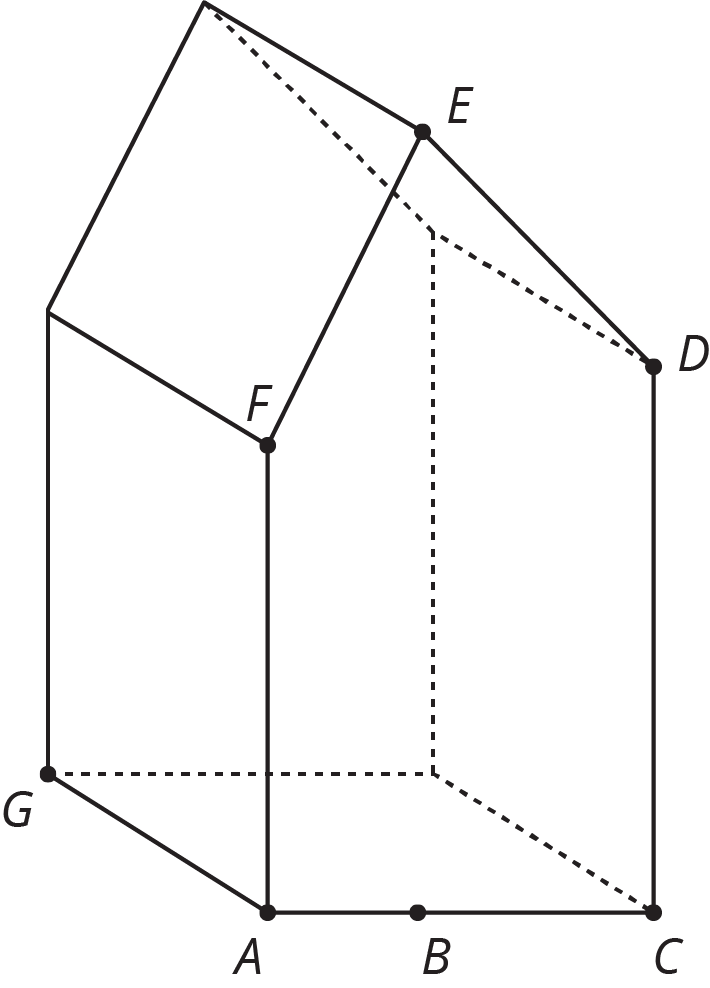
Problem 2
A rectangular prism with dimensions 5 inches by 13 inches by 10 inches was cut to leave a piece as shown in the image. What is the volume of this piece? What is the volume of the other piece not pictured?
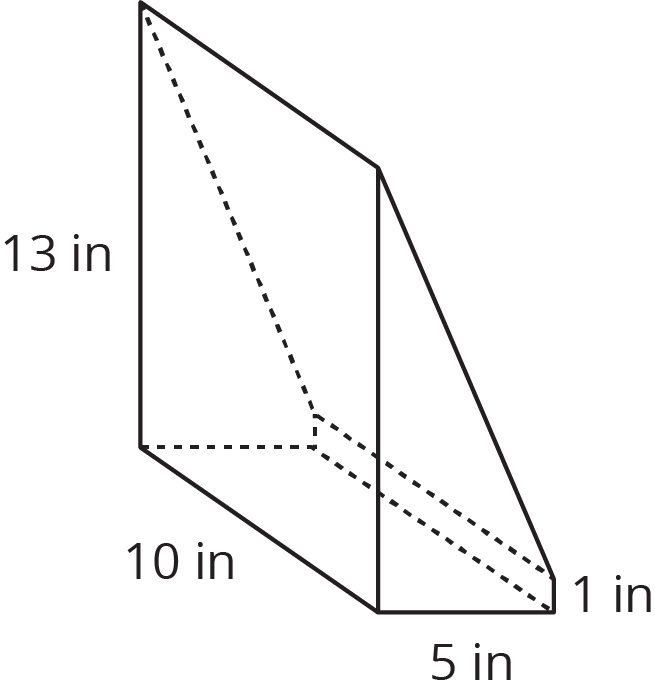
Problem 3 (from Unit 7, Lesson 9)
A triangle has one side that is 7 cm long and another side that is 3 cm long.
- Sketch this triangle and label your sketch with the given measures. (If you are stuck, try using a compass or cutting some straws to these two lengths.)
- Draw one more triangle with these measures that is not identical to your first triangle.
- Explain how you can tell they are not identical.
Problem 4 (from Unit 7, Lesson 4)
Select all equations that represent a relationship between angles in the figure.
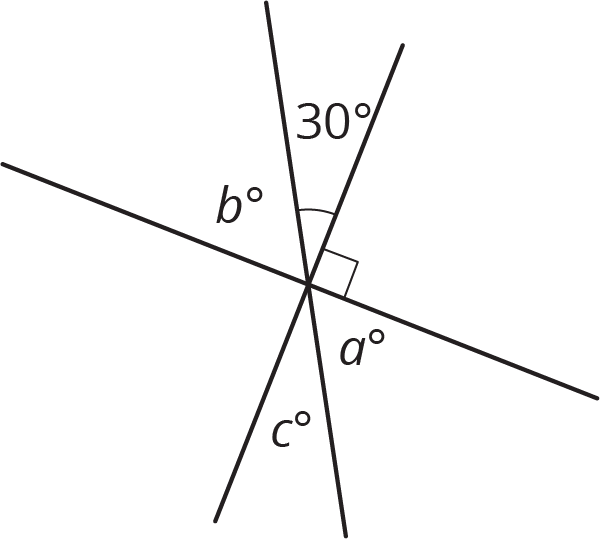
- $90-30=b$
- $30+b=a+c$
- $a+c+30+b=180$
- $a=30$
- $a=c=30$
- $90+a+c=180$
Problem 5 (from Unit 4, Lesson 9)
A mixture of punch contains 1 quart of lemonade, 2 cups of grape juice, 4 tablespoons of honey, and $\frac12$ gallon of sparkling water. Find the percentage of the punch mixture that comes from each ingredient. Round your answers to the nearest tenth of a percent. (Hint: 1 cup = 16 tablespoons)
Lesson 14
Problem 1
Edge lengths are given in units. Find the surface area of each prism in square units.
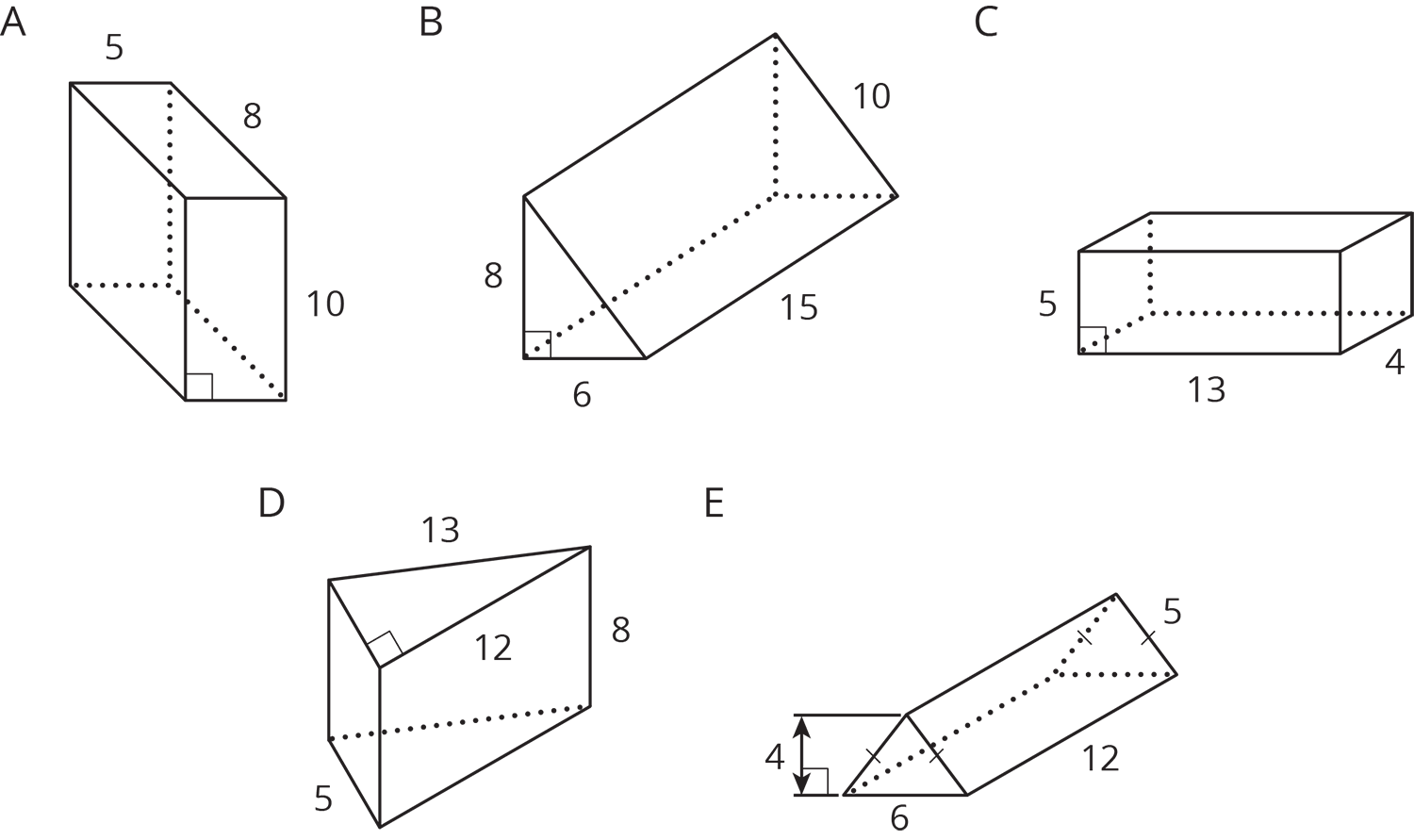
Problem 2 (from Unit 7, Lesson 11)
Priya says, “No matter which way you slice this rectangular prism, the cross section will be a rectangle.” Mai says, “I’m not so sure.” Describe a slice that Mai might be thinking of.

Problem 3 (from Unit 7, Lesson 5)
$B$ is the intersection of line $AC$ and line $ED$. Find the measure of each of the angles.
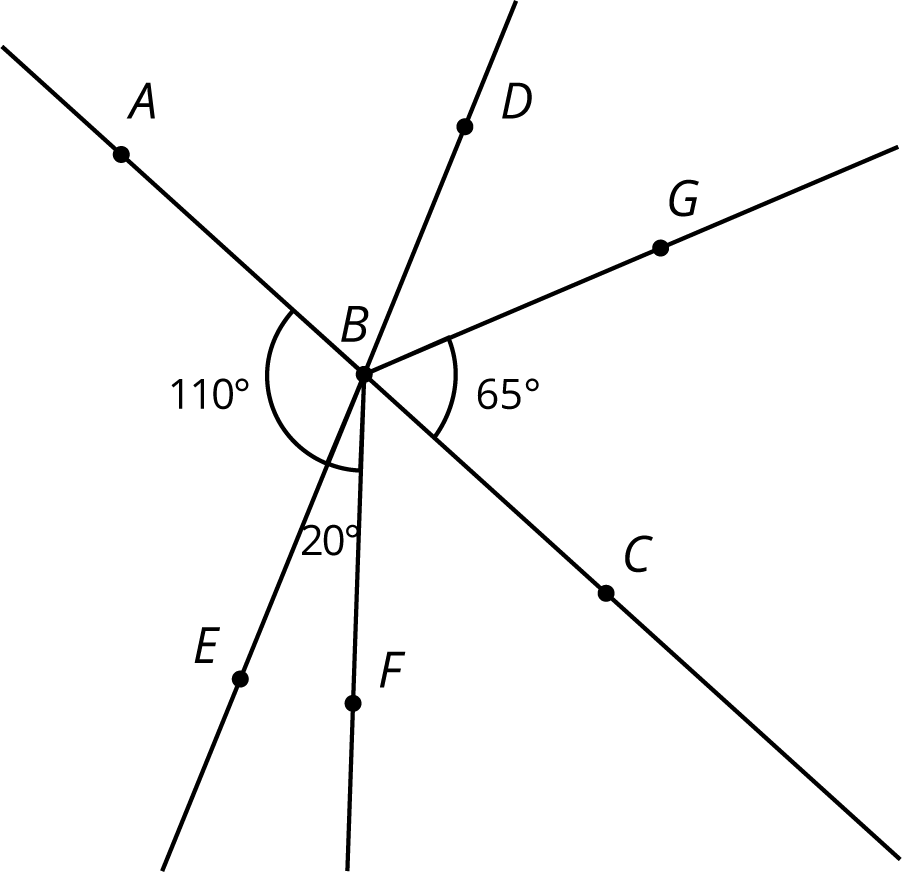
-
The measure of angle $ABF$
-
The measure of angle $ABD$
-
The measure of angle $EBC$
-
The measure of angle $FBC$
-
The measure of angle $DBG$
Problem 4 (from Unit 6, Lesson 20)
Write each expression with fewer terms.
- $12m-4m$
- $12m-5k+m$
- $9m+ k-(3m-2k)$
Problem 5 (from Unit 4, Lesson 9)
- Find 44% of 625 using the facts that 40% of 625 is 250 and 4% of 625 is 25.
- What is 4.4% of 625?
- What is 0.44% of 625?
Lesson 15
Problem 1
Here is the base of a prism.
-
If the height of the prism is 5 cm, what is its surface area? What is its volume?
-
If the height of the prism is 10 cm, what is its surface area? What is its volume?
-
When the height doubled, what was the percent increase for the surface area? For the volume?
Problem 2
Select all the situations where knowing the volume of an object would be more useful than knowing its surface area.
-
Determining the amount of paint needed to paint a barn.
-
Determining the monetary value of a piece of gold jewelry.
-
Filling an aquarium with buckets of water.
-
Deciding how much wrapping paper a gift will need.
-
Packing a box with watermelons for shipping.
-
Charging a company for ad space on your race car.
-
Measuring the amount of gasoline left in the tank of a tractor.
Problem 3 (from Unit 7, Lesson 9)
Han draws a triangle with a $50^\circ$ angle, a $40^\circ$ angle, and a side of length 4 cm as shown. Can you draw a different triangle with the same conditions?

Problem 4 (from Unit 7, Lesson 3)
Angle $H$ is half as large as angle $J$. Angle $J$ is one fourth as large as angle $K$. Angle $K$ has measure 240 degrees. What is the measure of angle $H$?
Problem 5 (from Unit 4, Lesson 9)
The Colorado state flag consists of three horizontal stripes of equal height. The side lengths of the flag are in the ratio $2:3$. The diameter of the gold-colored disk is equal to the height of the center stripe. What percentage of the flag is gold?

Lesson 16
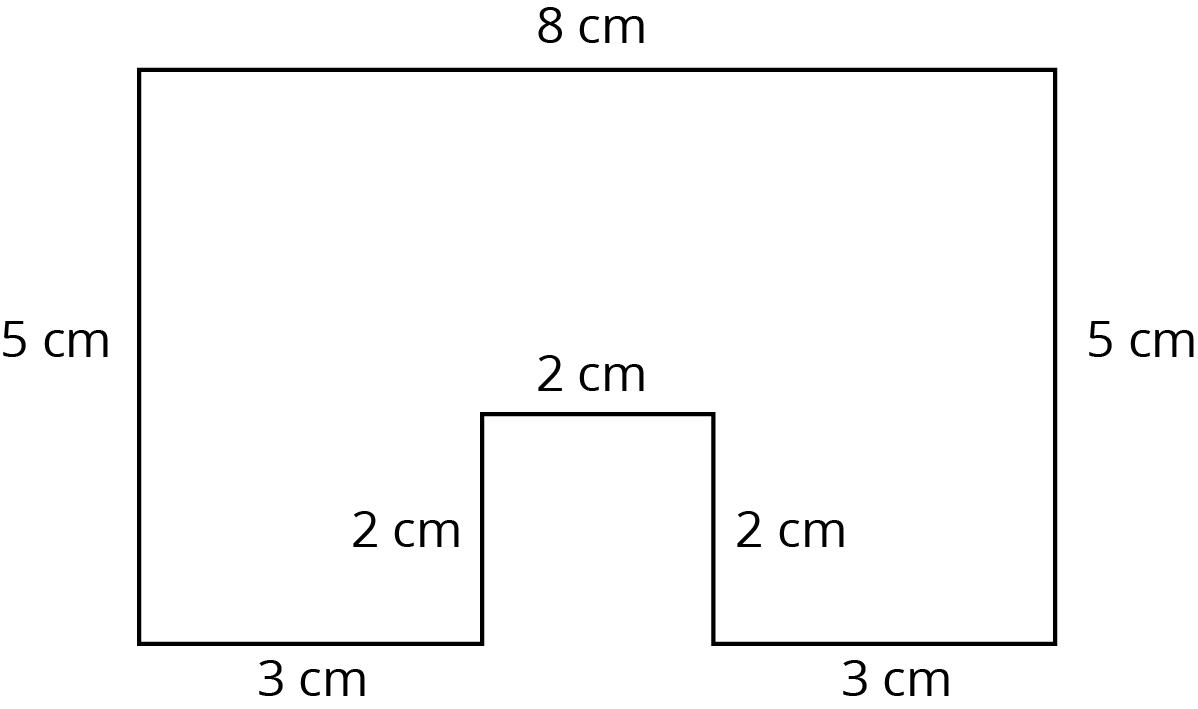
Problem 1
A landscape architect is designing a pool that has this top view: 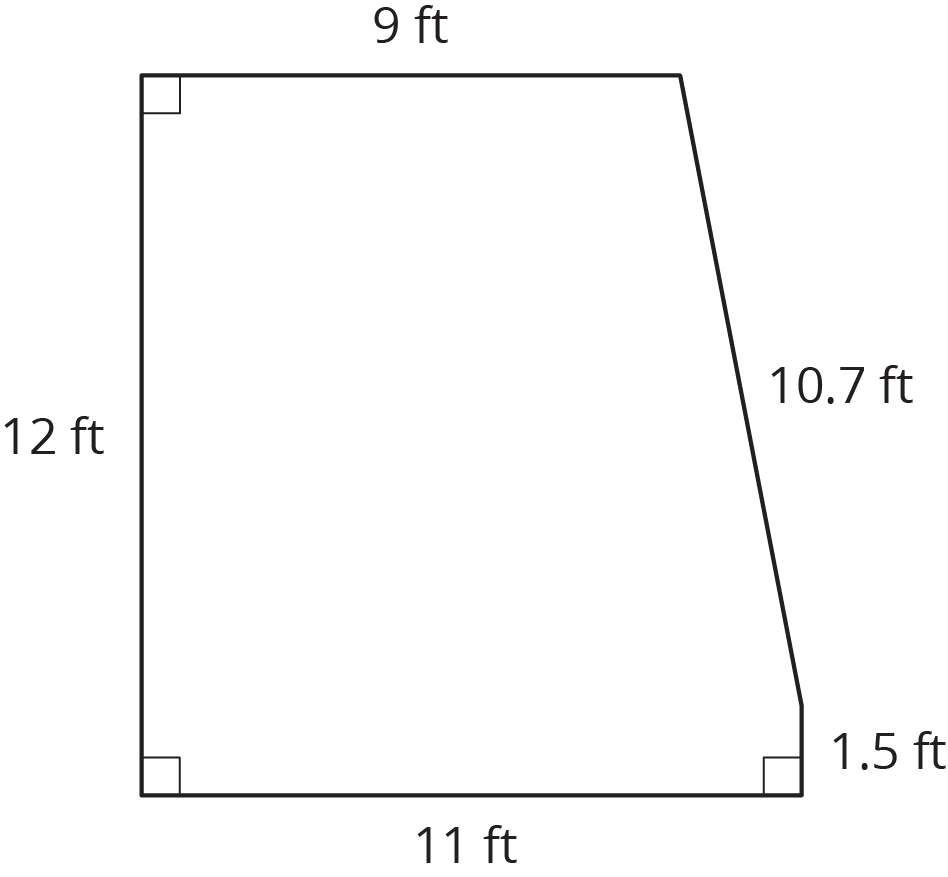
- How much water will be needed to fill this pool 4 feet deep?
- Before filling up the pool, it gets lined with a plastic liner. How much liner is needed for this pool?
- Here are the prices for different amounts of plastic liner. How much will all the plastic liner for the pool cost?
plastic liner (ft2) cost ($) row 1 25 3.75 row 2 50 7.50 row 3 75 11.25
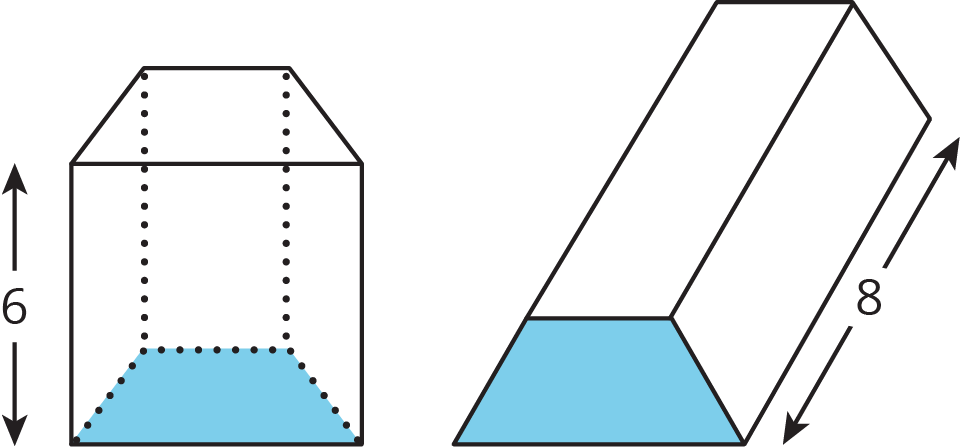
Problem 2 (from Unit 7, Lesson 13)
Shade in a base of the trapezoidal prism. (Be careful! The base is not the same as the bottom.)
- Find the area of the base you shaded.
- Find the volume of this trapezoidal prism.
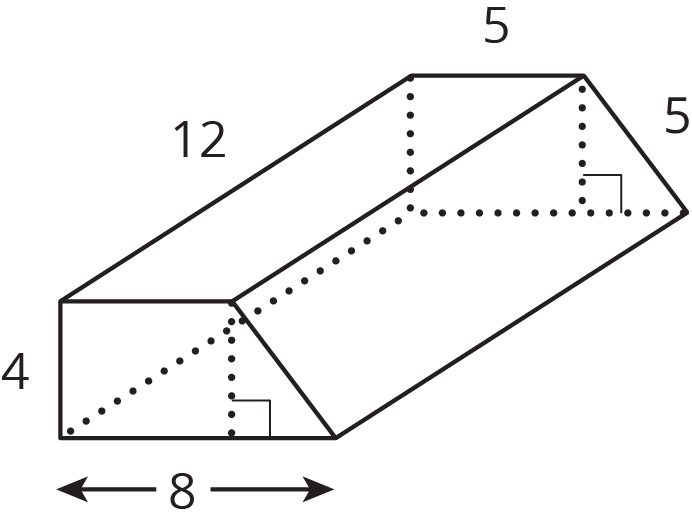
Problem 3 (from Unit 4, Lesson 9)
For each diagram, decide if $y$ is an increase or a decrease of $x$. Then determine the percentage that $x$ increased or decreased to result in $y$.
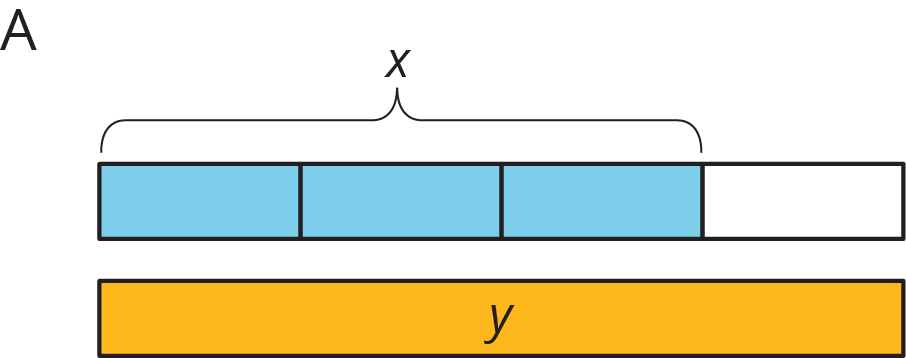
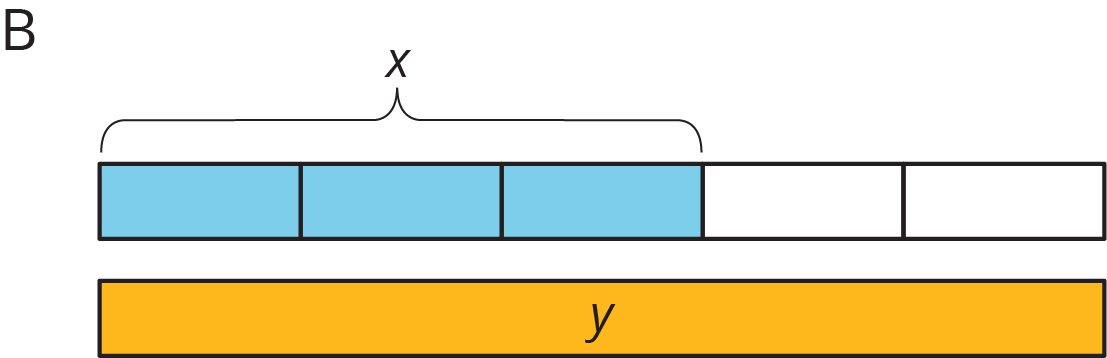
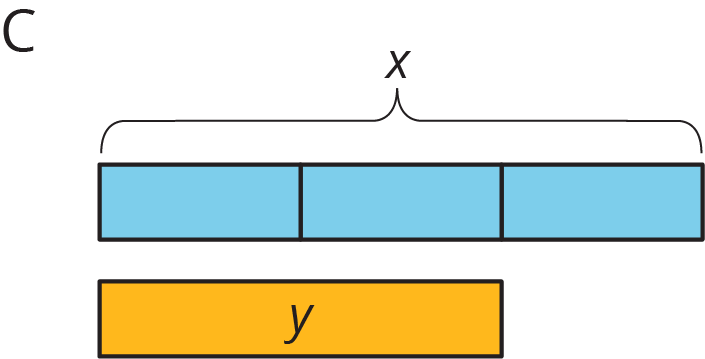
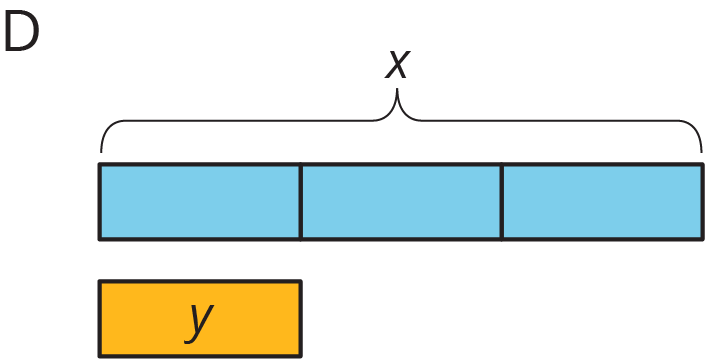
Problem 4 (from Unit 4, Lesson 10)
Noah is visiting his aunt in Texas. He wants to buy a belt buckle whose price is \$25. He knows that the sales tax in Texas is 6.25%.
- How much will the tax be on the belt buckle?
- How much will Noah spend for the belt buckle including the tax?
- Write an equation that represents the total cost, $c$, of an item whose price is $p$.
Lesson 17
No practice problems for this lesson.