Lesson 11: Comparing Groups

Let’s compare two groups.

11.1: Notice and Wonder: Comparing Heights

What do you notice? What do you wonder?

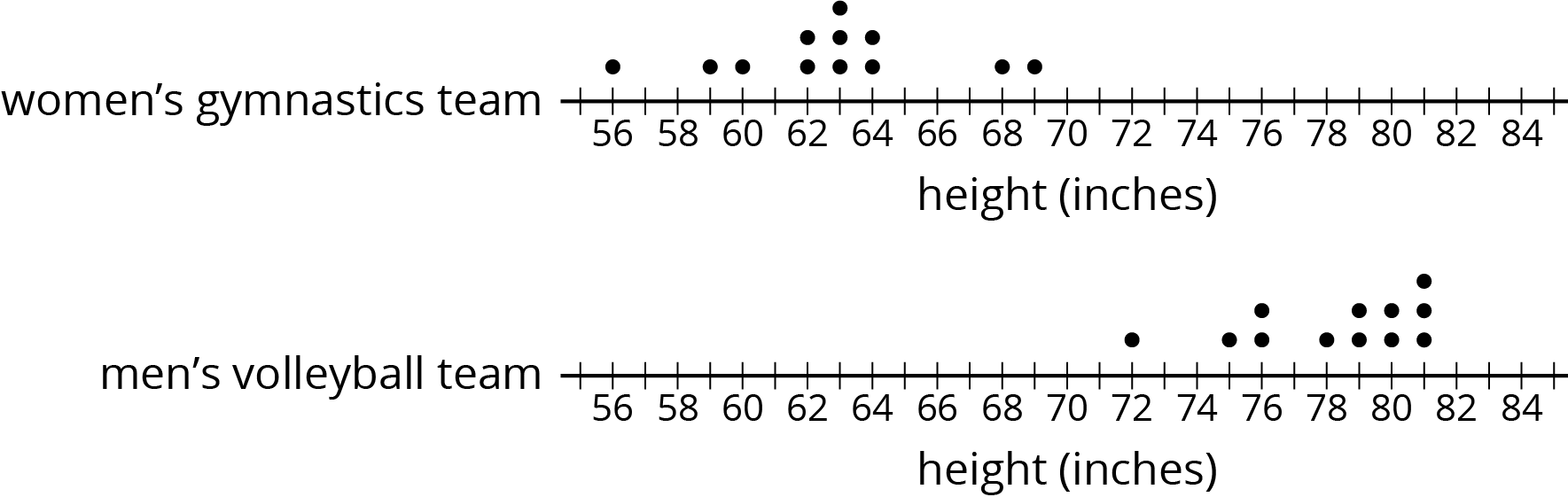
Two dot plots for “height in inches” are labeled “women’s gymnastics team” and “men’s volleyball team.” The numbers 56 through 84, in increments of 2, are indicated on both dot plots. The data are as follows: Women’s gymnastics team: 56 inches, 1 dot. 59 inches, 1 dot. 60 inches, 1 dot. 62 inches, 2 dots. 63 inches, 3 dots. 64 inches, 2 dots. 68 inches, 1 dot. 69 inches, 1 dot. Men’s volleyball team: 72 inches, 1 dot. 75 inches, 1 dot. 76 inches, 2 dots. 78 inches, 1 dot. 79 inches, 2 dots. 80 inches, 2 dots. 81 inches, 3 dots.

11.2: More Team Heights

  1. How much taller is the volleyball team than the gymnastics team?

    • Gymnastics team’s heights (in inches) : 56, 59, 60, 62, 62, 63, 63, 63, 64, 64, 68, 69

    • Volleyball team’s heights (in inches): 72, 75, 76, 76, 78, 79, 79, 80, 80, 81, 81, 81

  2. Make dot plots to compare the heights of the tennis and badminton teams.

    • Tennis team’s heights (in inches): 66, 67, 69, 70, 71, 73, 73, 74, 75, 75, 76

    • Badminton team’s heights (in inches): 62, 62, 65, 66, 68, 71, 73

    What do you notice about your dot plots?

  3. Elena says the members of the tennis team were taller than the badminton team. Lin disagrees. Do you agree with either of them? Explain or show your reasoning.

11.3: Family Heights

Compare the heights of these two families. Explain or show your reasoning.

  • The heights (in inches) of Noah’s family members: 28, 39, 41, 52, 63, 66, 71

  • The heights (in inches) of Jada’s family members: 49, 60, 68, 70, 71, 73, 77

11.4: Track Length

Here are three dot plots that represent the lengths, in minutes, of songs on different albums.

A dot plot labeled “A.” The numbers 0 through 7, in increments of 0 point 5, are indicated. The data are as follows: 5, 2 dots. 5 point 25, 1 dot. 5 point 5, 1 dot. 5 point 75, 1 dot. 6, 1 dot. 6 point 5, 1 dot.
 
A dot plot labeled “B.” The numbers 0 through 7, in increments of 0 point 5, are indicated. The data are as follows: 0 point 5, 1 dot. 0 point 7 5, 1 dot. 1 point 5, 2 dots. 2, 1 dot. 3 point 7 5, 1 dot. 4 point 2 5, 1 dot. 5, 1 dot.
 
A dot plot labeled “C.” The numbers 0 through 7, in increments of 0 point 5, are indicated. The data are as follows: 3 point 5, 3 dots. 4, 3 dots. 4 point 25, 1 dot. 4 point 5, 1 dot.

  1. One of these data sets has a mean of 5.57 minutes and another has a mean of 3.91 minutes.

    1. Which dot plot shows each of these data sets?
    2. Calculate the mean for the data set on the other dot plot.

  2. One of these data sets has a mean absolute deviation of 0.30 and another has a MAD of 0.44.

    1. Which dot plot shows each of these data sets?
    2. Calculate the MAD for the other data set.

  3. Do you think the three groups are very different or not? Be prepared to explain your reasoning.

  4. A fourth album has a mean length of 8 minutes with a mean absolute deviation of 1.2. Is this data set very different from each of the others?

Summary

Comparing two individuals is fairly straightforward. The question "Which dog is taller?" can be answered by measuring the heights of two dogs and comparing them directly. Comparing two groups can be more challenging. What does it mean for the basketball team to generally be taller than the soccer team?

To compare two groups, we use the distribution of values for the two groups. Most importantly, a measure of center (usually mean or median) and its associated measure of variability (usually mean absolute deviation or interquartile range) can help determine the differences between groups.

For example, if the average height of pugs in a dog show is 11 inches, and the average height of the beagles in the dog show is 15 inches, it seems that the beagles are generally taller. On the other hand, if the MAD is 3 inches, it would not be unreasonable to find a beagle that is 11 inches tall or a pug that is 14 inches tall. Therefore the heights of the two dog breeds may not be very different from one another.

Practice Problems ▶

Glossary

mean absolute deviation (MAD)

mean absolute deviation (MAD)

The mean absolute deviation measures the spread in a distribution. It is the mean of the distances of the data points from the mean of the distribution. (It is called mean absolute deviation because the distance of a data point from the mean is the absolute value of its deviation from the mean.)

mean

mean

The mean, or average, of a data set is the value you get by adding up all of the values in the set and dividing by the number of values in the set.

median

median

The median of a data set is the middle value when the data values are listed in order. If the number of values is even, it is the mean of the two middle values.

interquartile range (IQR)

interquartile range (IQR)

The interquartile range of a data set is a measure of spread of its distribution. It is the difference between the third quartile (Q3) and the first quartile (Q1).