Sometimes we want to compare two different populations. For example, is there a meaningful difference between the weights of pugs and beagles? Here are histograms showing the weights for a sample of dogs from each of these breeds:
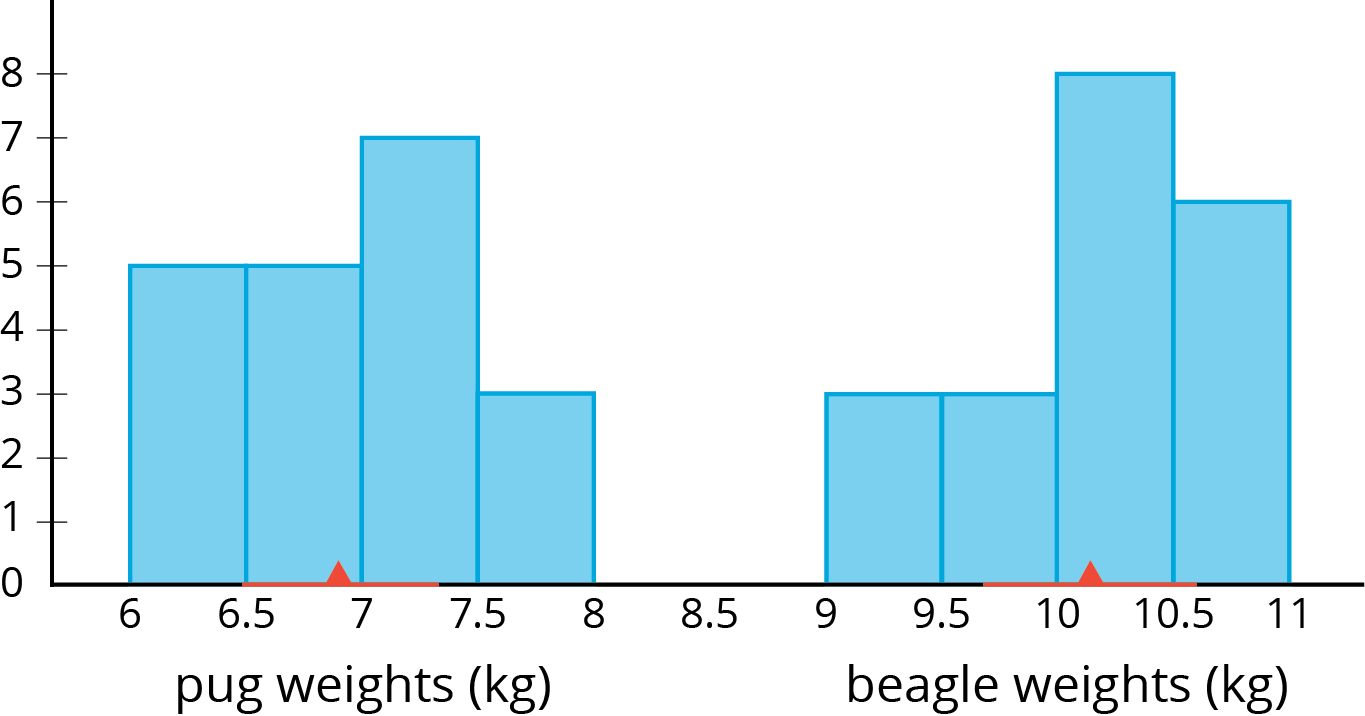
The red triangles show the mean weight of each sample, 6.9 kg for the pugs and 10.1 kg for the beagles. The red lines show the weights that are within 1 MAD of the mean. We can think of these as “typical” weights for the breed. These typical weights do not overlap. In fact, the distance between the means is $10.1-6.9 $ or 3.2 kg, over 6 times the larger MAD! So we can say there is a meaningful difference between the weights of pugs and beagles.
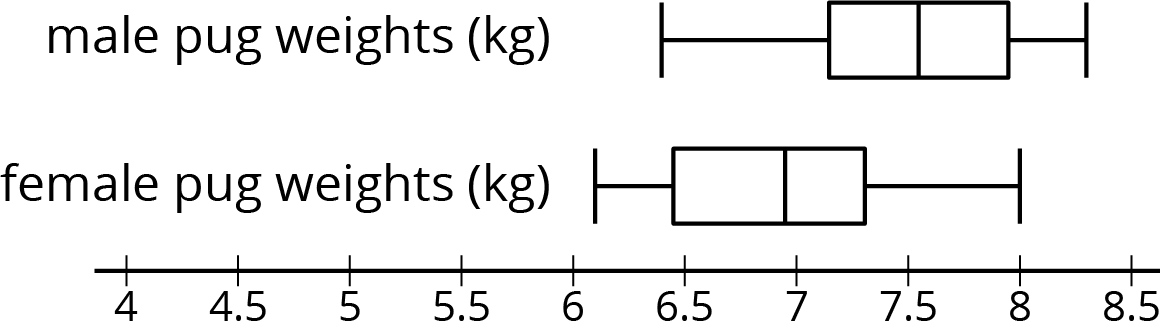
Is there a meaningful difference between the weights of male pugs and female pugs? Here are box plots showing the weights for a sample of male and female pugs:
We can see that the medians are different, but the weights between the first and third quartiles overlap. Based on these samples, we would say there is not a meaningful difference between the weights of male pugs and female pugs.
In general, if the measures of center for two samples are at least two measures of variability apart, we say the difference in the measures of center is meaningful. Visually, this means the range of typical values does not overlap. If they are closer, then we don't consider the difference to be meaningful.