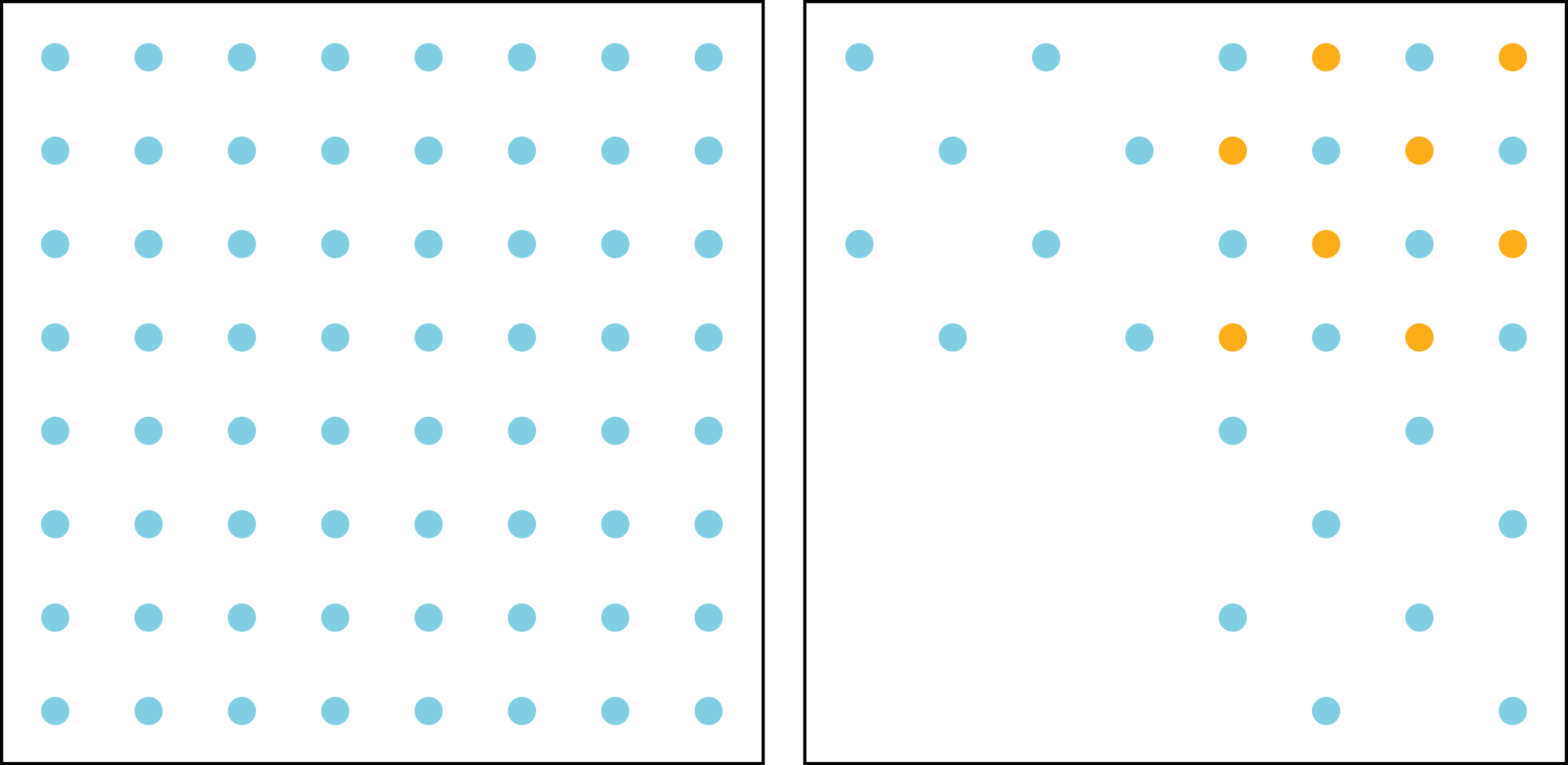5.1: Dot Density
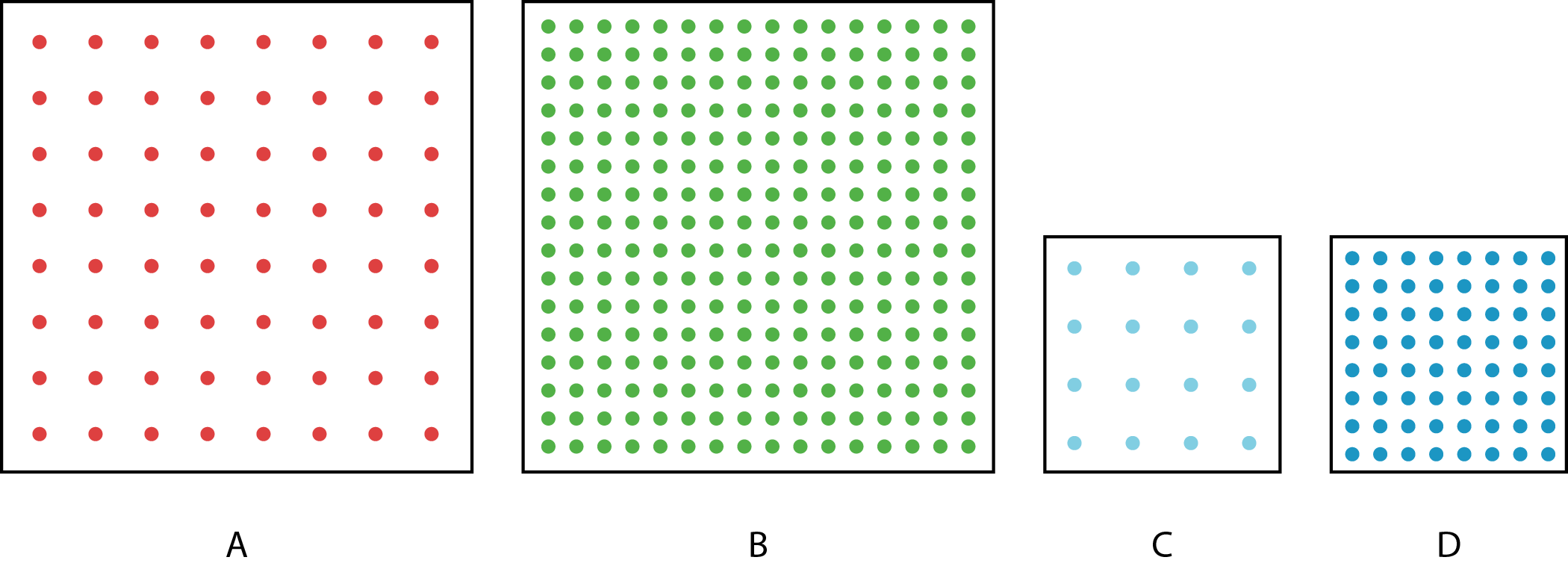
The figure shows four squares. Each square encloses an array of dots. Squares A and B have side length 2 inches. Squares C and D have side length 1 inch.
-
Complete the table with information about each square.
square area of the square
in square inchesnumber
of dotsnumber of dots
per square inchrow 1 A row 2 B row 3 C row 4 D -
Compare each square to the others. What is the same and what is different?