Earlier, we learned that if we apply a sequence of rigid transformations to a figure, then corresponding sides have equal length and corresponding angles have equal measure. These facts let us figure out things without having to measure them!
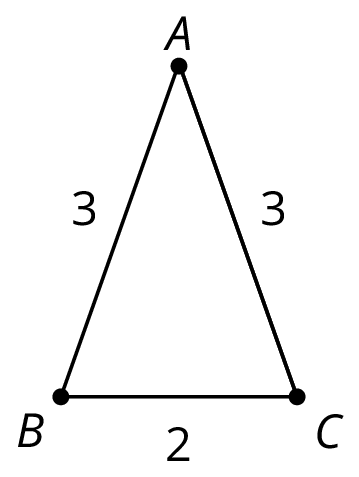
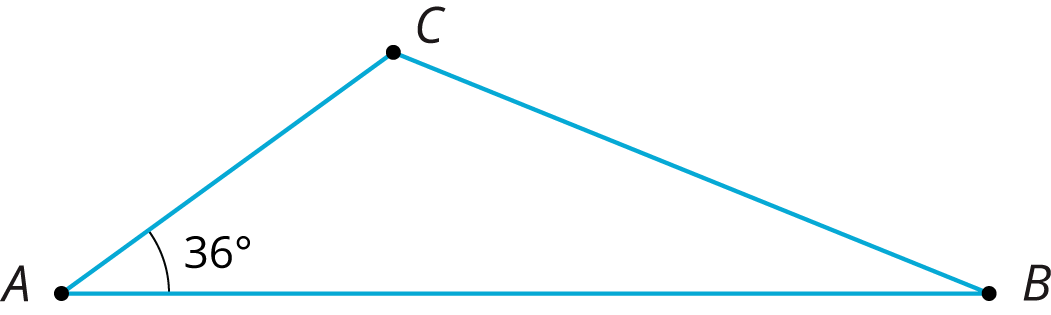
For example, here is triangle $ABC$.
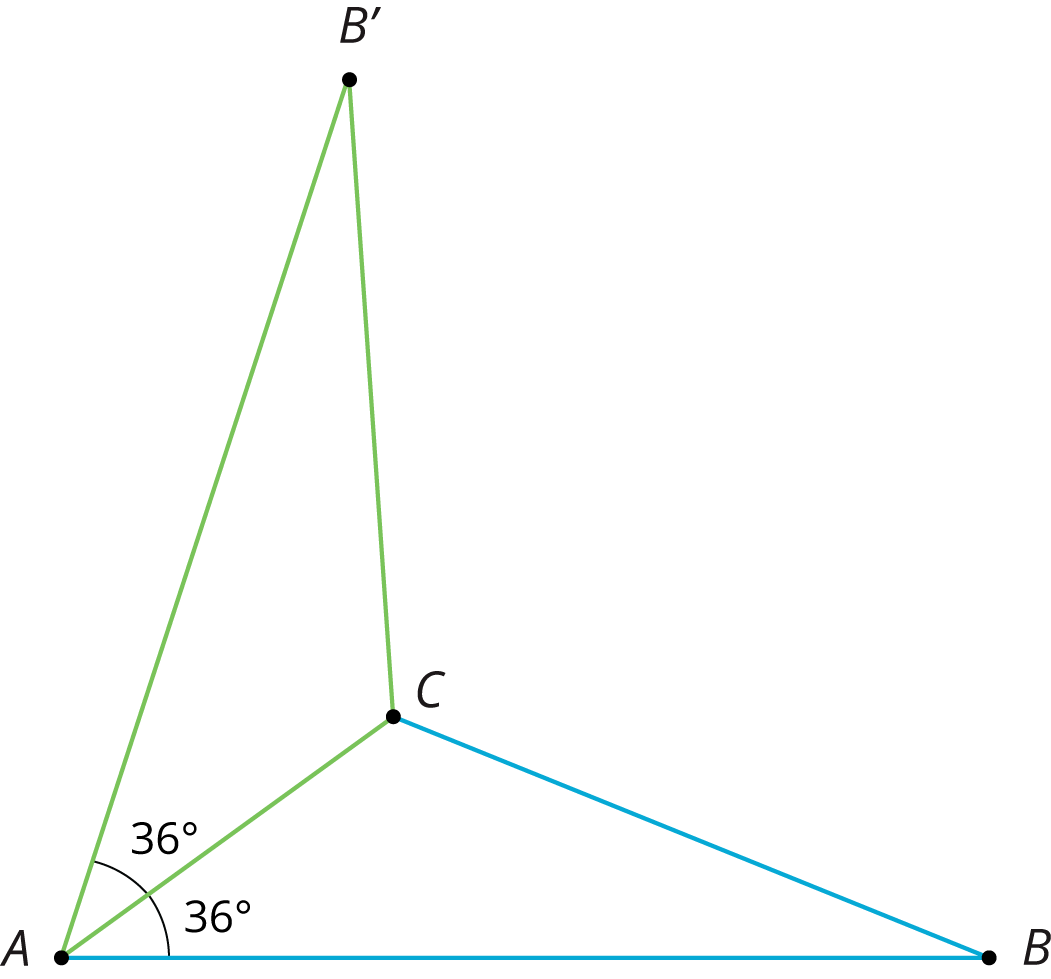
We can reflect triangle $ABC$ across side $AC$ to form a new triangle:
Because points $A$ and $C$ are on the line of reflection, they do not move. So the image of triangle $ABC$ is $AB'C$. We also know that:
- Angle $B'AC$ measures $36^\circ$ because it is the image of angle $BAC$.
- Segment $AB'$ has the same length as segment $AB$.
When we construct figures using copies of a figure made with rigid transformations, we know that the measures of the images of segments and angles will be equal to the measures of the original segments and angles.