Lesson 12: Congruent Polygons

Let’s decide if two figures are congruent.

12.1: Translated Images

All of these triangles are congruent. Sometimes we can take one figure to another with a translation. Shade the triangles that are images of triangle $ABC$ under a translation.

12.2: Congruent Pairs (Part 1)

For each of the following pairs of shapes, decide whether or not they are congruent. Explain your reasoning.

  1.  
  2.  
  3.  
  4.  

12.3: Congruent Pairs (Part 2)

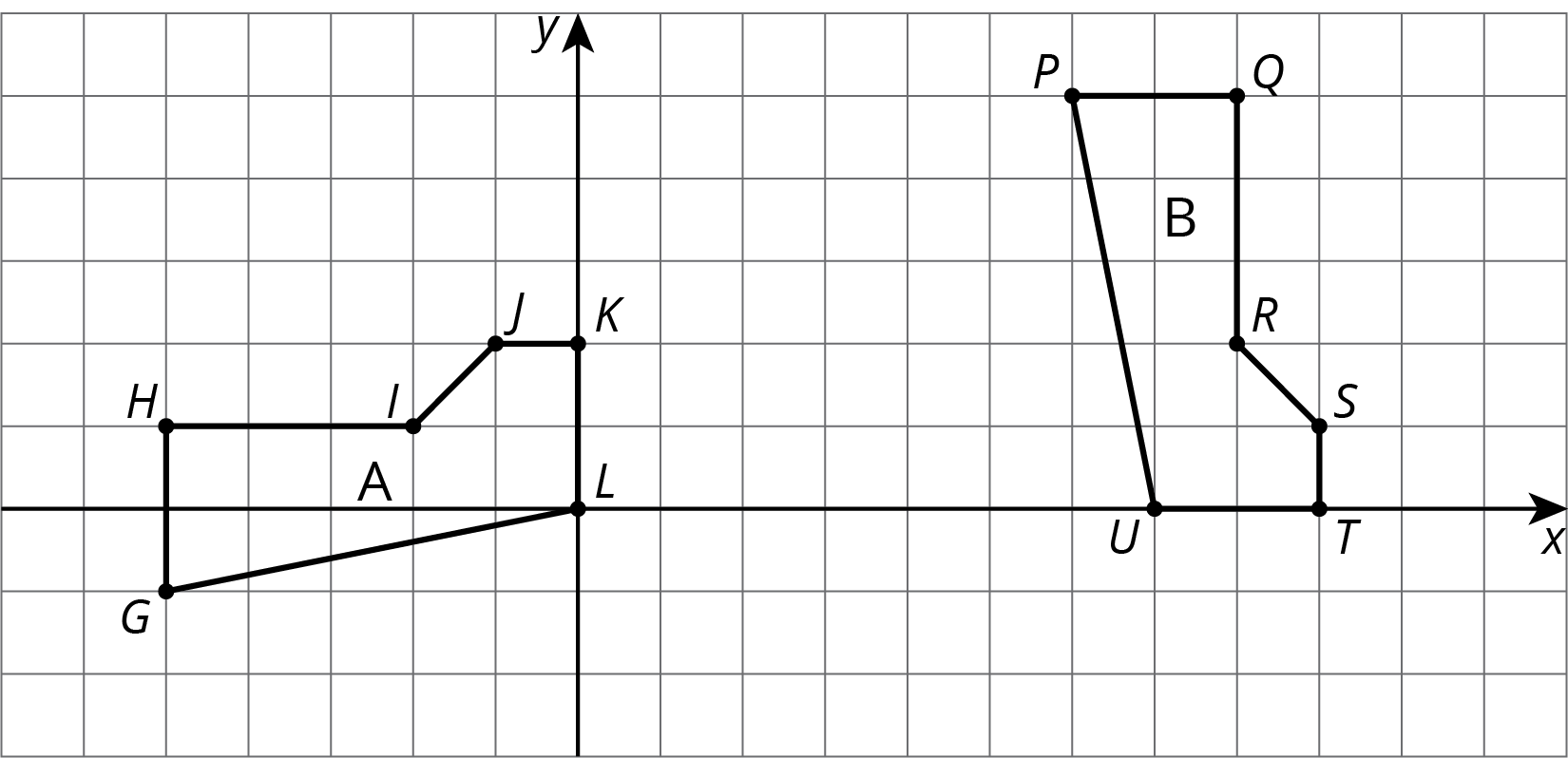
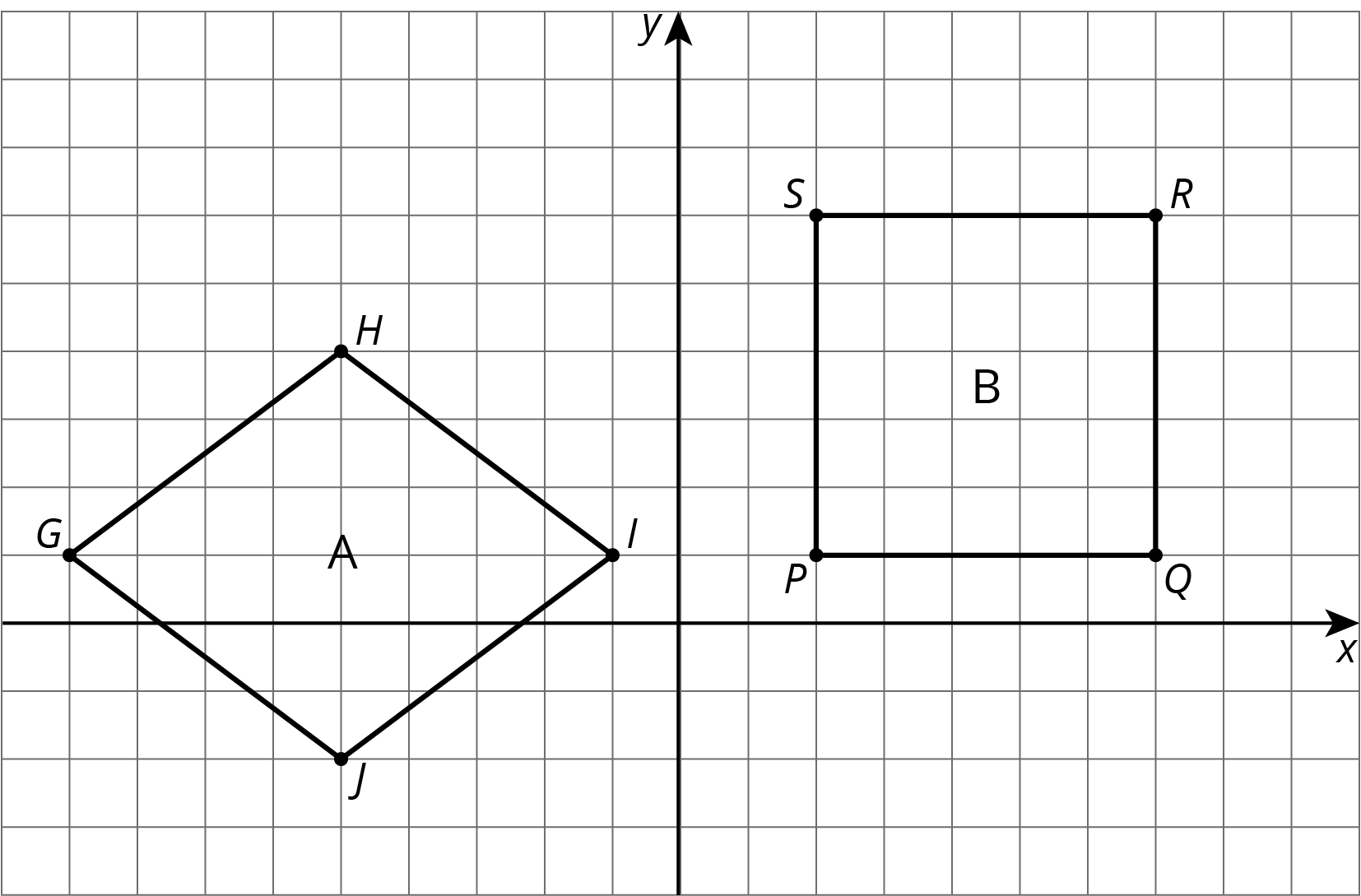
For each pair of shapes, decide whether or not Shape A is congruent to Shape B. Explain how you know.

  1.  

  2.  
  3.  

  4.  
  5.  

12.4: Building Quadrilaterals

Your teacher will give you a set of four objects.

  1. Make a quadrilateral with your four objects and record what you have made.

  2. Compare your quadrilateral with your partner’s. Are they congruent? Explain how you know.

  3. Repeat steps 1 and 2, forming different quadrilaterals. If your first quadrilaterals were not congruent, can you build a pair that is? If your first quadrilaterals were congruent, can you build a pair that is not? Explain.

Summary

How do we know if two figures are congruent?

  • If we copy one figure on tracing paper and move the paper so the copy covers the other figure exactly, then that suggests they are congruent.

  • We can prove that two figures are congruent by describing a sequence of translations, rotations, and reflections that move one figure onto the other so they match up exactly.

How do we know that two figures are not congruent?

  • If there is no correspondence between the figures where the parts have equal measure, that proves that the two figures are not congruent. In particular,

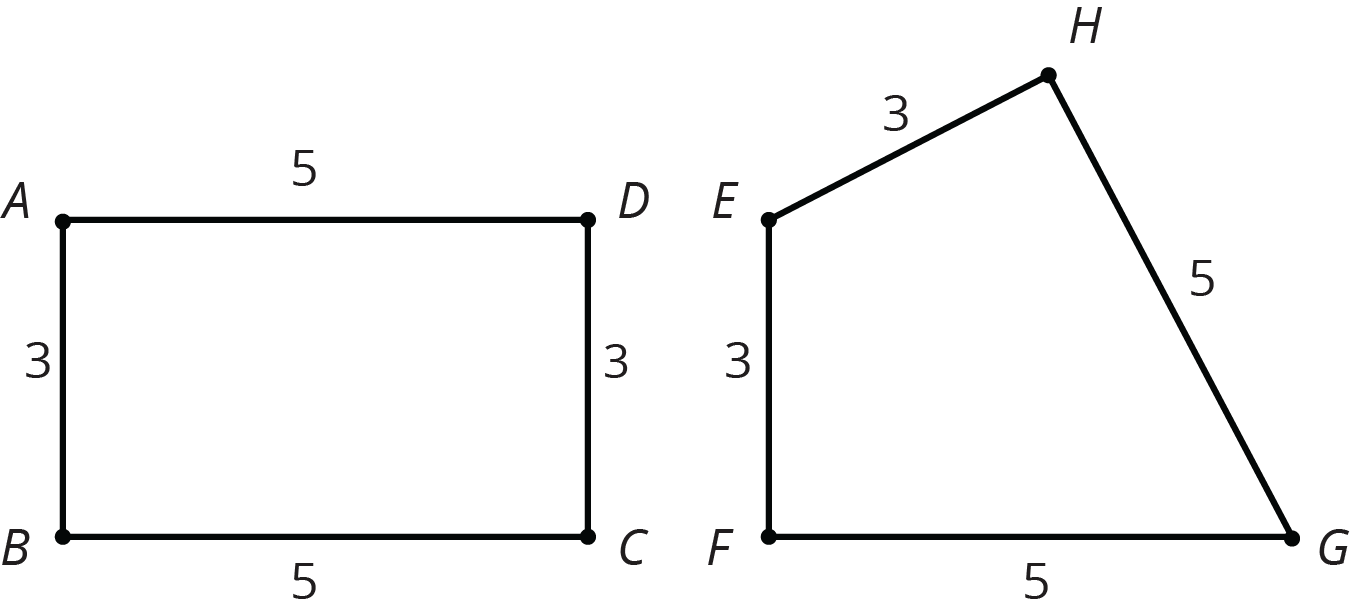
    • If two polygons have different sets of side lengths, they can’t be congruent. For example, the figure on the left has side lengths 3, 2, 1, 1, 2, 1. The figure on the right has side lengths 3, 3, 1, 2, 2, 1. There is no way to make a correspondence between them where all corresponding sides have the same length.

    • If two polygons have the same side lengths, but their orders can’t be matched as you go around each polygon, the polygons can’t be congruent. For example, rectangle $ABCD$ can’t be congruent to quadrilateral $EFGH$. Even though they both have two sides of length 3 and two sides of length 5, they don’t correspond in the same order. In $ABCD$, the order is 3, 5, 3, 5 or 5, 3, 5, 3; in $EFGH$, the order is 3, 3, 5, 5 or 3, 5, 5, 3 or 5, 5, 3, 3.

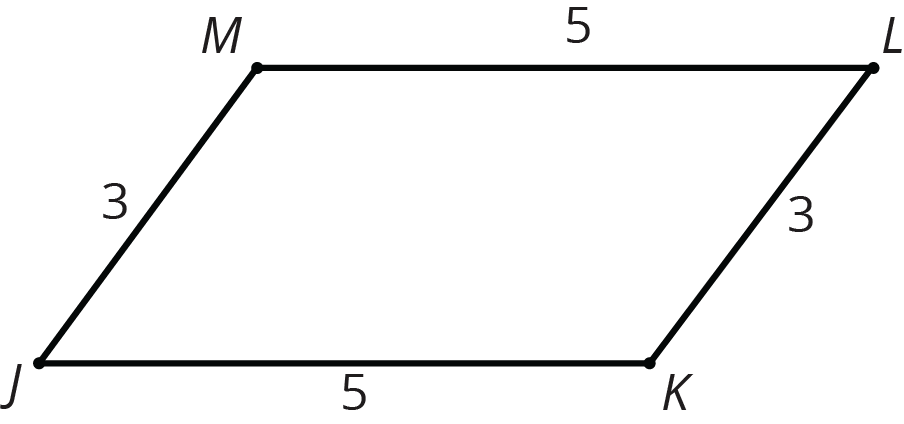
    • If two polygons have the same side lengths, in the same order, but different corresponding angles, the polygons can’t be congruent. For example, parallelogram $JKLM$ can’t be congruent to rectangle $ABCD$. Even though they have the same side lengths in the same order, the angles are different. All angles in $ABCD$ are right angles. In $JKLM$, angles $J$ and $L$ are less than 90 degrees and angles $K$ and $M$ are more than 90 degrees.

Practice Problems ▶